Перевод систем счисления

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

ПЕРЕВОД ЧИСЕЛ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ.

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.

Например, требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 2:

101101102 = (1·27)+(0·26)+(1·25)+(1·24)+(0·23)+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210

Двоичная система счисления для использования вне компьютера очень громоздка.
Для сокращения записи двоичных чисел используют систему счисления с основанием 16. Для изображения чисел в шестнадцатеричной позиционной системе счисления требуется шестнадцать цифр. Первые десять цифр позаимствованы из десятичной системы счисления. Для обозначения шести недостающих цифр используются первые буквы латинского алфавита: A, B, C, D, E ,F. Цифры шестнадцатеричной системы счисления:

1 ,2 , 3, 4 , 5 , 6 , 7 , 8, 9 , А , B ,C , D , E , F .

Двоичные числа переводим в шестнадцатеричную систему по таблице, представленной выше, следующим образом:
а) двоичное число разбивается на группы по четыре цифры влево и вправо от запятой; неполные группы дополняются нулями;
б) каждая группа заменяется соответствующими шестнадцатеричными цифрами по таблице.
1001.01012 =9.516

ПЕРЕВОД ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ В ДВОИЧНУЮ

Для перевода чисел из десятичной системы счисления в двоичную используют так называемый "алгоритм замещения", состоящий из следующей последовательности действий:

  1. Делим десятичное число А на 2. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит двоичного числа.
  2. Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток (0 или 1) записывается в разряды двоичного числа в направлении от младшего бита к старшему.
  3. Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a = 1.

 

Например, требуется перевести десятичное число 247 в двоичное. В соответствии с приведенным алгоритмом получим:

24710 : 2 = 12310
24710 - 24610 = 1, остаток 1 записываем в конец двоичного числа.
12310 : 2 = 6110
12310 - 12210 = 1, остаток 1 записываем впереди предыдущего двоичного числа.
6110 : 2 = 3010
6110 - 6010 = 1, остаток 1 записываем в старший разряд двоичного числа.
3010 : 2 = 1510
3010 - 3010 = 0, остаток 0 записываем в старший разряд двоичного числа.
1510 : 2 = 710
1510 - 1410 = 1, остаток 1 записываем в старший разряд двоичного числа.
710 : 2 = 310
710 - 610 = 1, остаток 1 записываем в старший разряд двоичного числа.
310 : 2 = 110
310 - 210 = 1, остаток 1 записываем в старший разряд двоичного числа.
110 : 2 = 010, остаток 1 записываем в старший разряд двоичного числа.

Таким образом, искомое двоичное число равно 111101112.

Запись перевода в виде столбика:

Перевести число 11 из десятичной системы счисления в двоичную систему.

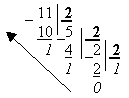Соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы, и получим число в двоичной системе счисления:

1110 = 10112

Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.

Пример.

а) Перевести 305.48 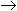"2" с.с.

б) Перевести 7B2.E16 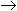"2" с.с.

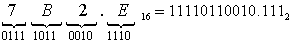
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.

Таблица 1

ТАБЛИЦА СООТВЕТСТВИЯ ПЕРВЫХ 17 ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ ОСНОВНЫХ СИСТЕМ СЧИСЛЕНИЯ

Двоичная система Восьмеричная система Десятичная система Шестнадцатеричная система
0 0 0 0
1 1 1 1
10 2 2 2
11 3 3 3
100 4 4 4
101 5 5 5
110 6 6 6
111 7 7 7
1000 10 8 8
1001 11 9 9
1010 12 10 A
1011 13 11 B
1100 14 12 C
1101 15 13 D
1110 16 14 E
1111 17 15 F
10000 20 16 10

Пример.

а) Перевести 1101111001.11012 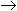"8" с.с.

б) Перевести 11111111011.1001112 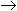"16" с.с.

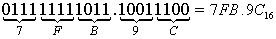
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

Оформить в текстовом редакторе Word и проверять в программе калькулятор и он-лайн калькуляторах

  1. Переведите в двоичную систему десятичные числа:
  1. 123,
  2. 45,
  3. 99,
  4. 456,
  5. 1024,
  1. Запишите двоичные числа в порядке возрастания:

10, 10101, 10100, 11, 10001.

  1. Проверьте равенства:
  1. 1112 = 710
  2. 101102 = 2210
  3. 10101012 = 8510.
  1. Переведите из одной системы счисления в другую
  1. 3058 ® ?2
  2. 7D216 ® ?2
  3. 111011002 ® ?8
  4. 101111100012 ® ? 16
  1. Сложить числа в двоичной системе и перевести в шестнадцатеричную (выполнить только в программе калькулятор)
  1. 1100112 + 1110002 ® ? 16
  2. 1011112 + 1111012® ?8