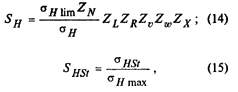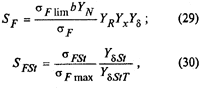1. Контактное напряжение в полосе зацепления
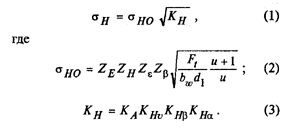
2. Допускаемое контактное напряжение, не вызывающее опасной Контактной усталости материала
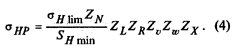
3. Допускаемое предельное контактное напряжение, не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя:
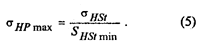101. Нагрузочная способность поверхностей зубьев
| Критерий | Условия нагрузочной способности |
| Напряжение |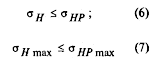 
|
| Безопасность |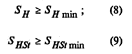 
|
| Ресурс |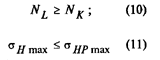 
|
| Вероятность безотказной работы |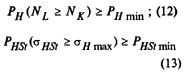 
|
| Примечание.
где σH max - максимальное контактное напряжение за весь срок службы; SHI - расчетный коэффициент запаса | |
24. Расчет зубьев на прочность при изгибе.
При расчете определяется напряжение изгиба σF в опасном сечении на переходной поверхности.
1. Напряжение изгиба в опасном сечении
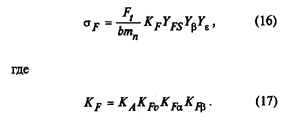
2. Допускаемое напряжение изгиба на переходной поверхности зуба, не вызывающее усталостного разрушения материала:
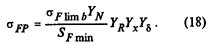
3. Допускаемое напряжение изгиба в опасном сечении, не вызывающее остаточных деформаций, хрупкого излома или первичных трещин
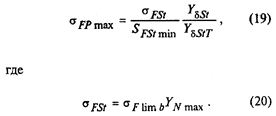
Нагрузочная способность зуба при изгибе обеспечивается при выполнении условий любого критерия по табл. 102.
Ниже изложен пример расчета на прочность зубчатой передачи, базирующийся на основных расчетных зависимостях (1)-(30).
102. Нагрузочная способность зуба при изгибе
| Критерии | Условия нагрузочной способности |
| Напряжение |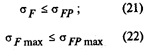 
|
| Безопасность |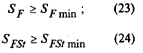 
|
| Ресурс |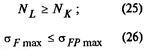 
|
| Вероятность безотказной работы |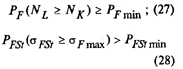 
|
| Примечание.
где σF max - максимальное местное напряжение изгиба в опасном сечении зуба за весь срок службы; | |
25. 3 Силы, действующие в прямозубой передачи, и давление на опоры
Под действием внешних моментов приложенных к зубчатому колесу между зубьями возникают сильные взаимодействия. При этом полное давление на зуб можно разделить на две взаимоперпендикулярные составляющие силы: силу F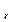 
- называют окружной, она направлена по касательной к начальной окружности и составляющая, которая направлена перпендикулярно к оси вращения и называется распорной силой.
, 
, 
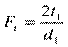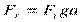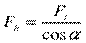. (145)
Для определения сил, действующих в зубчатом зацеплении, используется следующее правило: окружное усилие и полное давление на зуб шестерни направлено в сторону противоположную направлению скорости вращения шестерни. Направление окружности усилия и полного давления на зуб колеса всегда совпадают с направлением скорости вращения этого колеса.
Окружная силаF 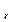вызывает кручение и изгиб вала в горизонтальной плоскости. Распорная сила F 
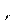вызывает изгиб вала в вертикальной
плоскости. Реакции опор
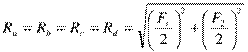
26. Таблица 17. Геометрические параметры прямозубой конической передачи
| Параметр, обозначение | Расчетные формулы |
Внешний окружной модуль 
| 
|
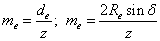
Средний окружной модуль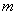 
| 
|
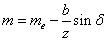
Внешний диаметр вершин зубьев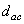 
| 
|
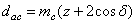
Внешний делительный диаметр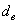 
| 
|
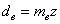
Внешний диаметр впадин зубьев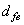 
| 
|
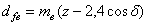
Высота зуба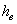 
| 
|
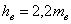
Высота головки зуба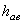 
| 
|
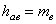
Высота ножки зуба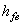 
| 
|
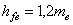
Окружной шаг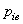 
| 
|
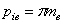
Окружная толщина зуба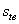 
| 
|
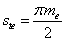
Окружная ширина впадины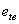 
| 
|
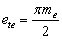
Радиальный зазор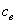 
| 
|
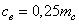
Ширина зубчатого венца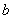 
| 
|
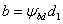
Внешнее делительное конусное расстояние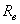 
| 
|
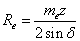
Угол делительного конуса шестерни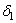 
| 
|
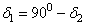
колеса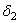 
| 
|
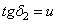
27. С учетом геометрических соотношений в конической передаче по нормали к зубу действует сила Fn1 (рис. 54). Эту силу разложим на две составляющие: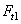 
и 
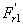. В свою очередь 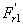разложим на 
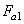и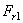 
. Запишем:
; 
; 
.
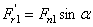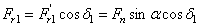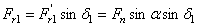Осевая сила на шестерне численно равна радиальной силе на колес
31. С целью повышения несущей способности зубчатых передач М.Л.Новиков [1] разработал новый способ образования сопряженных поверхностей для различных видов зубчатых передач с параллельными, пересекающимися и перекрещивающимися осями. До Новикова исходили из того, что в передачах с параллельными осями поверхности зубьев находятся в линейном контакте, а их торцевые профили являются взаимоогибаемыми кривыми. Новиков предложил перейти от линейного контакта поверхностей к точечному. При этом профили зубьев в торцевом сечении могут быть не взаимоогибаемыми кривыми и их можно выполнять как выпуклый и вогнутый профили с малой разностью кривизн. В передаче с параллельными осями линия зацепления является прямой линией параллельной осям колес. Зацепление Новикова имеет только осевое перекрытие :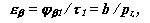 
где b - ширина зубчатого венца, pz - осевой шаг. Поэтому поверхности зубьев выполняются винтовыми (косозубыми) с углом подъема винтовой линии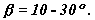 
Одним из основных параметров зацепления Новикова является расстояние от полюса зацепления Р до точки контакта К, которое определяет положение линии зацепления ( прямой К-К параллельной осям вращения и проходящей через точку контакта К ) относительно оси мгновенного относительного вращения Р-Р. Согласно рекомендациям работы [ 14.1 ], это расстояние выбирается в зависимости от величины передаваемой мощности в пределах
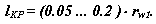
Радиусы кривизны рабочих участков профилей рекомендуется выбирать для выпуклой поверхности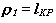 
,для вогнутой поверхности 
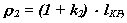, где k2 = 0.03 ... 0.1 .
Радиус окружности вершин колеса с выпуклыми зубьями:
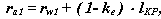где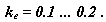 
Дуги рабочих профилей выпуклых зубьев проводят от начальной окружности до окружности вершин. Радиус окружности вершин колеса с вогнутыми зубьями .
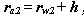где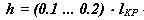 
- глубина захода зубьев.
Радиус окружности впадин колеса с выпуклыми зубьями:
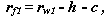
где c - радиальный зазор, приблизительно равный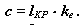 
Радиус окружности впадин колеса с вогнутыми зубьями :
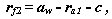где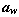 
- межосевое расстояние в передаче .
Преимущества зубчатых передач с зацеплением Новикова:
- повышенная контактная прочность зубьев, за счет использования зацепления вогнутого профиля с выпуклым ( приведенный радиус кривизны определяется суммой радиусов кривизны профилей );
- перекрытие в передачах Новикова обеспечивается только за счет осевого перекрытия, поэтому высота зубьев может быть достаточно малой, что обеспечивает высокую изгибную прочность зубьев ( в целом, по приблизительным оценкам, нагрузочная способность передач Новикова в 2-3 раза выше, чем косозубых эвольвентных передач с одинаковыми размерами);
- точечное зацепление (пятиподвижная кинематическая пара) обеспечивает в передачах с зацеплением Новикова меньшую чувствительность к монтажным погрешностям.
К недостаткам передач Новикова можно отнести
- более сложную технологию изготовления, за счет использования инструмента с профилями криволинейной конфигурации;
- наличие значительных осевых нагрузок на подшипники из-за использования винтовых зубьев с большими углами подъема винтовой линии;
- склонность зубьев винтовых колес к излому у торца при входе в зацепление
28. Расчет на контактную прочность
Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же как у эквивалентного цилиндрического. Эквивалентным колесом называется такое цилиндрическое колесо, у которого делительный диаметр и модуль равны делительному диаметру и модулю в среднем нормальном сечении реального конического колеса рис.2.3.20.
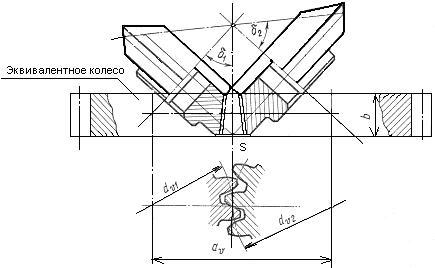
Рисунок 2.3.20 Схема построения эквивалентного колеса
Межосевое расстояние эквивалентной передачи
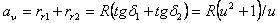(2.3.61)
Передаточное число эквивалентной передачи
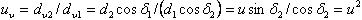(2.3.62)
Момент на эквивалентном колесе
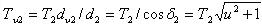(2.3.63)
29. Расчет конических зубчатых передач на изгиб
Формула проверочного расчёта конических прямозубых передач:
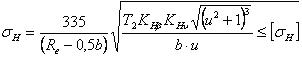(2.3.64)
Формула проектировочного расчёта конических прямозубых передач:
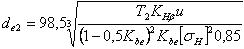(2.3.65)
Условие прочности
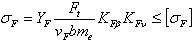(2.3.66)
где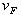 
- коэффициент вида конических колёс. Для прямозубых колёс 
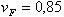; для колёс с круговыми зубьям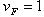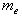и 
; 
и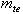 
- внешний и окружёной модули; YF – коэффициент формы зуба. Внешний окружной модуль 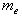или 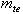определяют расчётом на изгиб по формуле
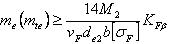(2.3.67)
Минимальное число зубьев шестерни z конической передачи с круговыми зубьями определяют по формуле
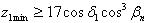(2.3.68)
30. Гипоидные передачи рекомендуется применять в тех случаях, когда требуется повышенная плавность передачи вращения, как например, в приводах заднего моста легковых автомобилей. Гипоидные зубчатые колеса могут работать с такими же окружными скоростями, как спиральнозубые конические колеса. Кроме того, гипоидные передачи целесообразно применять в передачах с большим передаточным числом, где существенно повышение прочности шестерни (пример — передачи грузовых автомобилей), а также в передачах, где по конструктивным соображениям требуется вывести оба вала за пределы передачи.
Конические и гипоидные пары можно применять как в понижающих, так и в повышающих передачах. В последнем случае не рекомендуется применять пары с передаточным числом больше 3:1, причем шестерню необходимо монтировать на подшипниках качения во избежание заклинивания. Применение подшипников качения рекомендуется для всех конических и в особенности спиральнозубых и гипоидных передач.
Общие указания по проектированию конических зубчатых колес. Износоустойчивость конических зубчатых колес повышается с увеличением числа зубьев; однако при проектировании передач следует иметь в виду, что при большом числе зубьев их профили имеют малую кривизну. Если кривизна профилей зубьев у обоих сцепляющихся зубчатых колес мала, то при самых небольших погрешностях изготовления контакт зубьев будет выходить на кромку, вызывая повышенный шум при их работе. Число зубьев шестерни целесообразно определять по эмпирической формуле, действительной для закаленных зубчатых колес, сцепляющихся под углом 90°:
zш=К√1+0,01(1—0,64 lg i)(dш/К)2,
где
К =22 cos2 β —9 lg i+16/i sin2 β
Если зубчатые колеса подвергаются притирке, то настоятельно рекомендуется, чтобы число зубьев шестерни и число зубьев колеса были взаимно простыми, т. е. не имели общих множителей. При этом качество притирки зубьев после закалки значительно улучшается.
Прецизионные зубчатые колеса, от которых требуется высокая точность передачи движения, следует выполнять либо незакаленными, либо закаленными и шлифованными. Прецизионные передачи должны иметь кратное передаточное отношение, например 1, 2, 3 и т. д. Точное изготовление пары с передаточным отношением 3:2; 4:5; 5:3 и т. д. затруднительнее.
При существующих методах расчета конических зубчатых колес прочность их зубьев принимается пропорциональной ширине зубчатого венца; поэтому конструкторы, не имеющие большого опыта в проектировании конических передач, часто стремятся чрезмерно увеличивать длину зубьев. Это не приводит к желаемым результатам, так как при большой ширине венца зубья на узком конце становятся слабыми и в случае, если нагрузка сосредоточивается в этом месте, передача быстро выходит из строя. Ввиду сказанного рекомендуется проектировать зубчатые колеса так, чтобы ширина зубчатого венца была не более 0,3 длины образующей делительного конуса.
Спиральнозубые конические и гипоидные колеса могут иметь правое или левое направление спирали. Сцепляющиеся зубчатые колеса имеют различное направление спирали. Пара сцепляющихся зубчатых колес считается парой правого направления, если шестерня имеет правую спираль, или парой левого направления, если шестерня левоспиральная. Зубчатое колесо называется правоспиральным, если при рассмотрении его со стороны вершины конуса зубья наклонены наружу в сторону движения часовой стрелки; если же они наклонены в противоположную сторону, то зубчатое колесо называется левоспиральным. Зубья зерол-колес условно называются правыми, если они обращены вогнутыми сторонами в сторону вращения часовой стрелки, и левыми — при противоположном направлении. Правоспиральная шестерня, вращаясь по часовой стрелке (если смотреть со стороны вершины конуса) стремится переместиться в направлении от вершины конуса, а левоспиральная — к вершине конуса. Если при этом шестерня может иметь чрезмерную осевую игру, то зубья могут сблизиться до плотного зацепления и произойдет заклинивание. Поэтому в реверсивных передачах необходимо обращать особое внимание на конструкцию и качество сборки подшипников, удерживающих шестерню (или колесо) от осевого смещения. При нереверсивных передачах целесообразно выбирать направление спирали таким, чтобы осевое давление было направлено в сторону от вершины начального конуса; при этом осевое смещение зубчатых колес вызывает лишь увеличение зазора в зацеплении.
Качество конических зубчатых колес в значительной степени зависит от их конструкции, которая должна учитывать технологические факторы, а также обеспечивать достаточную жесткость. Ниже приводятся практические рекомендации и указания, которыми следует руководствоваться при проектировании передач.
Колеса и шестерни должны иметь опорный торец достаточных размеров, служащий базой при их обработке и монтаже. Расстояние Ам ( (фиг. 26, а и б) от вершины конуса до опорного торца (монтажная дистанция) должно указываться в чертежах с допуском.