Температурная деформация
Температурные деформации (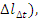 
вызванные изменением температуры детали можно определить по формуле:
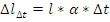
l – размер детали.
α – коэффициент линейного расширения детали.
∆t – перепад температур детали.
Особенно чувствительны к температурным деформациям такие приборы как: телескопы, измерительные машины, теодалиты, ганиометры.
В установившемся тепловом режиме возможны два варианта распределения температуры: 1. постоянна температура, 2. постоянен градиент температуры. Расчёт температурной деформации возможен в обоих случаях. Расчёт температурных деформаций не возможен при неустановившемся тепловом режиме. Тогда задачей конструктора является сведение к минимуму влияния температуры на точность прибора. Этого можно добиться следующими способами: подбор материалов с близкими коэффициентами линейного расширения, оградить детали и весь прибор от температурного влияния окружающей среды (теплоизоляция, термостатирование, экранизация, применение конструктивных температурных компенсаторов).
1 8 . Расчет точности партии однородных измерительных устройств
При расчете точности партии изготавливаемых измерительных устройств имеют дело не с конкретными величинами, или же законами изменения первичных погрешностей, а располагают лишь допусками, ограничивающими предельными значениями возможных первичных отклонений элементов прибора. Очевидно, что при сборке деталей механизма все отклонения размеров годных деталей будут находиться в пределах заданных допусков. То же самое относится к динамическим и температурным погрешностям, ограниченным возможными пределами, а внутри этих пределов они могут иметь любое значение. Так как погрешности, действующие в каждом экземпляре прибора и при определенных условиях его использования могут иметь любые значения, лежащие в пределах допуска, то при расчете точности измерительных устройств следует считать эти погрешности случайными величинами (функциями). Суммирование влияния отдельных погрешностей на результирующую точность прибора не должно исходить из алгебраического сложения действия наибольших возможных отклонений, лежащих в границах допуска. Трудно ожидать столь неблагоприятного одновременного сочетания неточностей. В обычных условиях сборки прибора можно ожидать, что в каждый экземпляр прибора попадут детали с отклонениями, лежащими в разных участках полей допуска. Для учета влияния случайного характера погрешностей звеньев механизма необходимо суммировать действие всех отклонений на основе теории вероятности. Сущность этого метода заключается в учете не только значения отклонения, но и вероятности его появления. Это обстоятельство позволяет не учитывать ряд крайних значений, имеющих малую вероятность появления. Следовательно, использование метода теории вероятности дает значение лучше согласующееся с практически наблюдаемыми величинами, чем те значения, которые были найдены при расчете на возможный максимум - минимум погрешности прибора.
Основная задача технологического точностного анализа - это учет распределения технологических погрешностей в пределах их полей допусков. Эту задачу можно разбить на несколько частных задач:
1. Оценка закона распределения первичных погрешностей.