1 6 .2 Оценка законов распределения технологических первичных погрешностей.
Можно указать 3 способа оценки законов распределения производственных погрешностей, два из которых считаются экспериментальными, а один приближенно-табличным.
1-й способ. Заключается в оценке закона распределения технологической погрешности методом математической статистики в условиях реального производства.
2-й способ. Статистическое исследование финишных операций получения параметров. Базируется на предположении, что финишные операции обеспечивают точность измерительного устройства.
3-й способ. Табличный. Используется в проектном расчете. Заключается в использовании опыта предшествующих поколений.
Значительные работы в этом направлении выполнены профессором Бородачевым, на основе обследования различных технологических приемов обработки деталей и изучении исследований точности производства, проведенных другими технологами. Им схематизированы разные условия производства, которые приведены к 16-ти типам кривых распределения.
Стандартные апроксимации функции распределения случайных составляющих погрешности измерения даны в ГОСТ 8.011. Обычно при ориентировочных расчетах ограничиваются двумя законами:
1. Закон нормального распределения для отклонения размеров (закон Гаусса).
2. Закон распределения существенно положительных величин (отклонения формы и взаимного расположения поверхностей).
1 6 .3 Относительные числовые характеристики распределения первичных погрешностей
Рассмотрим график рассеяния технологических погрешностей изготовления вала с величиной допуска по чертежу равным 2δ. По оси абсцисс отложены погрешности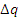 
размера вала, а по оси ординат - плотности вероятности рассеяния этих погрешностей, определенные опытным путем.
f (x)
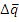
aB
x
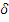δ
Δ0
Смещение центра группирования действительного рассеяния размеров относительно середины поля допуска для наружного размера детали равно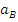 
.
Абсолютные характеристики:
1. 
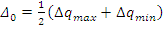
2. 
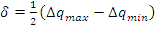
3. 
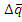
4. 
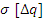
Профессором Бородачевым были предложены относительные характеристики:
5. 
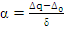- относительная асимметрия
С помощью коэффициента 
Бородачев связал величину смещения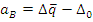 
центра группирования отклонения размера детали относительно середины поля допуска с величиной половины допуска. Этот коэффициент служит для определения величины систематической составляющей погрешности изготовления детали, которая равна .
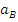6. 
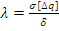- относительное среднее квадратическое отклонение
Оба эти коэффициента α, λ зависят от способа обработки и состояния оборудования, а также от симметричности (несимметричности) рассеяния размеров детали относительно середины поля допуска, т.е. α, λ зависят только от вида закона распределения погрешности.