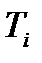14.1 Учет влияния зазора во вращательной паре.
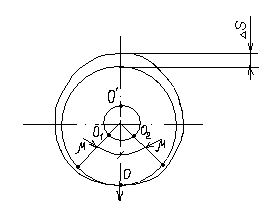При наличии зазора шейка шарнира и отверстия будут располагаться несоосно.
При этом положение подвижного элемента определяется направлением равнодействующей сил, действующих в сочленении.
Равнодействующая сил соответствует реакции шарнира и проходит через точку касания обоих элементов пары. В процессе вращательного движения звена изменяется направление действия реакции и, следовательно, перемещается точка соприкосновения элементов шарнира, т.е. происходит взаимное перекатывание соприкасающихся элементов кинематической пары.
Для каждого мгновенного положения механизма может быть определена действующая погрешность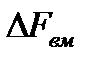 
вдоль выходной линии действия, вызванная смещением оси шарнира в пределах зазора. Эта погрешность определяется:
(*)
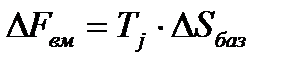где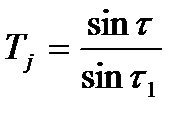 
(**)
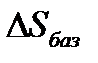- действующее смещение идеального центра вращения;
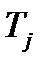- коэффициент влияния смещения центра;
, 
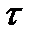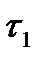- находятся из схемы преобразованного механизма.
Формулы (*) и (**) являются универсальными при сохранении требований к дефектному перемещению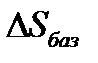 
и расстановке углов 
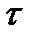и 
.
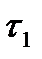Смещение идеального центра вращения направляющей следует рассматривать для трех видов вращательных направляющих:
1) на опорах скольжения;
2) на опорах качения;
3) на упругих опорах.
Для опор скольжения характерным является смещение идеального центра цапфы из центрального положения относительно отверстия на размер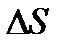 
/2, где 
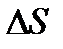- зазор по направлению действующей реакции.
Если при реверсировании работы механизма направление действия реакции отклоняется из-за сил трения на угол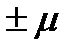 
, то вызываемая этим реакция перемещения центра будет определяться:
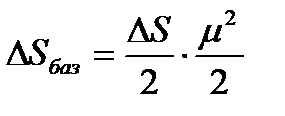
В наихудшем случае, когда не будет иметь место перекатывание (скатывание) центра цапфы из точки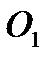 
в точку 
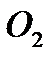, а при реверсировании механизма центр цапфы будет переходить из точки 
в диаметрально противоположную точку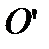 
. При этом проекция перемещения центра цапфы равна величине полного зазора:
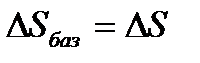
При вращательных направляющих, выполненных на опорах качения, следует принимать во внимание как размер радиального зазора в подшипниках качения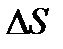 
, так и размер радиального биения Е наружного кольца относительно внутреннего. В этом случае размер перемещения звеньев:
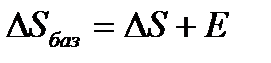
Для вращательных направляющих, выполненных на упругих опорах, следует также учитывать проекции смещения центра поворота в процессе движения звена. При этом можно воспользоваться исследованиями А.Т.Драудина, в которых получены следующие результаты:
- для одиночной плоской пружины
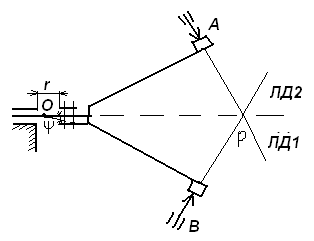
При базовой линии, направленной вдоль оси пружины, проекция смещения идеального центра О при повороте на угол ψ от нейтрального положения определяется:
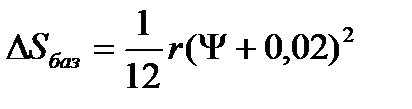
где r – длина свободного участка пружины.
- для крестообразного упругого шарнира
При базовой линии, направленной вдоль оси продольной симметрии, проекция смещения центра на ось продольной симметрии (базовую ось)
, 
,
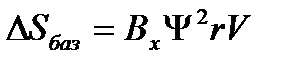
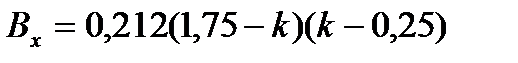
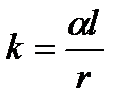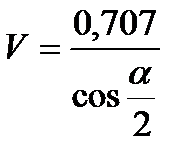l – большее расстояние от центра О до заделки.
Пр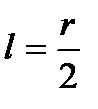и 
и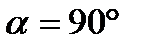 
k=1, V=1, следовательно:
,
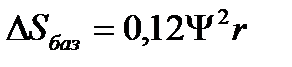где ψ – угол отклонения от нейтрального положения.
14.2 Учет влияния погрешностей прямолинейных направляющих.
При рассмотрении поступательного движения направляемого звена механизма возможны два случая:
1) линии действия рабочих точек направляемого звена пересекаются в точке Р.
2) линии действия рабочих точек звена параллельны между собой.
1 случай: линии действия пересекаются.
В случае, когда линии действия пересекаются в точке Р, особенности рассмотрения проявления погрешностей для поступательных направляющих связаны с тем, что центр мгновенного поворота точка О удален в бесконечность, и базовая линия Р-Р проходит через точку Р, перпендикулярно к траектории идеального движения.
С учетом этой особенности могут быть использованы для расчета ранее рассмотренные формулы:
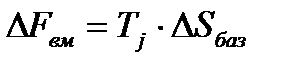
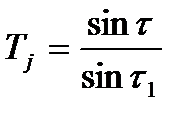
Здесь под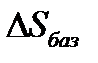 
следует понимать погрешность траектории точки Р или любой другой точки, лежащей на нормали Р-Р.
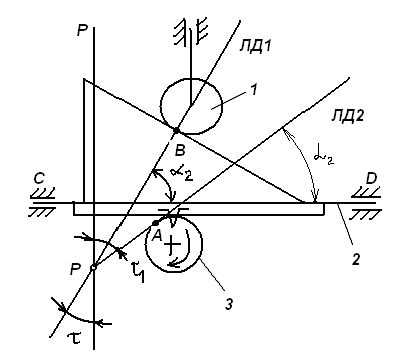
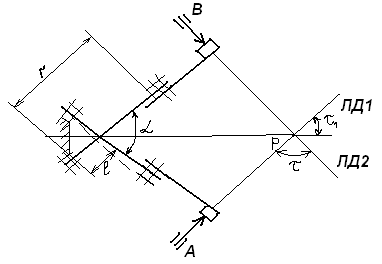
На рисунке показан механизм с поступательно движущимся звеном 2. Это звено снабжено зубчатой рейкой, зацепляющимся в точке А с зубчатым колесом 3, приводящим в движение весь механизм. На звене 2 расположена клиновая линейка, воздействующая в точке В на вертикальный роликовый толкатель 1. Линии действия ЛД1 и ЛД2, проходящие через рабочие точки А и В, пересекаются в точке Р. Базовая линия Р-Р проведена через точку Р, перпендикулярно к траектории движения звена 2.
Погрешности направляющих С и D должны быть приведены к дополнительному перемещению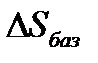 
вдоль линии Р-Р. Перемещения должны учитывать при расчете избыточного приращения по выходной линии ЛД2 по известной формуле:
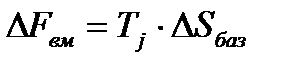
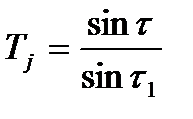
Отметим, что при контроле непрямолинейности хода направляемого звена 2 механизма погрешность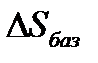 
следует измерять по базовой линии Р-Р.
При расчете погрешности направляющей удобно пользоваться углами, отсчитываемыми между линиями действия и линией движения.
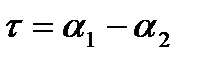
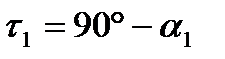
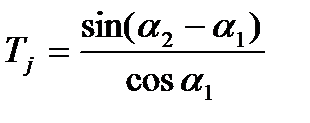
2 случай. Линии действия параллельны.
Если линии действия рабочих точек параллельны, то тогда формула
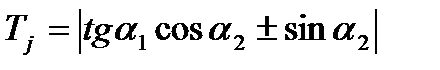
для определения коэффициентов влияния не годна, т.к.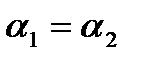 
,следовательно, 
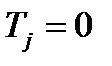Кроме того не может быть применено и понятие о базовой линии, т.к. не только центр поворота удален в бесконечность, как это было в случае прямолинейного поступательного перемещения, но и отсутствует точка пересечения двух линий действия.
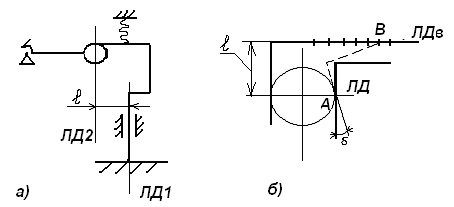
На рис.а показана направляющая для измерительного стержня и рабочей контактной плоскости рычажно-зубчатого индикатора. Рабочая точка А соответствует точке контакта измерительного наконечника с измеряемым изделием, а точка В является точкой соприкосновения плоскости со сферой, закрепленной на качающемся звене рычажного механизма отсчетного прибора.
На рис.б показана направляющая в виде штанги и рамки штангенциркуля. Через рабочую точку А проходит линия действия ЛД, а в точке В расположен отсчетный индекс для снятия отсчета по линейной шкале, с которой совпадает и линия движения ЛДв. Возникающая погрешность на выходе вследствие погрешности направляющей пары связано с возникновением перекоса направляемого звена на угол δ и расстоянием l между линиями действия.
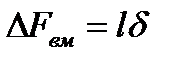
В случае, когда l =0, т.е. линии действия совпадают, имеет место выполнение принципа Аббе, и влияние перекоса направляемого звена становится погрешностью второго порядка малости.
Повышение точности работы поступательных направляющих достигается в некоторых случаях путем разделения транспортных и измерительных функций, выполняемых этими направляющими. Обычно в этих случаях в качестве измерительных направляющих используют образцовые поверхности, разгруженные от усилий, связанных с сопротивлениями перемещения кареток.
15. Сетка влияния конечных погрешностей.
Это совокупность графиков, показывающих изменение всех конечных погрешностей в зависимости от значения входного сигнала, причем графики для всех конечных погрешностей можно построить в одной или в разных координатных сетках, но обязательно в одинаковом масштабе. Значение каждой конечной погрешности подсчитывается при 3-8 значениях входного сигнала.
При построении сетки влияния следует иметь ввиду:
1) на все параметры должны быть назначены допуски, определяемые расчетом по критерию функционирования либо определяемые из конструктивных соображений. При этом величина допуска каждого параметра должна быть принята экономически целесообразной.
2) векторные первичные погрешности учитываются как скалярные, причем направление их действия выбирают самым неблагоприятным образом с точки зрения формирования погрешностей (косинус принимают равным единице – самый худший случай).
3) все первичные погрешности считают симметрично распределенными относительно номинального значения параметра.
4) все первичные погрешности независимы друг от друга.
15.1 Анализ сетки влияния первичных погрешностей.
|
№п/п |
∆i |
| КПi | ||||
| 
| 
| 
| 
| 
| ||
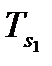
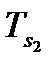
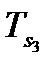
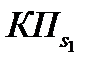
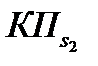
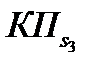
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1) Отыскивается доминирующая погрешность. Под доминирующей погрешностью понимают такую, которая имеет наибольшее абсолютное значение.
2) Сравниваем все остальные погрешности с доминирующей с целью выявления маловлияющих погрешностей.
Если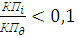 
,то погрешность может быть отнесена к маловлияющей, и можно ее исключить.
Определение ожидаемой суммарной погрешности, т.е. суммирование конечных погрешностей.
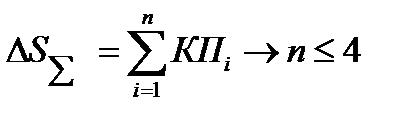
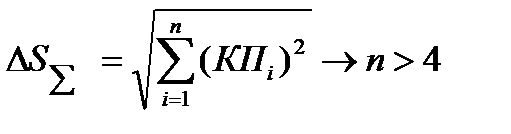
3) Сравнение суммарной ожидаемой погрешности с пределами допускаемой погрешности.