9. Структура теории точности.
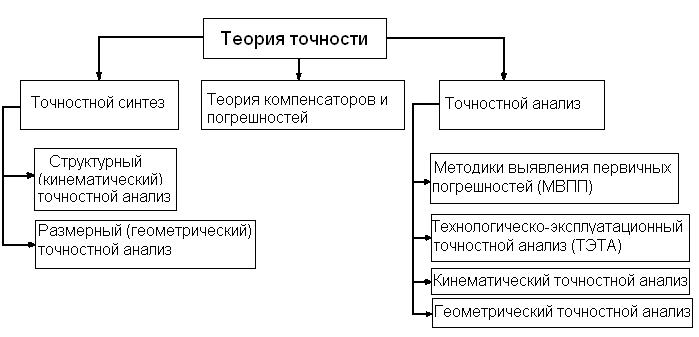
10. Точностной синтез.
Задача: разработка структуры измерительной цепи и выбор номинальных значений параметров этой цепи с целью уменьшения теоретической погрешности.
Известны две разновидности точностного синтеза:
1) структурный точностной синтез (кинематический), задачей которого является разработка структура с наименьшей теоретической погрешностью.
2) размерный (геометрический) точностной синтез, задачей которого является нахождение номинальных значений параметров, минимизирующих теоретическую погрешность.
10.1 Структурный точностной синтез.
Основные положения осуществления:
1) Следует по возможности ограничить число преобразователей информации.
2) Если у нас в измерительной цепи несколько преобразовательных элементов с нелинейной функцией преобразования, то следует эти элементы располагать так, чтобы они хотя бы частично компенсировали нелинейность друг друга.
3) Лучше применять преобразованные элементы с симметричной функцией преобразования.
4) Необходимо грамотно располагать рабочие элементы относительно друг друга.
10.2 Размерный точностной синтез.
С точки зрения минимума погрешности существует 3 категории измерительных устройств:
1) устройства первой категории отличается тем, что они должны иметь минимальную погрешность только при определенных значениях входного сигнала.
2) интегрирующие и суммирующие измерительные устройства, которые накапливают показания. Для этих минимум погрешностей – это минимум накопленной погрешности.
3) все остальные измерительные устройства, у которых при любом значении входного сигнала одинаково неприятна теоретическая погрешность. Для этой категории минимум модуля максимума погрешности:
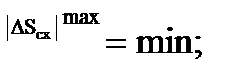
Существует три метода размерного синтеза:
1) метод интерполирования
2) метод квадратичного приближения
3) метод наилучшего равномерного приближения.
10.2.1 Метод интерполирования.
Номинальное значение параметров измерительной цепи отыскиваются из условия равенства нулю теоретической погрешности при определенных значениях входного сигнала, называемых узлами интерполирования.
Пусть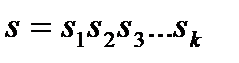 
- узлы интерполирования.
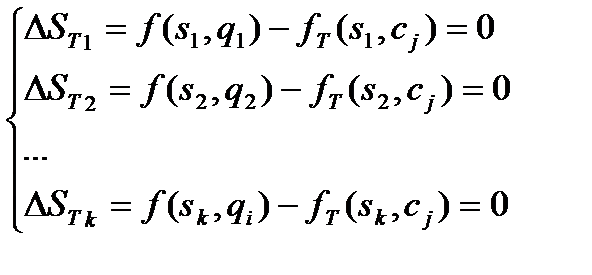
i =1… n
k < n
Имеем систему из k уравнений с n неизвестными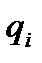 
.
При этом k < n, т.е. имеем статически неопределенную систему. Для синтеза оставляют те значения параметров, которые конструктивно можно реализовать регулируемыми (легко поддается регулировке).
10.2.2 Метод квадратичного приближения.
Номинальное значение параметров измерительной цепи выбирают из условия минимальности средней квадратической погрешности.
; 
;... 
.
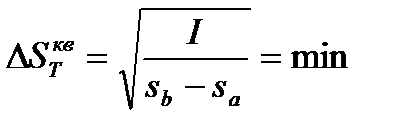
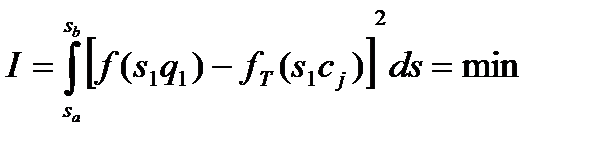
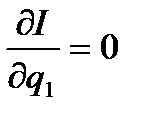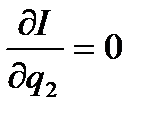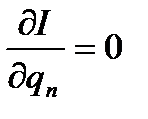Многочлен степени n, который по сравнению с другими многочленами этой степени имеет наименьшее среднее квадратическое отклонение от 0 – это полином Лежандра типа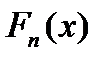 
. Эта функция точно отвечает условию 
=min.
Полученное выражение для определения погрешности схемы приравнивается к полиному и определяют неизвестные параметры.
10.2.3 Метод наилучшего равномерного приближения.
В этом методе параметры измерительной цепи отыскиваются из условия минимальности модуля максимума теоретической погрешности
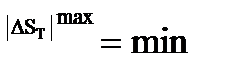
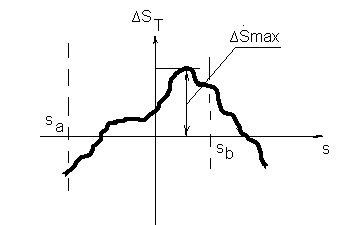
Для решения этой задачи используются специальные полиномы Чебышева, которые на заданном диапазоне аргумента наименее отклоняются от 0.
Наиболее часто используются 3 полинома:
1) 
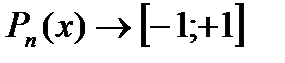
2) 
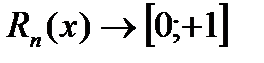
3) 
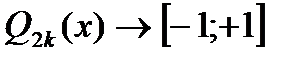
Теоретическую погрешность приравнивают к полиному и решают полученные уравнения.
11. Выявление первичных погрешностей.
Под первичной погрешностью мы понимаем любое отклонение параметров цепи от расчетных, приводящие к искажению градуировочной характеристики.
Принято все первичные погрешности разделять на две категории:
1) скалярные первичные погрешности
2) векторные первичные погрешности.
Скалярные первичные погрешности отличаются тем, что направление их действия нам заранее известно, а значение их заранее предсказать нельзя, но оно может быть принято в пределах допуска.
Векторная первичная погрешность характеризуется неопределенным и непредсказуемым направлением действия. В отличии от скалярной первичной погрешности, векторная является как бы дважды случайной: ее значение – любое в пределах допуска, а направление действия – любое в пределах зоны действия.
Методика рассмотрения первичных погрешностей механизма, предложенная академиком Н.Г.Бруевичем, позволяет строго определить возможное число первичных погрешностей каждого звена и механизма в целом.
11.1 Методика академика Н.Г. Бруевича.
Методика базируется на двух принципах:
1) Принцип независимости действия погрешностей. Первичные погрешности являются взаимонезависимыми, т.е. значение одной погрешности не определяет значений других. Этот принцип позволяет при суммировании погрешностей пользоваться принципом суперпозиции.
2) Принцип координирования, заключается в том, что все первичные погрешности отсчитываются в единой для всего исследуемого механизма системе координат.
По методика Бруевича самая мелкая рабочая часть механизма – элемент кинематической пары. Методика включает в себя 3 пункта:
1) элемент кинематической пары может привнести столько первичных погрешностей, сколько независимых параметров определяют форму, размеры и положение этого элемента в обобщенной системе координат.
2) звено может дать столько первичных погрешностей, сколько дадут вместе все элементы кинематических пар, принадлежащих этому звену.
3) количество первичных погрешностей механизма равно сумме числа первичных погрешностей всех звеньев этого механизма.
Наиболее удобной системой координат по Бруевичу является система координат, связанная с ведомым звеном.
Достоинства:
1.формализована
2.методика позволяет найти и учесть все первичные погрешности
Недостатки:
1.методика всегда дает громадное число первичных погрешностей, и простота методики в поиске погрешностей вырождается в очень сложный анализ
2.методика дает возможность выявлять лишь погрешности размеров и погрешности взаимного расположения при игнорировании погрешностей формы.
Методика выявления первичных погрешностей рекомендуется при исследовании механизмов приборов имеющих простые формы элементов кинематических пар: плоскости, сферы, точки цилиндра. В подобных случаях форма элементов может быть выявлена с высокой точностью, и ее изменения не могут заметно отразиться на работе прибора, особенно в динамическом режиме и, следовательно, не возникает необходимости в установлении связи между отклонениями формы кинематических элементов и погрешностями процесса образования этих поверхностей.
11.2 Методика профессора Н.А. Калашникова.
Действующей погрешностью кинематической пары называется погрешность размеров или формы элементов пары, непосредственно проявляющаяся в работе. Понятие действующей погрешности, введенное профессором Калашниковым, является основой разработанной им теории реальных механизмов.
В высших кинематических парах, ввиду последовательного сопряжения поверхностей, должна рассматриваться непрерывно действующая погрешность.
| φ |
ΔFk
ΔFБ
ЛД
Для нахождения значения и характера изменения действующей погрешности необходимо учитывать, что взаимодействие между профилями элементов кинематической пары находят по линии действия, проходящей в каждый момент через точку взаимодействия элементов и совпадающей с направлением рабочего усилия. Для действующей погрешности характерно то, что она является комплексной, т.е. погрешностью, отражающей суммарное действие всех погрешностей звена. Комплексную действующую погрешность не следует понимать как полученную в результате суммирования отдельных первичных погрешностей. Наоборот, первичные погрешности должны рассматриваться как частные погрешности общей функциональной погрешности звена, на которые ее раскладывают.
Данная методика наиболее эффективна применительно к сложным поверхностям, получаемых кинематическим путем (кулачки, зубчатые колеса, ходовые винты и т.д.).
12. Методы отыскания коэффициентов влияния и конечных погрешностей
Коэффициент влияния – это отношение изменения сигнала на выходе измерительного устройства к вызывающей его первичной погрешности.
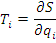
12.1.Метод дифференциальный.
Часто применяют для определения влияния различных составляющих величин на выходной сигнал, математически выраженный через величины, входящие в передаточную функцию.
Коэффициент влияния отыскивается как частная производная градуировочной характеристики идеальной измерительной цепи по соответствующему параметру.
;
;
;
;
;
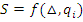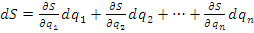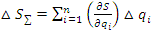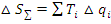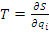Сущность дифференциального метода заключается в том, что составляются уравнения механизма, т.е. уравнения положения или перемещения ведомого звена в зависимости от координаты ведущего звена; затем дифференцированием его в частных производных, и полученный полный дифференциал есть ошибка положения или перемещения механизма.
Коэффициент влияния определяет долю влияния конкретной погрешности на суммарную.
Достоинства метода:
1.Метод является универсальным, т.е. пригоден для исследования измерительных цепей, составленных из любых преобразовательных элементов.
2.Может быть использован при исследовании группы однородных механизмов.
3.Является самым точным
Недостатки метода:
1.Требует знания градуировочной характеристики
2.С помощью метода нельзя отыскать коэффициент влияния нулевых параметров.
Указанные недостатки дифференциального метода ограничивают его применение при исследовании измерительных устройств, в которых существенное значение имеют погрешности формы кинематических элементов, их взаимное положение, т.е. те факторы, которые формируют нулевые параметры.
12.2 Метод преобразованной цепи.
Этот метод совместно с методикой рассмотрения первичных погрешностей является основой теории точности механизмов, разработанной академиком Н.Г. Бруевичем.
Метод позволяет графически, графоаналитически, аналитически находить коэффициенты влияния первичных погрешностей по всем параметрам механизма, минуя отыскание функции положения механизма.
- По Бруевичу коэффициент влияния первичной погрешности отыскивается как передаточное отношение преобразованного механизма.
- Преобразованным называется механизм с точно выполненными звеньями, у которого ведущие звенья закреплены (т.е. неподвижны), а звенья, имеющие погрешность, преобразованы в ведущие, с направлением движения, совпадающим с направлением рассматриваемой первичной погрешности.
Достоинства метода:
1.Универсален
2.Не нужна градуировочная характеристика