18.2 Последовательность расчета точности партии однородных измерительных устройств….40
19.Компенсация погрешностей механизма………………………………………………………..41
19.1. Виды конечных погрешностей механизма…………………………………………………..41
19.2. Классификация погрешностей по закономерности их изменения и по способам регулировки…………………………………………………………………………………………42
19.2.1 Погрешности постоянные (аддетивные)…………………………………………………..43
19.2.2 Прогрессивные (мультипликативные). ……………………………………………………43
19.2.3 Нелинейные…………………………………………………………………………………..43
19.2.4 Погрешности периодические……………………………………………………………….44
19.2.5 Апериодические …………………………………………………………………………….44
Литература…………………………………………………………………………………………..46
1. Предмет и задачи курса
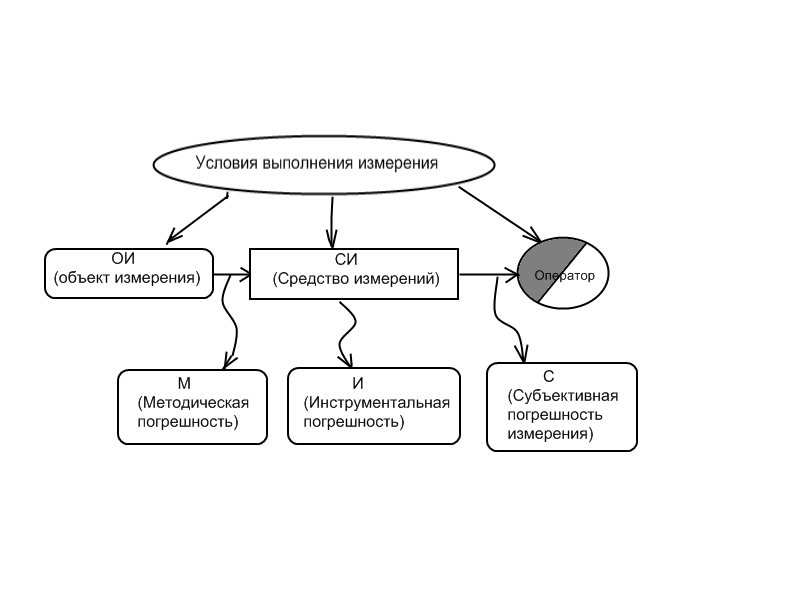
Суммарная погрешность измерения может быть представлена в следующем виде:
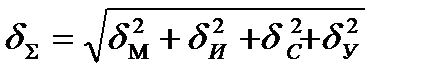
где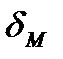 
- методическая составляющая,
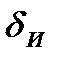- инструментальная составляющая,
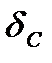- субъективная составляющая,
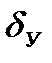- погрешность, связанная с отклонением условий измерения от нормальных.
δ𝛴= (1/3…1/5)IT
Погрешность измерения составляет от 1/3 до 1/5 части от допуска на контролируемый параметр.
Предмет теории точности – одна из составляющих суммарной погрешности измерения, а именно инструментальная погрешность. Многообразие направлений рассмотрения точности измерительных устройств, в значительной мере определяющих погрешность измерения, можно отнести к трем стадиям:
1. Проектирование
2. Производство
3. Эксплуатация
На первой стадии осуществляется обеспечение точности, при которой решаются прямая и обратная задачи теории точности.
Задачи теории точности:
1).Прямая (задача синтеза) – выбор структуры устройства, определение номинального значения параметров таким образом, чтобы ожидаемая погрешность не вышла за ранее установленные пределы. 
< [ 
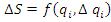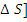
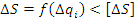
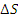- погрешность схемы (теоретическая)
Прямая задача обычно математически выражается одним уравнением точности, содержащим большое число неизвестных, и решается либо методом последовательных приближений, либо путем наложения дополнительных условий. С использованием вычислительной техники задача решается методом статистических испытаний, методом Монте-Карло либо методом математического моделирования.
2).Обратная(анализа) –при известной структуре измерительного устройства, известных номинальных значениях параметров и допусков на них, необходимо определить ожидаемую погрешность измерительного прибора
а ).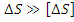 
б).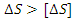 
в).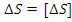 
г).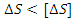 
д).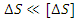 
Эту задачу решают значительно проще, т.к. она сводится к суммированию влияния отдельных составляющих погрешностей и к определению общей выходной неточности, проявляющейся при использовании рассчитываемого измерительного устройства.
Исходя из подобного расчета могут быть сформулированы требования к точности измерительного устройства в целом, на основе которых выполняют контрольно приемочные испытания. В результате расчета могут быть решены вопросы о целесообразности применения метода взаимозаменяемости, о необходимости введения компенсаторов и о выборе регулируемых звеньев.
2. Основные структурные элементы измерительных устройств
Преобразовательный элемент – элемент, обеспечивающий преобразование сигналов измерительной информации. Совокупность преобразовательных элементов, осуществляющих все необходимые преобразования измерительной информации, называется измерительной цепью средства измерения. Часть первого в измерительной цепи преобразовательного элемента, непосредственно воспринимающего сигнал измерительной информации, называется чувствительным элементом.
Преобразовательные элементы могут составлять различные цепи измерительных устройств:
1).Разомкнутые
1.1 с последовательным соединением преобразовательных элементов
|
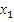
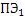
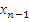s 
|
S
. . .