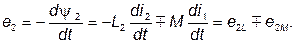2. Настроить цепь в резонанс и записать показания приборов в табл. 10.
3. Увеличить индуктивность катушки примерно на 10 % по сравнению с резонансной. Записать показания приборов в табл. 10.
4. Уменьшить индуктивность катушки примерно на 10 % по сравнению с резонансной. Записать показания приборов в табл. 10.
5. Для каждого опыта (2, 3, 4) рассчитать все параметры цепи и построить векторные диаграммы. По известным параметрам катушки определить резонансную емкость и сравнить её с данными опыта.
6. Сделать выводы по работе.
Таблица 10 - Результаты лабораторной работы № 6
| Измеренные | Вычисленные | ||||||||||||
| Объект измерения | U, В | I, А | P, Вт | UC, В | UL, В | bC, Ом | gL, Ом | bL, Ом | Y, Ом | cos j | j | C, мкФ | L, Гн |
| L1 | |||||||||||||
| L2 | |||||||||||||
| L3 | |||||||||||||
Контрольные вопросы
1. Как определяется активная, реактивная и полная проводимость ветвей?
2. Что называется активной и реактивной составляющими тока?
3. Треугольник проводимостей, что это такое?
4. Как строятся векторные диаграммы при параллельном соединении ветвей?
6. Что называется резонансом токов?
7. Когда в цепи возможен резонанс токов?
8. Какие интересные явления наблюдаются при резонансе токов?
7. ЛАБОРАТОРНАЯ РАБОТА № 7. Исследование цепи
синусоидального тока со взаимной индуктивностью
Цель работы: экспериментальное определение параметров двух индуктивно связанных катушек, изучение влияния взаимной индуктивности на эквивалентные параметры цепи при согласном и встречном включении катушек.
Теоретическое обоснование
Общие сведения. При рассмотрении цепей синусоидального тока до сих пор учитывалось только явление самоиндукции катушек, обусловленное током в цепи (рис.33).
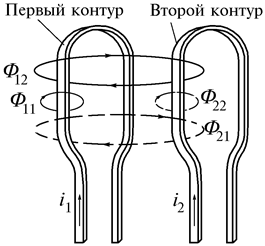
Рис. 33. Контуры со взаимоиндукцией
Цепи, в которых наводятся ЭДС между двумя (и более) взаимно связанными катушками, называются индуктивно связанными цепями. Рассмотрим явление возникновения ЭДС в одном из контуров при изменении тока в другом. Контуры (рис.33) представляют собой плоские тонкие катушки с числами витков 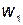 и
и 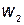 . Поток самоиндукции
. Поток самоиндукции 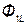 , созданный током
, созданный током 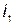 , может быть представлен в виде потока рассеяния
, может быть представлен в виде потока рассеяния 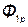 , пронизывающего только первый контур, и потока
, пронизывающего только первый контур, и потока 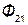 , пронизывающего второй контур:
, пронизывающего второй контур:
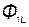 = = 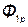 + + 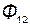 . .
| (58) |
Аналогично определяем поток самоиндукции второго контура:
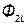 =
= 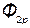 +
+ 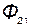 . (59)
. (59)
Потоки 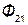 и
и 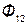 называют потоками взаимной индукции. Их принято обозначать двумя индексами: первый индекс указывает, с каким контуром сцепляется поток, второй – номер тока, вызвавшего данный поток. Например, поток
называют потоками взаимной индукции. Их принято обозначать двумя индексами: первый индекс указывает, с каким контуром сцепляется поток, второй – номер тока, вызвавшего данный поток. Например, поток 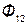 вызван током
вызван током 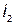 , сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры:
, сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры:
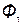 = = 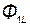 ± ± 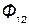 ; ; 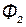 = = 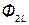 ± ± 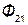 , ,
| (60) |
где «+» - соответствует согласному направлению потоков,
«–» - встречному направлению.
Полные потокосцепления первого и второго контуров:
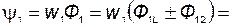 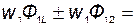 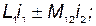
| (61) |
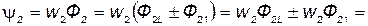 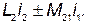
| (62) |
Отношение потокосцепления взаимной индукции в одной цепи к току в другой называется взаимной индуктивностью:
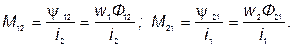
| (63) |
Для линейных электрических цепей всегда выполняется равенство:
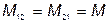 . .
| (64) |
Взаимная индуктивность двух катушек зависит от числа витков, геометрических размеров магнитопровода и взаимного расположения катушек, а также от абсолютной магнитной проницаемости среды (материала магнитопровода). Индуктивную связь двух катушек характеризуют коэффициентом связи:
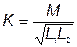 . .
| (65) |
Этот коэффициент всегда меньше единицы, так как магнитный поток взаимной индукции всегда меньше потока самоиндукции и может быть увеличен за счет уменьшения потоков рассеяния бифилярной намоткой катушек (двойным проводом) или применением для магнитопровода материала с высокой абсолютной магнитной проницаемостью.
ЭДС взаимной индукции. ЭДС, индуктируемые в первом и втором контурах, с учетом выражений (64, 63) можно записать в виде:
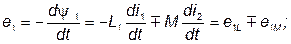
| (66) | ||
|
| (67) | ||
Таким образом, ЭДС каждой катушки определяется алгебраической суммой ЭДС самоиндукции и взаимной индукции. Для определения знака ЭДС взаимной индукции размечают зажимы индуктивно связанных эле-ментов цепи. Два зажима называют одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции складываются. Такие выводы обозначают на схемах одинаковыми условными значками, например, точками или звездочками (рис. 34, а, б).
Одинаково направленные токи 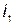 и
и 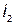 (рис. 34, а) относительно зажимов
(рис. 34, а) относительно зажимов 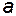 и
и 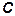 вызывают совпадающие по направлению потоки самоиндукции
вызывают совпадающие по направлению потоки самоиндукции 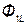 , (
, ( 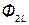 ) и взаимной индукции
) и взаимной индукции 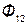 , (
, ( 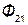 ). Следовательно, зажимы
). Следовательно, зажимы 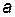 и
и 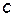 являются одноименными. Одноименной является и другая пара зажимов
являются одноименными. Одноименной является и другая пара зажимов 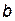 и
и 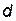 , но условными значками обозначают только одну пару одноименных выводов, например,
, но условными значками обозначают только одну пару одноименных выводов, например, 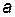 и
и 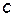 (рис. 34, а). Если токи
(рис. 34, а). Если токи 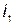 и
и  направлены неодинаково относительно одноименных зажимов (рис. 34, б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.
направлены неодинаково относительно одноименных зажимов (рис. 34, б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.
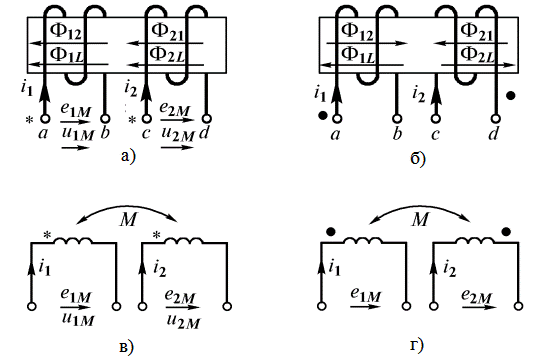
Рис. 34. Само- и взаимоиндукция двух катушек
На схемах магнитопроводы, как правило, не показывают и ограничиваются только обозначением одноименных зажимов (рис. 34, в, г). Одноименные зажимы можно определить опытным путем. Для этого одну из катушек включают в цепь источника постоянного тока, а к другой присоединяют вольтметр постоянного тока. Если в момент подключения источника стрелка измерительного прибора отклоняется, то зажимы индуктивно связанных катушек, подключенные к положительному полюсу источника и положительному зажиму измерительного прибора, являются одноименными.
Определим знаки ЭДС и напряжения взаимной индукции. Допустим, первая катушка (рис. 34, а) разомкнута, а во второй протекает ток  . Выберем положительные направления для
. Выберем положительные направления для  одинаковыми относительно одноименных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда
одинаковыми относительно одноименных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда 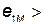 0, потенциал зажима b больше потенциала зажима а, следовательно,
0, потенциал зажима b больше потенциала зажима а, следовательно, 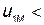 0.
0.
По правилу Ленца знаки 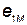 и
и 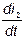 всегда противоположны, поэтому
всегда противоположны, поэтому
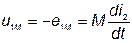 . .
| (68) |
В комплексной форме уравнение имеет вид:
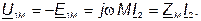
| (69) |
При встречном включении катушек (рис. 34, б)
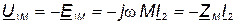 . .
| (70) |
Из выражений (68) и (69) видно, что вектор напряжения на взаимной индуктивности 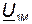 сдвинут по фазе относительно вектора тока
сдвинут по фазе относительно вектора тока 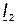 на угол ±90°. Сопротивление
на угол ±90°. Сопротивление 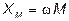 называется сопротивлением взаимной индуктивности, а
называется сопротивлением взаимной индуктивности, а 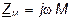 – комплексным сопротивлением взаимной индуктивности. Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».
– комплексным сопротивлением взаимной индуктивности. Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».
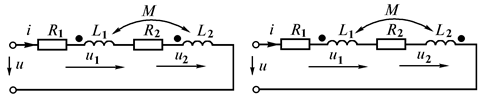
Последовательное соединение двух индуктивно связанных катушек. Рассмотрим две катушки, соединенные последовательно и имеющие активные сопротивления 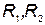 , индуктивности
, индуктивности 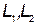 и взаимную индуктивность
и взаимную индуктивность 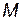 . Возможны два вида их включения – согласное (рис. 35, а) и встречное (рис. 35, б). При согласном включении ток в обеих катушках направлен одинаково относительно одноименных зажимов, поэтому падение напряжения на взаимной индуктивности в уравнениях Кирхгофа для мгновенных значений запишем со знаком «плюс»:
. Возможны два вида их включения – согласное (рис. 35, а) и встречное (рис. 35, б). При согласном включении ток в обеих катушках направлен одинаково относительно одноименных зажимов, поэтому падение напряжения на взаимной индуктивности в уравнениях Кирхгофа для мгновенных значений запишем со знаком «плюс»:
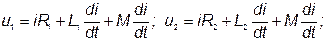
| (71) |
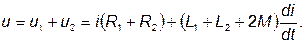
| (72) |
Эти же уравнения в комплексной форме:
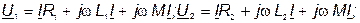
| (73) |
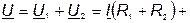 
| (74) |
а) б)
Рис. 35. Согласное (а) и встречное (б) включение катушек
Полное сопротивление цепи при согласном включении:
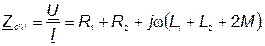
| (75) |
При встречном включении (рис. 35, б) ток в катушках направлен противоположно относительно одноименных зажимов, поэтому напряжения на взаимной индуктивности записывают со знаком «минус». В этом случае уравнения Кирхгофа в комплексной форме имеют вид:
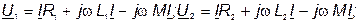
| (76) |
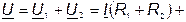 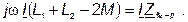
|
Полное сопротивление цепи при встречном включении:
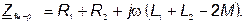
| (77) |
Полное сопротивление цепи при согласном включении больше, чем при встречном. Этим можно пользоваться для определения опытным путем одноименных зажимов индуктивно связанных катушек.
На рис. 36 построены векторные диаграммы для согласного и встречного включения катушек. Начальная фаза вектора тока, являющегося общим для всех элементов цепи, принята равной нулю. По вектору тока сориентированы в порядке записи все слагаемые напряжений 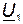 и
и 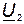 . Упрощает выбор направления векторов правило о том, что умножение комплекса на
. Упрощает выбор направления векторов правило о том, что умножение комплекса на 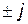 соответствует его повороту на ± 90°. Многоугольники векторов
соответствует его повороту на ± 90°. Многоугольники векторов 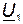 ,
, 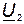 ,
, 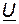 , построенные на диаграмме соответственно с законом Кирхгофа, для наглядности заштрихованы.
, построенные на диаграмме соответственно с законом Кирхгофа, для наглядности заштрихованы.
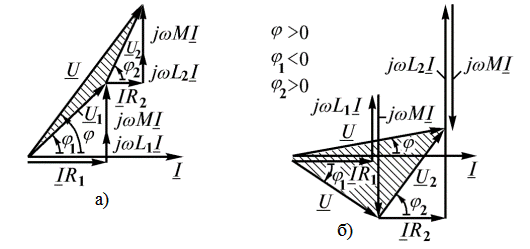
Рис. 36. Векторные диаграммы для согласного и встречного включения катушек
Векторная диаграмма (рис. 36, б) при встречном включении катушек построена в предположении, что 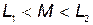 . При таком соотношении параметров в первой катушке наблюдается емкостный эффект, т. к. напряжение
. При таком соотношении параметров в первой катушке наблюдается емкостный эффект, т. к. напряжение 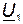 отстает от тока
отстает от тока 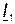 . В цепи нет конденсаторов, но индуктивность первой катушки
. В цепи нет конденсаторов, но индуктивность первой катушки 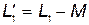 получается отрицательной, что равноценно включению конденсатора. Однако в целом цепь всегда имеет индуктивный характер, т. к. вектор тока отстает от вектора напряжения на входе в виду того, что
получается отрицательной, что равноценно включению конденсатора. Однако в целом цепь всегда имеет индуктивный характер, т. к. вектор тока отстает от вектора напряжения на входе в виду того, что 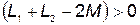 . При согласном включении катушек емкостный эффект невозможен.
. При согласном включении катушек емкостный эффект невозможен.
Экспериментальная часть и порядок выполнения работы
1. Определить параметры двух катушек индуктивности. Для этого собрать схему, показанную на рис. 37. В качестве исследуемых катушек используются цепочки r4-L4 , r5-L5 . Измерить ток, мощность для каждой из 1.
Определить параметры двух катушек индуктивности. Для этого собрать схему, показанную на рис. 6.4. В качестве исследуемых катушек используются цепочки r4-L4 , r5-L5 . Измерить ток, мощность для каждой из катушек, установив на входе цепи такое напряжение, чтобы ток в цепи не превышал 1–2 А. Данные измерений и расчетов занести в табл. 11.
Таблица 11 - Результаты опыта 1
| Катушки | Измерено | Вычислено | |||||||
| U, В | I, А | P, Вт | Z, Ом | R, Ом | ХL, Ом | cos j | j, град | L, Гн | |
| R4-L4 | |||||||||
| R5-L5 | |||||||||
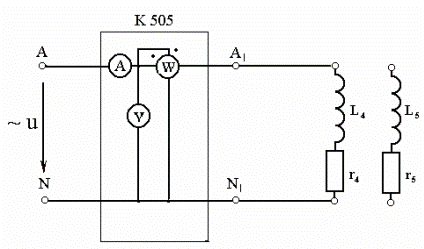
а)
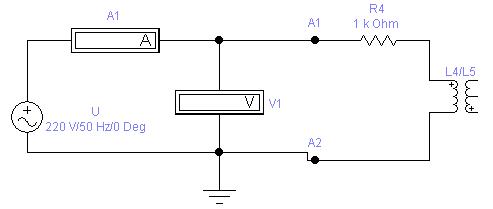
б)
а)- в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 37. Экспериментальная схема опыта 1
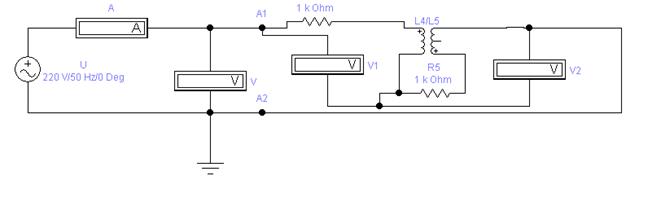
2. Собрать схему рис. 38 для исследования и расчета параметров цепи последовательного соединения индуктивно связанных катушек. Установить заданное преподавателем напряжение на входе цепи и произвести измерения тока, мощности напряжений на каждой катушке. Данные занести в табл. 12. Выключить напряжение. Поменять начало с концом у второй катушки и подать то же самое напряжение, что было в предыдущем опыте. Данные измерений и расчета занести в табл. 12. При согласном включении катушек ток в цепи должен быть меньше, чем при встречном.
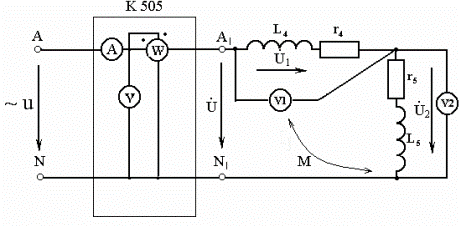
а)
б)
а)- в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 38. Экспериментальная схема опыта 2
Таблица 12 - Результаты опыта 2
| Вид соединения | Измерено | Вычислено | ||||||||||||
| U, В | I, А | P, Вт | U1, В | U2, В | Z, Ом | R, Ом | Хm, Ом | Z1, Ом | Х1m, Ом | Z2, Ом | Х2m, Ом | M. Гн | K | |
| согласное | ||||||||||||||
| встречное | ||||||||||||||
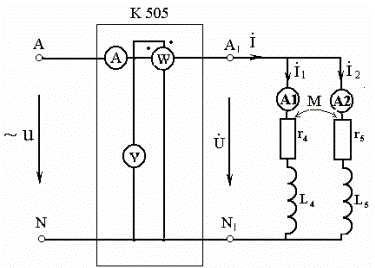
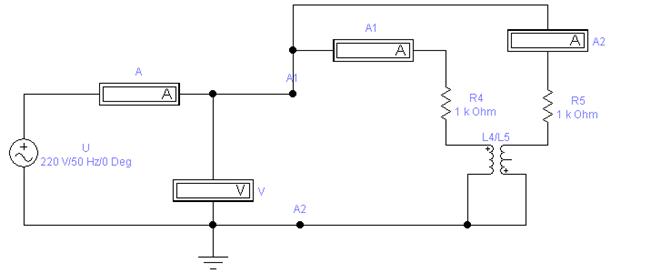
3. Собрать электрическую цепь рис. 39 для исследования и расчета параметров цепи параллельного соединения индуктивно связанных катушек. Установить на входе цепи напряжение, чтобы токи в катушках не превышали 1А. Показания приборов занести в соответствующие графы табл. 13. Выключить напряжение. Поменять начало с концом у второй катушки и подать то же самое напряжение. Данные измерений и расчета занести в табл. 13.
а)
б)
а)- в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 39. Экспериментальная схема опыта 3
Таблица 13 - Результаты опыта 3
| Вид соединения | Измерено | Вычислено | |||||||
| U, В | I, А | P, Вт | I1, В | I2, В | Z, Ом | Z1, Ом | Z2, Ом | j, град | |
| согласное | |||||||||
| встречное | |||||||||