5. Как построить векторные диаграммы при последовательном соединении реактивных элементов?
6. Что называют резонансом напряжений и когда он возможен?
7. Какие интересные явления наблюдаются при резонансе напряжений?
6. ЛАБОРАТОРНАЯ РАБОТА № 6. Исследование цепи
синусоидального тока при параллельном
соединении индуктивной катушки и конденсатора
Цель работы: Исследовать режимы работы разветвленной цепи переменного тока при изменении параметров реактивных элементов; экспериментально исследовать явление резонанса токов, изучить методику построения векторных диаграмм.
Теоретическое обоснование
Рассмотрим цепь из двух параллельных ветвей (рис. 29, а). Допустим, что известны напряжение источника и параметры схемы. Нужно определить
ток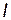 
, потребляемый от источника, и угол сдвига 
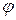на входе цепи.
|
|
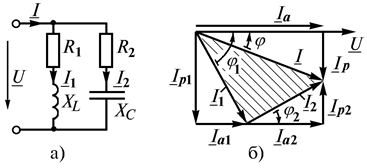
Рис. 29. Параллельное соединение L,C
Для получения расчетных соотношений построим векторную диаграмму токов. Предварительно рассчитаем токи в параллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от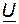 
на угол 
:
 ;  ;  .
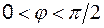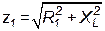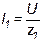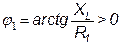| (51) |
У второй ветви характер нагрузки емкостный, вектор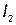 
опережает 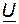на угол 
:
 ;  ;  .
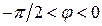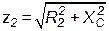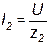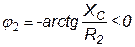| (52) |
В качестве основного вектора принимаем вектор напряжения источника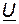 
, являющегося общим для двух параллельных ветвей (рис. 29, б). Тогда относительно него нетрудно сориентировать векторы токов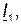 
.
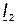При выборе направления тока второй ветви угол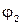 
откладываем от вектора 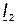в направлении, параллельном вектору 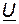, поскольку начала этих векторов не совмещены. В соответствии с первым законом Кирхгофа ( 
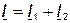) определяем входной ток. В дальнейшем все расчетные соотношения получим из векторной диаграммы. Для этого представим каждый вектор проекциями на взаимноперпендикулярные оси.
Проекцию вектора тока на вектор напряжения назовем активной составляющей тока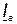 
, а перпендикулярную проекцию – реактивной составляющей 
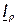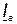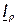. На диаграмме (рис. 29, б) эти составляющие показаны для всех векторов. Составляющие токи и физически не существуют и должны рассматриваться только как расчетные. По диаграмме активная составляющая входного тока определяется как сумма активных составляющих токов в параллельных ветвях:
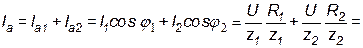
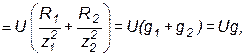
| (53) |
где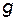 
– активная проводимость цепи, равная арифметической сумме активных проводимостей отдельных ветвей:
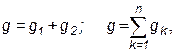
где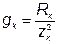 
– активная проводимость 
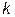- й ветви.
Только в частном случае, когда ветвь представляет собой чисто активное сопротивление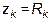 
.
Реактивная составляющая входного тока определяется как алгебраическая сумма реактивных составляющих токов в параллельных ветвях. Реактивную составляющую ветви с катушкой считают положительной, а с конденсатором – отрицательной. Знаки учитывают при подстановке соответствующих значений:
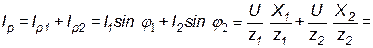
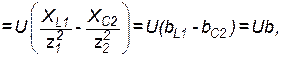
| (54) |
где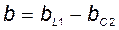 
– реактивная составляющая проводимости цепи, равная алгебраической сумме реактивных проводимостей отдельных ветвей. В общем случае
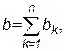
где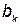 
– реактивная проводимость отдельной 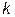-й ветви,
 .
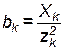| (55) |
Если рассматриваемая ветвь чисто реактивная: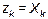 
, проводимость 
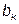является обратной реактивному сопротивлению. Ток на входе цепи (см. векторную диаграмму на рис. 5.1, б) с учетом формул (5.4, 5.5):
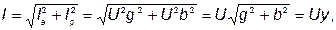
| (56) |
где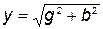 
– полная проводимость цепи, равная геометрической сумме активной и реактивной проводимостей.
Угол сдвига фаз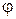 
также определяется из векторной диаграммы. На рис. 30, (а) изображена векторная диаграмма входного тока 
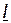, его составляющих 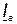и 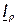и напряжения источника 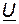. Треугольник, образованный вектором тока и его проекциям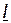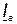и , и 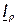, называется треугольником токов (рис. 30, а). Если стороны этого треугольника разделить на напряжение 
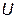, получится треугольник, подобный треугольнику токов – треугольник проводимостей. Он образован проводимостями 
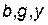, модули которых равны соответствующим проводимостям, а стороны совпадают с векторами 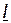, , 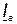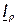треугольника токов (рис. 30, б).
а) б) в)
Рис. 30. Треугольник токов и треугольник проводимостей
На рис. 30 в показан треугольник проводимостей при 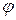<0. Из него находим соотношения между параметрами и формулы для определения угла сдвига фаз:
 ;  ;  ;  ;  ;  .
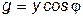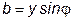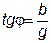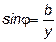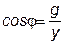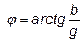| (57) |
Чтобы учесть знак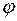 
, следует использовать формулы тангенса и синуса. Когда Ic>IL, т. е. преобладает ток конденсатора, общий ток цепи I является по характеру емкостным и опережает напряжение U на 900 (рис. 31, а). Когда Ic<IL, т. е. преобладает ток катушки, общий ток цепи I является по характеру индуктивным и отстает от напряжения U на 900 (рис. 31, б). Когда же Ic=IL и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис. 31, в). В этой цепи, когда общий ток совпадает по фазе с напряжением, а входная реактивная проводимость 
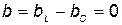или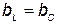 
, может возникнуть явление резонанса. При 
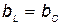противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов.
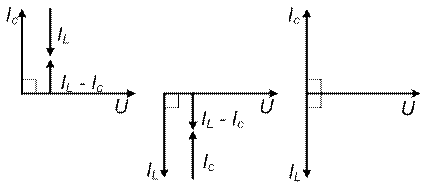
а) б) в)
Рис. 31. Векторные диаграммы токов для случаев: а) Ic>IL; б) Ic<IL; в) Ic=IL
Эти рассуждения приведены в пренебрежении потерями активной мощности в конденсаторе и катушке. При резонансе токов резонансная частота определяется из уравнения
,
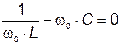откуда так же, как и при резонансе напряжени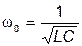й:
и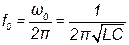 
.
Полная проводимость при резонансе токов оказывается близкой к нулю. Остается некомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи Ic и IL могут превышать его в десятки раз.
Экспериментальная часть
Напряжение на схему подается от лабораторного источника напряжения однофазного переменного тока. Реостат, батарея конденсаторов, индуктивные катушки собираются в схему на стенде при помощи наборной панели. В качестве амперметра, вольтметра используются мультиметры, установленные на стенде. Ваттметр используется настольный. Схема испытаний представлена на рис. 34.
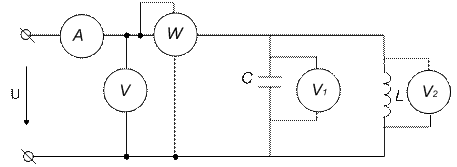
а)
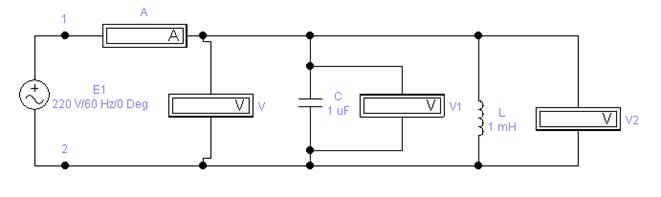
б)
а)- в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 32. Экспериментальная схема
Порядок выполнения работы
1. Собрать схему рис. 5.4 в EWB Движок генератора переменного однофазного тока установить в нулевое положение. Включить схему и установить напряжение на входе цепи.