Цепь, содержащая резистор и конденсатор

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

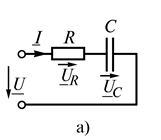
Напряжение на входе цепи (рис. 24, а) согласно второму закону Кирхгофа для действующих значений определяется по уравнению

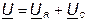. (40)

 

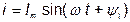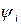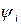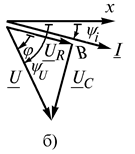
Построим векторную диаграмму, полагая, что в цепи протекает ток и < 0. Вектор тока откладываем под углом к оси 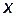в отрица­тельном направлении – по часовой стрелке (рис. 24, б). Вектор напряжения на резисторе 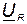совпадает по фазе с вектором тока, а вектор напряжения на конденса­торе 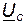отстает от вектора тока на 90°. При сложении двух векторов со­гласно уравнению (3.26) получим вектор напряжения источника 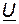(рис. 3.7, б).

 

 

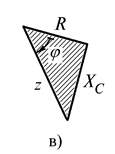
Рис. 24. Цепь, содержащая резистор и конденсатор

 

Из векторной диаграммы следует:

 

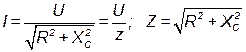, (41)

 

где 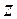– полное сопротивление цепи .

 

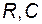Вектор напряжения источника отстает от вектора тока на угол 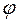, поэтому говорят, что цепь носит емкостный характер (– 9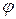0°< <0).

Для треугольника напряжений (рис. 24, б) и треугольника сопротивлений (рис. 24, в) можно записать соотношения, аналогичные соотношениям (34), (36) и (39)..

 

Последовательное соединение резистора, катушки и конденсатора

 

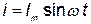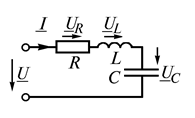
При протекании синусоидального тока по цепи, состоящей из последовательно соединенных элементов 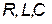(рис. 25, а), на ее зажимах создается синусоидальное напряжение, равное алгебраиче­ской сумме синусоидальных напряжений на отдельных элементах (второй за­кон Кирхгофа):

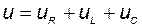. (42)

 

Для действующих значений это уравнение имеет вид

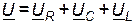. (43)

 

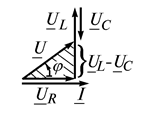
Построим векторную диаграмму с учетом известных фазовых соотношений (рис. 25, б). Вектор напряжения на резисторе совпадает по фазе с вектором тока, на конденсаторе он отстает от вектора тока на 90°, а на катушке опережает вектор тока на 90°. Сумма этих векторов напряжения на элементах цепи даст вектор напряжения источника.

 

а) б) в)

 

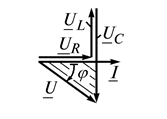
Рис. 25. Последовательное соединение резистора, катушки и конденсатора

 

Из векторной диаграммы определяем входное напряжение

 

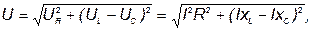
(44)

 

откуда ток и полное сопротивление:

 

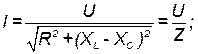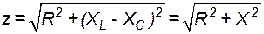, (45)

 

где 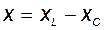– разность индуктивного и емкостного сопротивлений, называе­мая реактивным сопротивлением.

 

Сдвиг фаз определим из треугольника напряжений или сопротивлений:

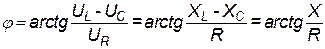.   (46)

Если 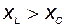, т. е. 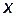> 0, то цепь имеет индуктивный характер. В этом слу­чае 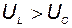(рис. 25 б), а сдвиг фаз 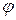> 0. Если 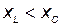, т.е. 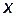< 0, то цепь имеет емкостный характер и сдвиг фаз 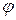< 0 (рис. 25, в). Таким образом, реактивное сопротивление 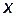может быть положительным ( 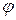> 0) и отрицательным ( 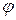< 0).

 

Экспериментальная часть

Схема испытаний показана на рис. 26.

 

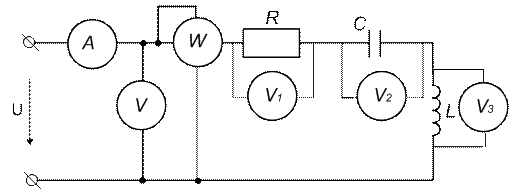
а)

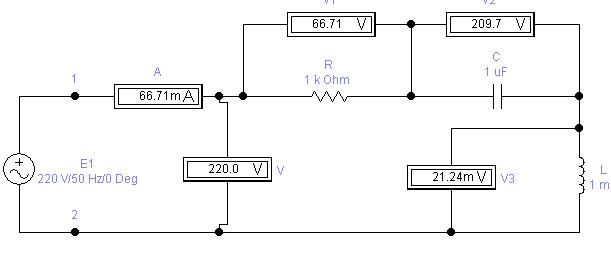
б)

 

а) – в обычном формате; в Elektronic WorkBench 5.12

 

Рис. 26. Экспериментальная схема

 

Напряжение на схему подается от лабораторного источника напряжения однофазного переменного тока. Реостат, батарея конденсаторов, индуктивные катушки собираются в схему на стенде при помощи наборной панели. В качестве амперметра, вольтметра используются мультиметры, установленные на стенде. Ваттметр используется настольный.

 

Порядок выполнения работы

 

1. Ознакомиться с виртуальными приборами и другим оборудованием, используемыми в работе.

2. Собрать исследуемую схему в оболочке EWB, но без батареи конденсаторов. Проделать опыт с каждой из 2-х катушек индуктивности. Показания приборов занести в табл. 6.

3. Собрать схему без катушки индуктивности, но включающую батарею конденсаторов. Попеременно включая в цепь конденсаторы, снять показания приборов и их данные занести в табл. 6.

4. Собрать схему, указанную на рис. 26. Данные приборов занести в табл. 6.

5. Вычислить активные, реактивные и комплекс полного сопротивления, индуктивность катушки и угол сдвига фаз в цепи с катушкой индуктивности. Полученные результаты свести в табл. 6.

6. Вычислить активные, реактивные и комплекс полного сопротивления, емкость конденсатора и угол сдвига фаз в цепи с конденсатором емкости. Полученные результаты свести в табл. 7.

7. Вычислить активные, реактивные и комплекс полного сопротивления, емкость конденсатора, индуктивность катушки и угол сдвига фаз в цепи с последовательным соединением резистора, катушки индуктивности и конденсатора емкости. Вычислить активную, реактивную и полную мощность цепи R, L, C. Определить характер цепи. Полученные результаты свести в табл. 8.