Резистор в цепи синусоидального тока

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Если синусоидальное напряжение 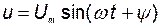(рис. 20, а) подклю­чить к резистору с сопротивлением 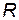, то через него будет протекать синусоидаль­ный ток

 

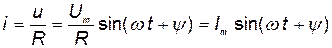. (16)

 

Следовательно, напряжение на зажимах и ток, проходящий через резистор, имеют одинаковую начальную фазу, или совпадают по фазе, – они одновременно достигают своих амплитудных значений и соответственно одно­временно проходят через нуль (рис. 20, б, в).

Разность начальных фаз двух синусоид называют углом сдвига фаз. В дан­ном случае угол сдвига фаз между напряжением и током равен нулю:

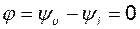. (16)

 

Амплитуды и действующие значения тока и напряжения связаны

 

 

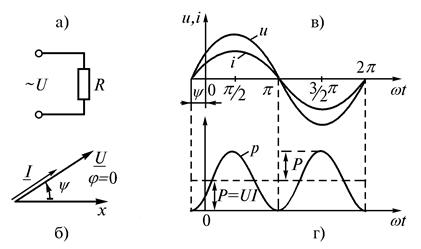
Рис. 20. Резистор в цепи синусоидального тока

 

 

законом Ома:

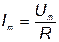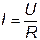; . (17)

 

Протекание тока через резистор сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Мгно­венная мощность, потребляемая резистором:

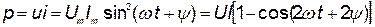  , (18)

 

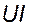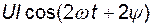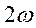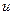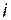изменяется с угловой частотой, удвоенной по сравнению с частотой напряжения и тока. Мгновенная мощность имеет постоянную составляющую и составляю­щую , изменяющуюся с частотой (рис. 20, г). Так как и совпадают по фазе, т. е. всегда имеют одинаковый знак, то их произведение всегда положительно, следовательно, 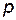> 0. Среднее значение мгновенной мощности за период:

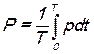
(19)

 

называется активной мощностью и измеряется в ваттах.

В данном случае актив­ная мощность

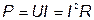. (20)

 

Отсюда активное сопротивление

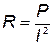. (21)

 

Известно, что сопротивление проводника переменному току больше, чем постоянному вследствие явления поверхностного эффекта.

 

Индуктивная катушка в цепи синусоидального тока

Индуктивная катушка как элемент схемы замещения реальной цепи синусои­дального тока дает возможность учитывать при расчете явление самоиндук­ции и явление накопления энергии в ее магнитном поле. Пусть в цепь перемен­ного тока (рис. 21, а) включена катушка с бесконечно малым сопро­тивлением провода 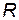= 0. Непрерывное во времени изменение тока вызывает появ­ление в витках катушки ЭДС самоиндукции. В соответствии с правилом Ленца эта ЭДС противодействует изменению тока.

Допустим, ток через катушку изменяется по закону:

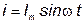. (22)

 

В этом случае ЭДС самоиндукции:

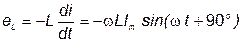. (23)

 

Поэтому напряжение на катушке:

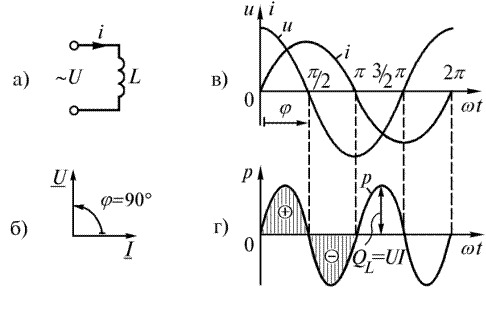
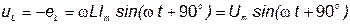. (24)
   
 


Сравнивая формулы (22) и (24), можно сделать вывод о том, что напряже­ние на катушке опережает ток на угол 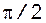или ток отстает от напряжения по фазе на угол 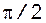(рис 21, б). Угол сдвига фаз в этом случае положительный (рис. 3.4, в) .

 

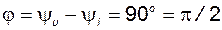Рис. 21. Катушка в цепи синусоидального тока

 

Параметр цепи 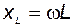– индуктивное сопротивление, имеющее размерность Ом. Оно зависит от частоты и представляет собой величину, с помо­щью которой учитывается явление самоиндукции. Из анализа (22) видно, что амплитуды напряжения и тока связаны законом Ома:

.

 

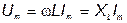Аналогично для действующих значений

.

 

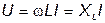Мгновенная мощность цепи с катушкой:

 

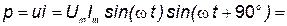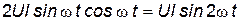. (25)

 

Из графика (рис. 21, г), построенного по уравнению (25), видно, что за пер­вую четверть периода, когда 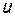> 0 и 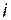> 0, площадь, ограниченная кривой 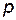и осью абсцисс, пропорциональна энергии, потребляемой катушкой на создание магнитного поля. Во вторую четверть периода (ток убывает от максимума до нуля) энергия магнитного поля катушки передается источнику питания. При этом мгновен­ная мощность отрицательна, а процесс повторяется. Таким образом, происходит колебание энергии между источником и катушкой, причем активная мощность, поступающая в катушку, равна нулю. Амплитуду колебания мгновенной мощ­ности в цепи с катушкой называют реактивной (индуктивной) мощностью, определяемой выражением

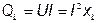. (26)

 

Реактивную мощность в отличие от активной мощности измеряют в вар (вольт-ампер реактивный).