Кроме частотных характеристик используются логарифмические частотные характеристики – логарифмическая амплитудно-частотная (ЛАЧХ) и логарифмическая фазовая частотная (ЛФЧХ) характеристики.
ЛАЧХ – это зависимость 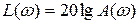 от логарифма частоты
от логарифма частоты 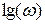 . При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат
. При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат 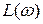 .
.
ЛФЧХ – это зависимость фазовой частотной функции 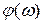 от логарифма частоты
от логарифма частоты 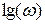 . При ее построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают
. При ее построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают 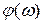 в градусах или радианах.
в градусах или радианах.
За единицу масштаба по оси абсцисс принимается декада – частотный интервал, соответствующий изменению частоты в 10 раз. Ось ординат при построении этих характеристик проводят через произвольную, удобную для рассматриваемой задачи, точку, а не через точку w=0, поскольку частоте w=0 соответствует бесконечно удаленная точка.
Единицей 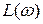 является децибел (дБ), равный одной десятой Бела. Бел – это единица десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 Бел соответствует усилению мощности в 10 раз. Поскольку мощность сигнала пропорциональна квадрату амплитуды, а
является децибел (дБ), равный одной десятой Бела. Бел – это единица десятичного логарифма коэффициента усиления мощности сигнала, т.е. 1 Бел соответствует усилению мощности в 10 раз. Поскольку мощность сигнала пропорциональна квадрату амплитуды, а 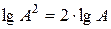 , то усиление в Белах, выраженное через отношение амплитуд, равно
, то усиление в Белах, выраженное через отношение амплитуд, равно 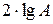 .
. 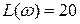 дБ означает, что на данной частоте при прохождении сигнала через цепь его амплитуда увеличивается в 10 раз.
дБ означает, что на данной частоте при прохождении сигнала через цепь его амплитуда увеличивается в 10 раз.
ЛАЧХ и ЛФЧХ за счет использования логарифмических шкал более удобны при анализе работы цепи в широком диапазоне изменения частоты сигнала.
Измеритель диаграмм Боде предназначен для измерения АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ электрических цепей.
5.1 Собрать схему, приведенную на рис. 10. Установить параметры элементов схемы в соответствии с вариантом (см. табл. 2).
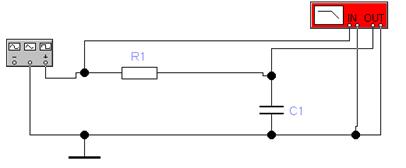
Рис. 10 Схема измерения частотных характеристик цепи
На выходе генератора установить гармонические колебания с заданной амплитудой и частотой.
5.2 На экране измерителя диаграмм Боде получить устойчивое изображение ЛАЧХ или АЧХ цепи (рис. 11). С помощью визирной линии снять несколько значений ЛАЧХ (или АЧХ) и зарисовать ее в отчете. Сделать выводы.
5.3 RC-цепь, представленная на рис. 10, представляет собой пассивный фильтр низких частот. Конденсатор С1 для сигнала низкой частоты (ниже частоты среза) является большим сопротивлением и сигнал поступает на выход фильтра. Для сигнала высокой частоты (выше частоты среза) конденсатор является хорошим проводником и поэтому он шунтирует данный сигнал, не пропуская его на выход. Частотой среза 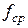 называется частота, при которой напряжение на выходе фильтра падает до уровня 0,707 от напряжения в полосе пропускания (т.е. падает на 3 дБ). Для случая, представленного на рис. 11 частота среза фильтра составляет приблизительно
называется частота, при которой напряжение на выходе фильтра падает до уровня 0,707 от напряжения в полосе пропускания (т.е. падает на 3 дБ). Для случая, представленного на рис. 11 частота среза фильтра составляет приблизительно 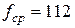 Гц, т.е. выше данной частоты амплитуда сигнала на выходе фильтра как видно из ЛАЧХ все более ослабевает.
Гц, т.е. выше данной частоты амплитуда сигнала на выходе фильтра как видно из ЛАЧХ все более ослабевает.
5.4 Определить частоту среза фильтра.

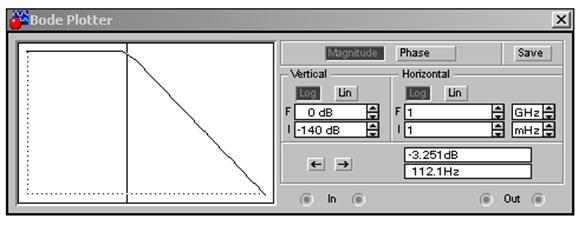
Рис. 11 ЛАЧХ цепи и значение частоты среза фильтра
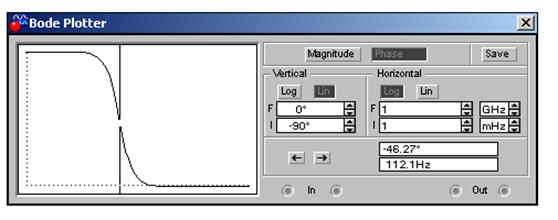
Рис. 12 ЛФЧХ цепи
5.5 Нажатием кнопки Phase на панели управления измерителя, а также кнопками настройки прибора получить устойчивое изображение ЛФЧХ или ФЧХ цепи (рис. 12). С помощью визирной линии снять несколько значений ЛФЧХ (или ФЧХ) и зарисовать ее в отчете. Сделать выводы.
2. Лабораторная работа № 2. Исследование линейной
электрической цепи постоянного тока
Цель работы: экспериментальная проверка законов Ома, Кирхгофа и метода контурных токов.
Теоретическое обоснование
Законы Ома и Кирхгофа. Закон Ома устанавливает связь между током пассивной ветви и напряжением на ней, определяемый по формуле (10,11):
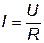 , ,
| (10) |
где R – полное сопротивление ветви, определяемое как сумма сопротивлений всех резисторов, входящих в данную ветвь.
Закон Ома позволяет определить также ток в активной ветви «аb», приведенной на рис. 13, если известны значения потенциалов точек а и b.

Рис. 13. Участок электрической цепи
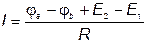 . .
| (11) |
Если положительные направления ЭДС и тока совпадают, то ЭДС записывается с положительным знаком, в противном случае – с отрицательным. Режим электрической цепи любой конфигурации описывается первым и вторым законами Кирхгофа.
Первый закон Кирхгофа выражается так: алгебраическая сумма токов в любом узле электрической цепи равна нулю (рис.12):
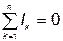 . .
| (12) |
Второй закон Кирхгофа: алгебраическая сумма падений напряжений по замкнутому контуру равна алгебраической сумме ЭДС (рис.13):
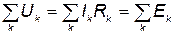 . .
| (13) |
Потенциальная диаграмма. Потенциальная диаграмма дает наглядное представление о распределении потенциала вдоль некоторого контура электрической цепи. На диаграмме по оси абсцисс откладывается значение сопротивлений участков в той последовательности, в которой они расположены в контуре, по оси ординат – потенциалы соответствующих точек. Потенциалы точек определяются относительно произвольной точки схемы, потенциал которой принимается равным нулю. При построении необходимо учитывать внутреннее сопротивление источников ЭДС.
Экспериментальная часть
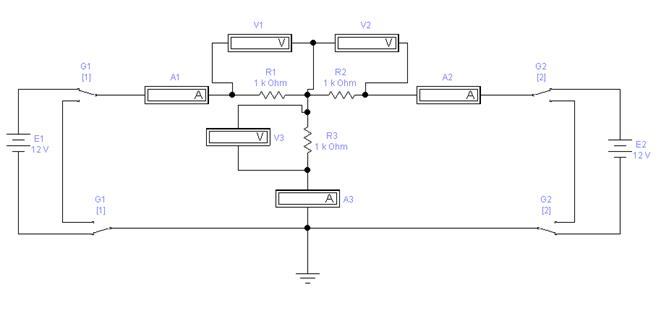
В работе исследуется линейная электрическая цепь постоянного тока с двумя источниками энергии в соответствии с рис. 14.
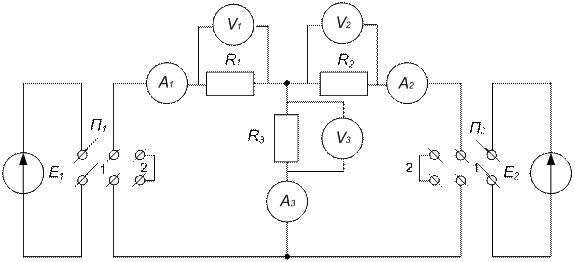
а)
б)
а) – схема в обычном формате; б) – в Elektronic WorkBench 5.12
Рис. 14. Экспериментальная схема
Напряжение источников питания подведены к переключателям П1 и П2, установленным на лабораторном стенде. Резисторы R1 , R2 , R3, амперметры А1 , А2 и А3 и вольтметр установлены также на стенде. Для измерения напряжений на всех участках цепи используется один вольтметр со щупами. Переключатели П1 и П2 устанавливаются в положение 1.
Порядок выполнения работы
1. Ознакомиться с виртуальными приборами и другим оборудованием, используемым в работе.
2. Собрать исследуемую схему в оболочке EWB.
3. Измерить ЭДС источников питания.
4. Поставив переключатели в положение 1, измерить и записать в табл. 3 все токи и напряжения на источниках и всех резисторах.
5. Поставив переключатель П2 в положение 2, вновь измерить все токи и напряжения при действии только одной ЭДС Е1.
6. Поставив переключатель П1 в положение 2, вновь измерить все токи и напряжения при действии только одной ЭДС Е3.
7. Убедиться, составив соответствующие уравнения, что в цепях соблюдаются законы Кирхгофа.
8. По данным измерений рассчитать величины сопротивления резисторов R1 , R2 , R3 и внутреннее сопротивление источников r01 и r03 (рис.14):
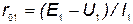 , , 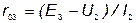 . .
| (14) |
9. При действии обоих ЭДС рассчитать токи в ветвях с помощью метода контурных токов, приняв за исходные измеренные ЭДС и рассчитанные сопротивления. Сравнить данные опыта и расчета.
10. Сформулировать выводы по работе, полученные результаты занести в табл. 3.
Таблица 3 - Результаты лабораторной работы № 2
| Положение переключа- телей | Измерено | Вычислено | ||||||||||||
| напряжение, В | токи, мА | сопротивление, Ом | ||||||||||||
| U1 | U2 | Ur1 | Ur2 | Ur3 | I1 | I2 | I3 | r1 | r2 | r3 | r4 | r01 | r03 | |
| П1 - 1 П2 - 1 | ||||||||||||||
| П1 - 1 П2 - 2 | ||||||||||||||
| П1 - 2 П2 - 1 | ||||||||||||||








