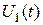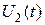3.4 По экспериментальным данным рассчитать коэффициент передачи .
3.5 Анализ RC-цепи показывает, что ее коэффициент передачи определяется выражением:
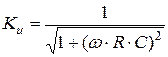, (8)
где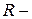 
сопротивление резистора R1 RC-цепи, (Ом);
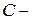значение емкости конденсатора C1 RC-цепи, (Ф);
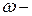циклическая частота гармонического сигнала, 
,
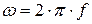(Гц).
Рассчитать по приведенной формуле коэффициент передачи и сравнить его со значением, полученным экспериментально.
Задание 4. Измерение с помощью двухканального осциллографа фазового сдвига двух гармонических сигналов в простейших RC (RL) – цепях.
4.1 Собрать схему, приведенную на рис. 5. Установить параметры элементов схемы в соответствии с вариантом (см. табл. 2).
4.2 На выходе генератора установить гармонические колебания с заданной амплитудой и частотой.
4.3 На экране осциллографа получить устойчивое не искаженное изображение обоих сигналов и определить их фазовый сдвиг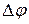 
. Фазовый сдвиг 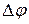можно определить с помощью следующей формулы:
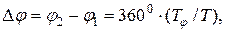(9)
где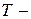 
период сигнала (рис. 6);
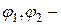начальные фазы входного и выходного сигналов;
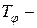временной сдвиг между сигналами (рис. 7).
|
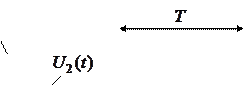
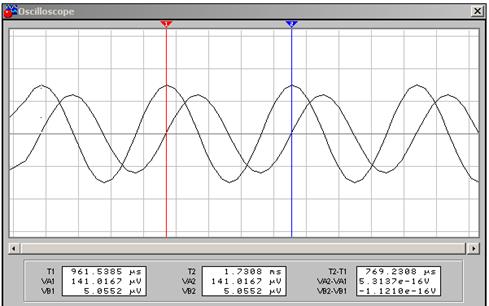
Рис. 6 Измерение периода сигнала
Временной сдвиг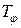 
на экране осциллографа можно измерить, используя визирные линии, которые ориентируют по максимуму гармонической функции, как показано на рис. 7. Величину временного сдвига можно прочесть в окне под экраном (см. рис. 7).
Для случая, приведенного на рис. 6-7 величина фазового сдвига двух гармонических сигналов составит
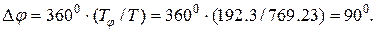
Результаты измерений и расчетов занести в отчет.
|
|
|
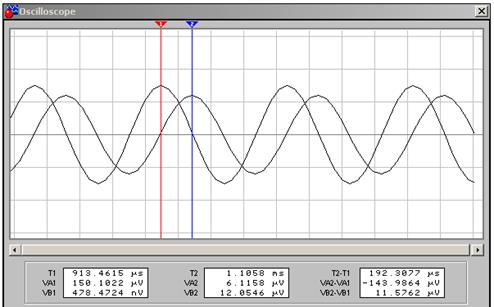
Рис. 7 Измерение временного сдвига двух гармонических сигналов
Следует отметить, что выходной сигнал может отставать по фазе от входного сигнала и тогда он располагается справа от входного (рис. 7). Фазовый сдвиг в этом случае берется со знаком минус. В случае опережения выходного сигнала (он располагается слева от входного) фазовый сдвиг берется положительным. На рис. 7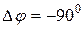 
. Выходной сигнал отстает по фазе от входного на 
.
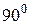Задание 5. Измерение частотных характеристик простейших RC (RL) – цепей с помощью измерителя диаграмм Боде
Частотными характеристиками цепи называют функции, характеризующие реакцию цепи на синусоидальное входное воздействие в установившемся режиме. Данные характеристики имеют очень большое значение при анализе работы цепи. Кратко охарактеризуем каждую из характеристик. Если на вход цепи подается величина (рис. 8)
 |
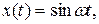
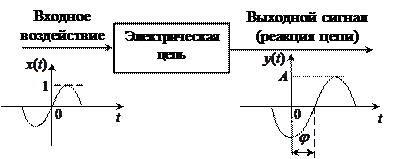Рис. 8 К определению частотной характеристики цепи
то на выходе в установившемся режиме получаем:
,
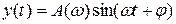где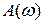 
– амплитуда, 
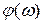– фаза сигнала, 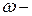циклическая частота.
Каждой гармонической функции времени можно поставить в соответствие комплексное число, называемое мгновенным комплексом гармонической функции (рис. 9)
.
 |
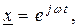
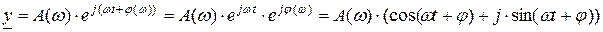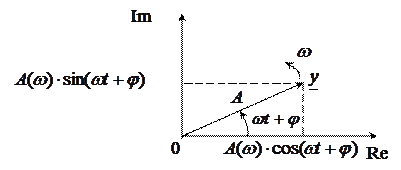Рис. 9 Векторная диаграмма
Функцию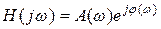 
называют амплитудно-фазовой частотной характеристикой цепи (АФЧХ). Функция 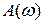называется соответственно амплитудно-частотной характеристикой цепи (АЧХ), 
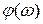– фазовой частотной характеристикой цепи (ФЧХ). Функцию 
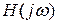можно представить в виде:
,
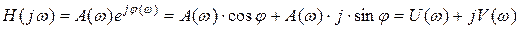где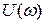 
и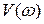 
– соответственно вещественная и мнимая частотные характеристики.
Исходя из этого, функции АЧХ и ФЧХ можно представить как:
,
.
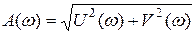
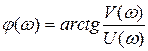