Так как у нас достаточно большая выборка, то для удобства построения гистограммы по формуле 1.1 посчитаем выборочный размах.
Введение.
Важнейшим источником роста эффективности производства является постоянное повышение технического уровня и качества выпускаемой продукции. Причем, проблема повышения качества продукции актуальна на каждом предприятии, но не каждое готово затрачивать свои материальные ресурсы на постоянную модернизацию технологий изготовления того или иного продукта. Все организации пытаются удерживать свою продукцию на постоянном максимально высоком уровне. В связи с этим был создан отдел управления и контроля качества выпускаемой продукции, который использует различные методы для поддержания качества. Такие как: диаграммы, гистограммы, контрольные карты и пр.
Качество продукции является одним из самых важных проблем на сегодняшний день. Современная рыночная экономика предъявляет принципиально новые требования к качеству выпускаемой продукции. Это связанно с тем, что сейчас выживаемость любой фирмы, ее устойчивое положение на рынке товаров и услуг определяется уровнем конкурентоспособности. В свою очередь, конкурентоспособность связана с действием нескольких десятков факторов, среди которых можно выделить два основных – уровень цены и качество продукции. Причем второй фактор постепенно выходит на первое место.
Управление качеством является одной из ключевых функций как корпоративного, так и проектного менеджмента, основным средством достижения и поддержания конкурентоспособности любого предприятия.
Ключевой задачей менеджмента компаний является создание, практическая реализация и последующая сертификация системы менеджмента качества.
По факту управление качеством является аспектом системы управления предприятия, подобно таким, как затраты, время и управление персоналом, именно это положение находится в основе принципов современной системы менеджмента качества.
Так как качество является неотъемлемым элементом любого процесса, а для его повышения необходимо: во-первых, прислушиваться к потребителю, во-вторых, внедрять новые технологии, в-третьих, обучать персонал, в-четвертых, контролировать весь процесс, а не только его результат и т.д., то эти принципы легли в основу популярного направления управления качеством – Total Quality Management.
Существуют различные методы контроля качества, среди которых наиболее важные – статистические методы качества. Эти методы позволяют при необходимости совершенствовать качество процесса приготовления и конечный результат продукта.
К основным методам инструмента контроля качества относятся:
гистограмма, диаграмма Парето, диаграмма разброса; причинно-следственная диаграмма, контрольная карта, контрольный листок.
Эти методы позволяют при необходимости совершенствовать качество процесса приготовления и конечный результат продукта.
Моим объектом исследования является Закрытое Акционерное Общество «Воронежский комбинат строительных материалов» (ЗАО «ВКСМ»), располагающийся на берегу реки «Дон» вблизи Воронежа. Комбинат обеспечен квалифицированным персоналом (около 1100 человек), имеет подъездные железнодорожные и автомобильные пути, устойчивое энергоснабжение.
Завод начал свою деятельность 14 января 1955 г. В том году было произведено 46 млн шт. силикатного кирпича, а запуск второй очереди в 1959 году позволил произвести 176 млн шт. кирпича, а в 1969 после расширения завода его мощность достигла 360 млн шт. кирпича в год.
В 1963 году был построен и запущен цех по производству полужестких минераловатных плит мощностью 100 тыс. м2.
В 2003 году после реконструкции одного из кирпичных цехов с переводом на производство ячеисто – бетонных блоков по импортной технологии, после чего мощность цеха достигла 120 тыс. м3 блоков в год.
В 2009 году была сдана в эксплуатацию линия, производящая песчано-цементные изделия (тротуарная плитка, бордюрный камень, блоки). А в 2011 году был переоснащен цех по производству газосиликатных блоков, мощностью до 800 м3.
Задание на курсовую работу:
1. Тема работы: применение статистических методов управления качеством.
2. Задание: изучить основные методы контроля качества на примере производства газосиликатных блоков.
· Определить основные причины брака, с помощью диаграмм Парето;
· Построить гистограмму
1. Диаграмма Парето.
Диаграмма, или как ее еще называют, кривая Парето является графическим изображением зависимости распределения определенных ресурсов или результатов от выборки, для выявления наиболее значимой причины несоответствия. Таким образом, при помощи этой диаграммы возможно устранить, или свести к минимуму, те причины, по которым производство выпускает максимальное количество дефектной продукции.
Для этого составим таблицу 1, в которой укажем выявленные дефекты при изготовления газосиликатных блоков.
Причины дефектов газосиликатного блока:
1. Материал низкого качества (м);
2. Неудовлетворительный фракционный состав песка (ф);
3. Слишком мягкий раствор для изготовления блоков (р);
4. Ошибки технологического характера (т);
5. Повышенная влажность (в).
Таблица 1. Факторы и причины, влияющие на возникновение дефектов газосиликатного блока.
| Мастер | Линия | Пн. | Вт. | Ср. | Чт. | Пт. |
| А | 1 | мммм фф рр тт в | ммммм ф рр тт | ммммм ффффф рр тт в | мммм ф рр тт | ммммм ф рррр ттт |
| 2 | мм ф р | ммм фф рр в | ммм ффффф рр т | мм ф р т | мм фф р т | |
| В | 1 | мммм ф р | мммм ф р | ммм ффффф р т | ммм ф р т в | мммм ф рр т |
| 2 | мм ф рр в | ммм ф р т | ммм фффф рр т | ммм ф т | мм ф рр т |
1.1 Построение общей диаграммы Парето
Для построения общей диаграммы Парето необходимо проранжировать данные значения в порядке убывания факторов, после чего рассчитать воздействие в процентах (таблица 1.1). Общая диаграмма Парето представлена на рисунке 1.1.
Таблица 1.1 Проранжированные значения факторов, влияющие на появление дефектов газосиликатного блока.
| Причина | Количество дефектных блоков | Воздействие, % | Суммарное воздействие, % |
| м | 66 | 40,5 | 40,5 |
| ф | 38 | 23,3 | 63,8 |
| р | 33 | 20,2 | 84 |
| т | 21 | 12,9 | 96,9 |
| в | 5 | 3,1 | 100 |
| Сумма | 163 | 100 |
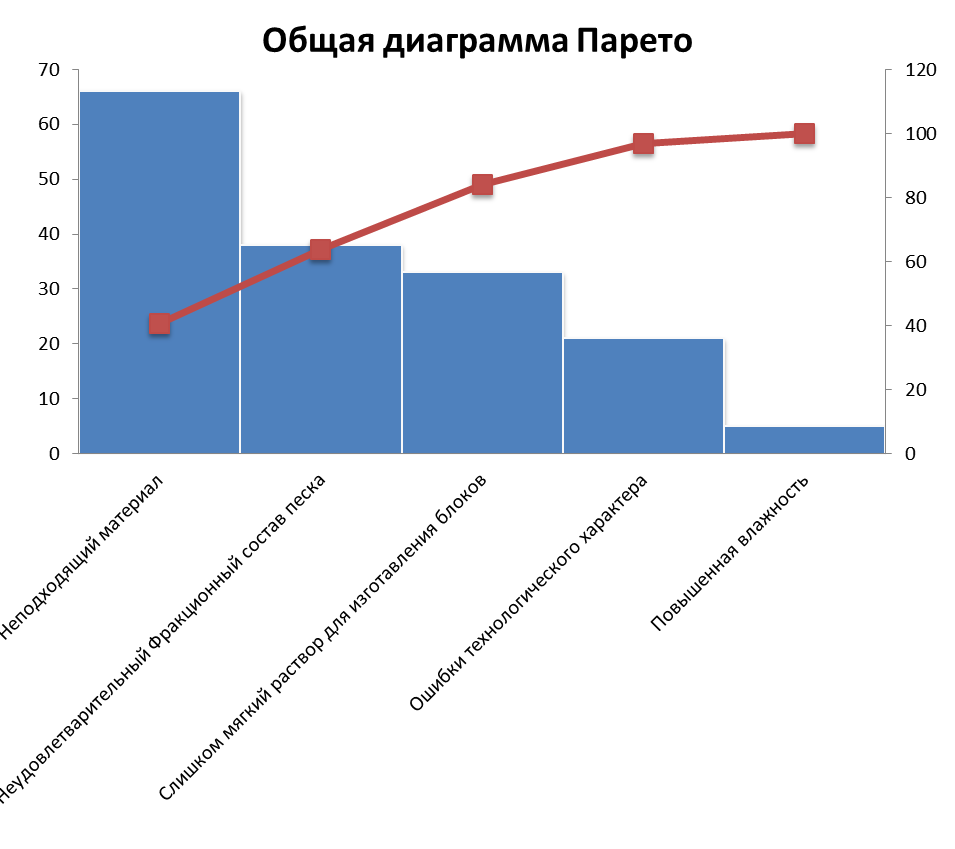 Рисунок 1.1 Общая диаграмма Парето
Рисунок 1.1 Общая диаграмма Парето
1.2 Построение диаграммы Парето для мастера А
Для построения диаграммы Парето необходимо проранжировать данные значения для мастера А в порядке убывания факторов, после чего рассчитать воздействие в процентах (таблица 1.2). Диаграмма Парето для мастера А представлена на рисунке 1.2.
Таблица 1.2 Проранжированные значения факторов, влияющие на появление дефектов газосиликатного блока.
| Причина | Количество дефектных блоков | Воздействие, % | Суммарное воздействие, % |
| м | 35 | 37,6 | 37,6 |
| ф | 21 | 22,6 | 60,2 |
| р | 20 | 21,5 | 81,7 |
| т | 14 | 15,1 | 96,8 |
| в | 3 | 3,2 | 100 |
| Сумма | 93 | 100 |
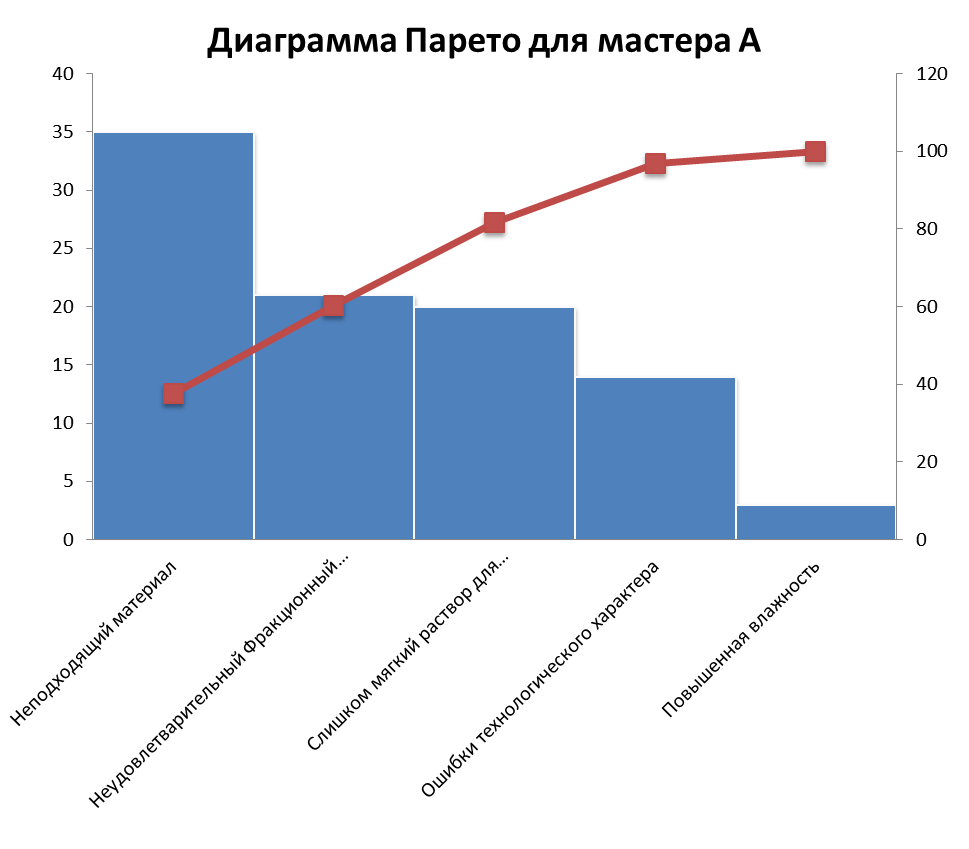 Рисунок 1.2 диаграмма Парето для мастера А
Рисунок 1.2 диаграмма Парето для мастера А
1.3 Построение диаграммы Парето для мастера В
Для построения диаграммы Парето необходимо проранжировать данные значения для мастера В в порядке убывания факторов, после чего рассчитать воздействие в процентах (таблица 1.3). Диаграмма Парето для мастера В представлена на рисунке 1.3.
Таблица 1.3 Проранжированные значения факторов, влияющие на появление дефектов газосиликатного блока.
| Причина | Количество дефектных блоков | Воздействие, % | Суммарное воздействие, % |
| м | 31 | 44,3 | 44,3 |
| ф | 17 | 24,3 | 68,6 |
| р | 13 | 18,6 | 87,2 |
| т | 7 | 10 | 97,2 |
| в | 2 | 2,8 | 100 |
| Сумма | 70 | 100 |
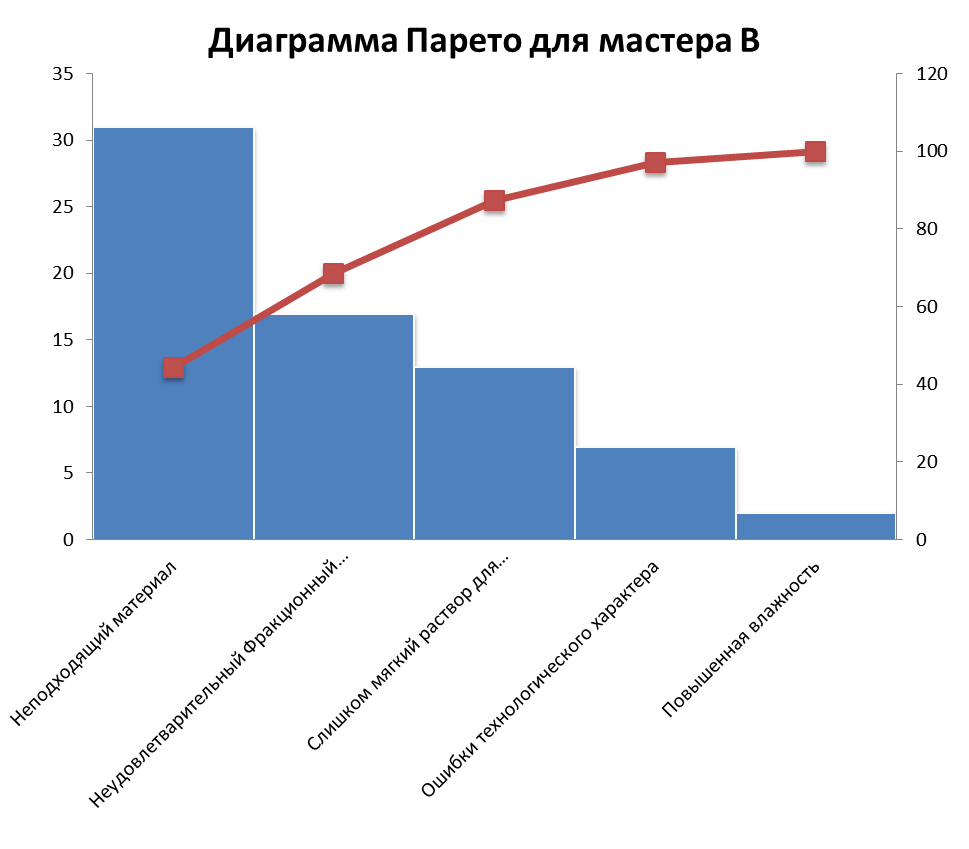 Рисунок 1.3 диаграмма Парето для мастера B
Рисунок 1.3 диаграмма Парето для мастера B
1.4 Построение диаграммы Парето для линии 1
Для построения диаграммы Парето необходимо проранжировать данные значения для линии 1 в порядке убывания факторов, после чего рассчитать воздействие в процентах (таблица 1.4). Диаграмма Парето для линии 1 представлена на рисунке 1.4.
Таблица1.4 Проранжированные значения факторов, влияющие на появление дефектов газосиликатного блока.
| Причина | Количество дефектных блоков | Воздействие, % | Суммарное воздействие, % |
| м | 41 | 42,7 | 42,7 |
| ф | 19 | 19,8 | 62,5 |
| р | 19 | 19,8 | 82,3 |
| т | 14 | 14,6 | 96,9 |
| в | 3 | 3,1 | 100 |
| Сумма | 96 | 100 |
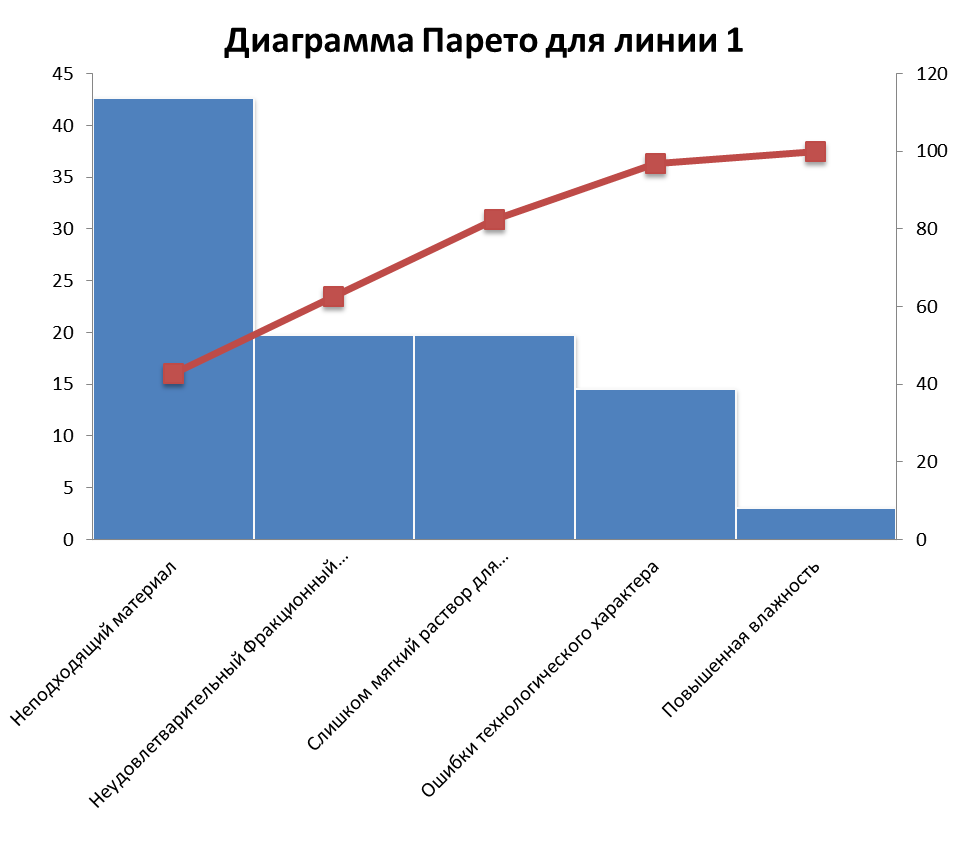 Рисунок 1.4 диаграмма Парето для линии 1
Рисунок 1.4 диаграмма Парето для линии 1
1.5 Построение диаграммы Парето для линии 2
Для построения диаграммы Парето необходимо проранжировать данные значения для линии 2 в порядке убывания факторов, после чего рассчитать воздействие в процентах (таблица 1.5). Диаграмма Парето для линии 2 представлена на рисунке 1.5.
Таблица 1.5 Проранжированные значения факторов, влияющие на появление дефектов газосиликатного блока.
| Причина | Количество дефектных блоков | Воздействие, % | Суммарное воздействие, % |
| м | 25 | 37,3 | 37,3 |
| ф | 19 | 28,4 | 65,7 |
| р | 14 | 20,9 | 86,6 |
| т | 7 | 10,4 | 97 |
| в | 2 | 3 | 100 |
| Сумма | 67 | 100 |
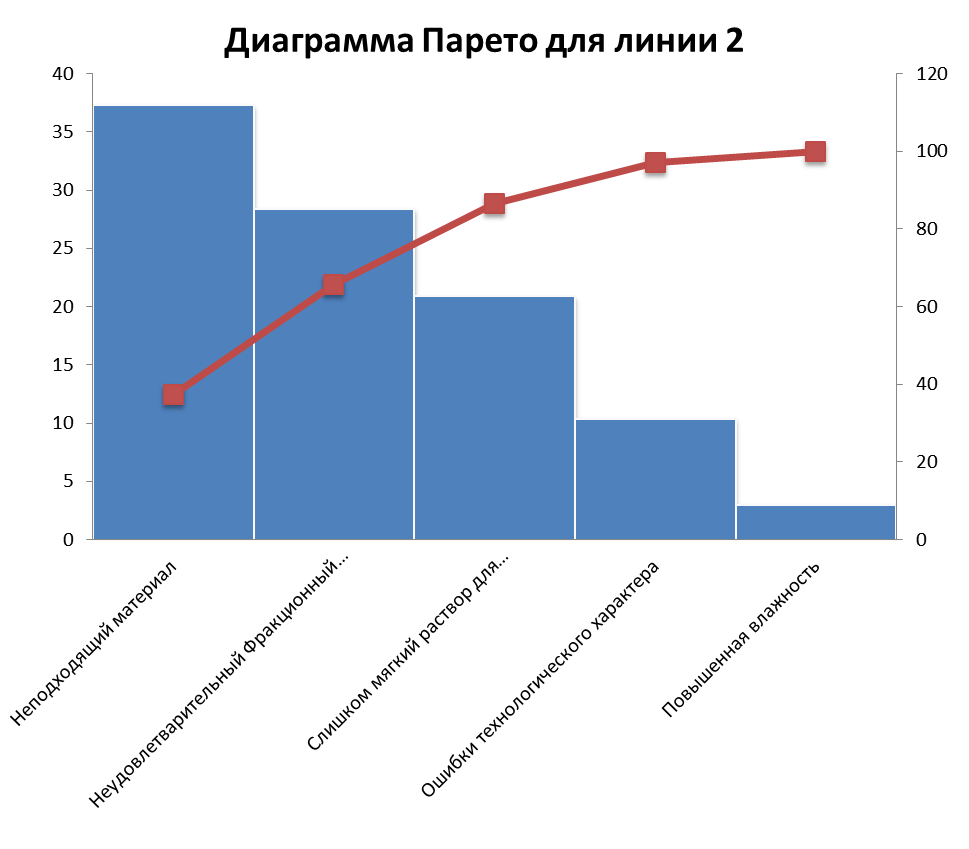 Рисунок 1.5 диаграмма Парето для линии 2
Рисунок 1.5 диаграмма Парето для линии 2
1.6 Выводы
Из диаграммы Парето, представленной на рисунке 2.1 видно, что основной причиной появления дефектов при производстве газосиликатных блоков является неподходящий материал. Из рисунков 2.2 и 2.3 видно что при работе мастера Б возникает меньше дефектов. Из рисунков 2.3 и 2.4 видно, что на линии 2 возникает меньше дефектов, но при этом она более чувствительна к фракционном составу песка.
2. Гистограмма.
На заводе по производству газосиликатных блоков работают две линии, которые посменно обслуживают два мастера (А и В). Для производства используют бетон D500, плотность блоков 480-510 кг/м3. Рассмотрим n газосиликатных блоков, с различной плотностью. В течение 10 дней за каждую смену на заводе по случайному закону отбирали 3 блока и производили расчет плотности. В результате данной процедуры получаем выборку, представленную в таблице 2.
Таблица 2. Результаты измерений плотности газосиликатных блоков.
| День | Мастер | Линия 1 | Линия 2 | ||||
| 1 | А | 512,3 | 505,5 | 508,6 | 484,6 | 484,2 | 508,0 |
| 2 | В | 480,2 | 480,0 | 498,0 | 491,1 | 505,2 | 494,8 |
| 3 | А | 507,8 | 498,2 | 494,4 | 507,4 | 486,6 | 494,7 |
| 4 | В | 484,2 | 504,9 | 503,1 | 502,3 | 483,3 | 501,6 |
| 5 | А | 507,6 | 481,1 | 509,3 | 505,9 | 512,1 | 491,2 |
| 6 | В | 493,4 | 495,0 | 483,9 | 477,4 | 508,6 | 501,3 |
| 7 | А | 493,9 | 507,2 | 488,4 | 501,8 | 497,9 | 484,6 |
| 8 | В | 486,5 | 482,3 | 488,9 | 494,6 | 485,4 | 502,6 |
| 9 | А | 491,6 | 486,6 | 483,6 | 481,8 | 505,6 | 489,1 |
| 10 | В | 487,3 | 488,7 | 500,9 | 482,5 | 489,0 | 497,1 |
2.1 Построим общую диаграмму процесса производства.
Если выборка содержит все возможные результаты измерений, то эти результаты представляют собой генеральную совокупность. Стоит заметить, что такая совокупность измерений может содержать как бесконечное множество элементов, так и конечное число. Чаще всего подобная выборка содержит лишь малую часть генеральной совокупности, поэтому и характеризует приближенное свойство данной совокупности. Так как полной статистической характеристикой является ее распределение, то для описания выборки используется гистограмма.
Так как у нас достаточно большая выборка, то для удобства построения гистограммы по формуле 1.1 посчитаем выборочный размах.
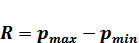 (1.1)
(1.1)
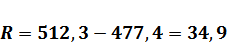 (1.2)
(1.2)
Определим по формуле 1.3 размер классов A, так чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины, длину которых h выберем равной 3.
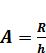 (1.3)
(1.3)
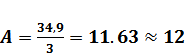 (1.4)
(1.4)
Определим нижнюю и верхнюю границы классов, так чтобы они включали наименьшее и наибольшее значения и середину классов, запишем значения в таблицу 2.1. Подсчитаем частоту f – блоков данного класса.
Далее обозначим нулем (u=0) тот класс, которому соответствует максимальная частота f, значение -1, для класса, следующего к наименьшему наблюдаемому значению, 1, 2, …10 для классов, следующих к наибольшему значению.
Рассчитаем вспомогательные значения 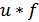 ,
, 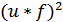 и
и 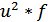 .
.
Таблица 2.1. Расчетная таблица для общей гистограммы.
| № п/п | Класс | Середина класса, х | Частота, f | u | uf | (uf)2 | u2f | |
| 1 | 477,0 | 480,0 | 478,5 | 1 | -2 | -2 | 4 | 4 |
| 2 | 480,0 | 483,0 | 481,5 | 6 | -1 | -6 | 36 | 6 |
| 3 | 483,0 | 486,0 | 484,5 | 8 | 0 | 0 | 0 | 0 |
| 4 | 486,0 | 489,0 | 487,5 | 7 | 1 | 7 | 49 | 7 |
| 5 | 489,0 | 492,0 | 490,5 | 5 | 2 | 10 | 100 | 20 |
| 6 | 492,0 | 495,0 | 493,5 | 6 | 3 | 18 | 324 | 54 |
| 7 | 495,0 | 498,0 | 496,5 | 3 | 4 | 12 | 144 | 48 |
| 8 | 498,0 | 501,0 | 499,5 | 3 | 5 | 15 | 225 | 75 |
| 9 | 501,0 | 504,0 | 502,5 | 6 | 6 | 36 | 1296 | 216 |
| 10 | 504,0 | 507,0 | 505,5 | 5 | 7 | 35 | 1225 | 245 |
| 11 | 507,0 | 510,0 | 508,5 | 8 | 8 | 64 | 4096 | 512 |
| 12 | 510,0 | 513,0 | 511,5 | 2 | 9 | 18 | 324 | 162 |
| Итого | 60 | - | 207 | 7823 | 1349 | |||
По формуле 1.5 найдем среднее арифметическое, где а – середина нулевого класса.
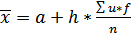 (1.5)
(1.5)
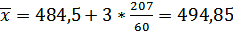 (1.6)
(1.6)
Определим по формуле 1.7 стандартное отклонение.
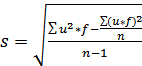 (1.7)
(1.7)
 (1.8)
(1.8)
Построим гистограмму с указанием объема выборки, среднего арифметического и стандартного отклонения (рисунок 2.1). Нанесем линию среднего арифметического.
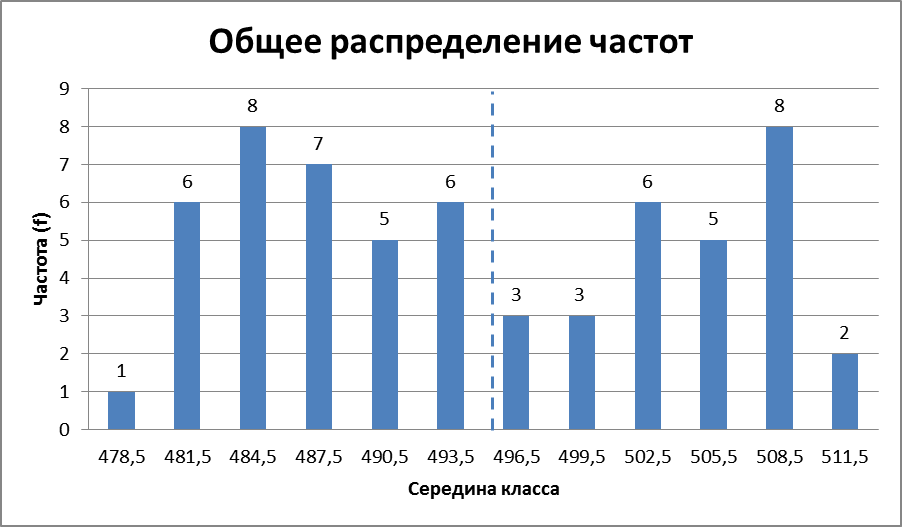
Рисунок 2.1. Гистограмма общего распределения частот для мастеров А и В – линии 1 и 2 (n=60, xср=494,85, s=4,54)
2.2Построим диаграмму процесса для линии 1.
Выборочный размах, длину интервала и размер классов оставим неизменными. Построим таблицу гистограммы линии 1 (таблица 2.2).
По формуле 5 найдем среднее арифметическое.
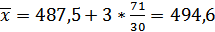 (1.9)
(1.9)
Определим по формуле 1.7 стандартное отклонение.
 (1.10)
(1.10)
Таблица 2.2 . Расчетная таблица гистограммы линии 1.
| № п/п | Класс | Середина класса, х | Частота, f | u | uf | (uf)2 | u2f | |
| 1 | 477,0 | 480,0 | 478,5 | 0 | -3 | 0 | 0 | 0 |
| 2 | 480,0 | 483,0 | 481,5 | 4 | -2 | -8 | 64 | 16 |
| 3 | 483,0 | 486,0 | 484,5 | 3 | -1 | -3 | 9 | 3 |
| 4 | 486,0 | 489,0 | 487,5 | 6 | 0 | 0 | 0 | 0 |
| 5 | 489,0 | 492,0 | 490,5 | 1 | 1 | 1 | 1 | 1 |
| 6 | 492,0 | 495,0 | 493,5 | 3 | 2 | 6 | 36 | 12 |
| 7 | 495,0 | 498,0 | 496,5 | 1 | 3 | 3 | 9 | 9 |
| 8 | 498,0 | 501,0 | 499,5 | 3 | 4 | 12 | 144 | 48 |
| 9 | 501,0 | 504,0 | 502,5 | 1 | 5 | 5 | 25 | 25 |
| 10 | 504,0 | 507,0 | 505,5 | 2 | 6 | 12 | 144 | 72 |
| 11 | 507,0 | 510,0 | 508,5 | 5 | 7 | 35 | 1225 | 245 |
| 12 | 510,0 | 513,0 | 511,5 | 1 | 8 | 8 | 64 | 64 |
| Итого | 30 | - | 71 | 1721 | 495 | |||
Построим гистограмму линии 1 с указанием объема выборки, среднего арифметического и стандартного отклонения (рисунок 2.2). Нанесем линию среднего арифметического.
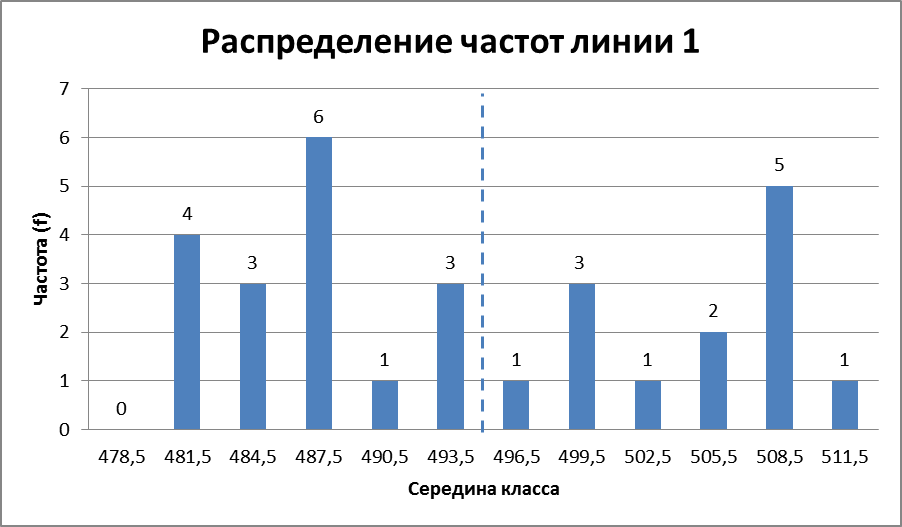
Рисунок 2. 2. Гистограмма общего распределения частот для мастеров А и В – линии 1 (n=30, xср=494,6, s=3,88)
2.3 Построим диаграмму процесса для линии 2.
Выборочный размах, длину интервала и размер классов оставим неизменными. Построим таблицу гистограммы линии 2 (таблица 2.3).
По формуле 1.5 найдем среднее арифметическое.
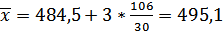 (1.11)
(1.11)
Определим по формуле 1.7 стандартное отклонение.
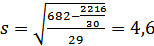 (1.12)
(1.12)
Таблица 2.3. Расчетная таблица гистограммы линии 2.
| № п/п | Класс | Середина класса, х | Частота, f | u | uf | (uf)2 | u2f | |
| 1 | 477,0 | 480,0 | 478,5 | 1 | -2 | -2 | 4 | 4 |
| 2 | 480,0 | 483,0 | 481,5 | 2 | -1 | -2 | 4 | 2 |
| 3 | 483,0 | 486,0 | 484,5 | 5 | 0 | 0 | 0 | 0 |
| 4 | 486,0 | 489,0 | 487,5 | 1 | 1 | 1 | 1 | 1 |
| 5 | 489,0 | 492,0 | 490,5 | 4 | 2 | 8 | 64 | 16 |
| 6 | 492,0 | 495,0 | 493,5 | 3 | 3 | 9 | 81 | 27 |
| 7 | 495,0 | 498,0 | 496,5 | 2 | 4 | 8 | 64 | 32 |
| 8 | 498,0 | 501,0 | 499,5 | 0 | 5 | 0 | 0 | 0 |
| 9 | 501,0 | 504,0 | 502,5 | 5 | 6 | 30 | 900 | 180 |
| 10 | 504,0 | 507,0 | 505,5 | 3 | 7 | 21 | 441 | 147 |
| 11 | 507,0 | 510,0 | 508,5 | 3 | 8 | 24 | 576 | 192 |
| 12 | 510,0 | 513,0 | 511,5 | 1 | 9 | 9 | 81 | 81 |
| Итого | 30 | - | 106 | 2216 | 682 | |||
Построим гистограмму линии 2 с указанием объема выборки, среднего арифметического и стандартного отклонения (рисунок 2.3). Нанесем линию среднего арифметического.
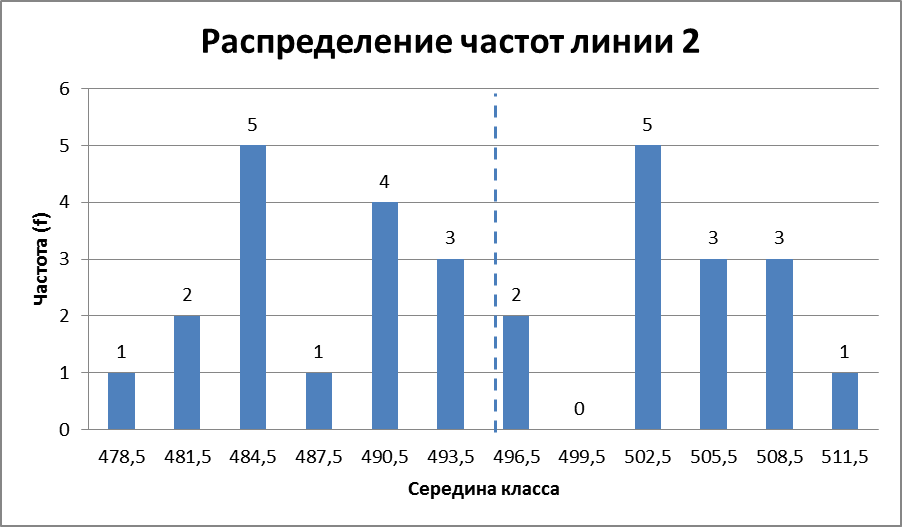
Рисунок 2.3. Гистограмма общего распределения частот для мастеров А и В – линии 2 (n=30, xср=495,1, s=4,6)
2.4 Построим диаграмму процесса для мастера А.








