ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 3. Принятие экономических решений в условиях неопределенности
Задача.
Выбрать оптимальный размер партии закупки в условиях неопределенности на основе критериев (табл. 3.1): 1) Лапласа
2) Вальда
3) Гурвица
4) Сэвиджа.
Уровень спроса не превышает 50 ед.
Таблица 3.1
Цены продукта на рынке
| № варианта | Цена оптовая, Цо, тыс.ден.ед. | Цена реализации, Цр, тыс.ден.ед. | Цена возврата, Цв, тыс.ден.ед. |
| 1 | 18 | 20 | 14 |
| 2 | 18 | 23 | 14 |
| 3 | 18 | 21 | 14 |
| 4 | 18 | 25 | 14 |
| 5 | 18 | 19 | 14 |
| 6 | 18 | 24 | 14 |
| 7 | 18 | 23 | 14 |
| 8 | 18 | 27 | 12 |
| 9 | 18 | 26 | 12 |
| 10 | 18 | 24 | 12 |
| 11 | 17 | 21 | 12 |
| 12 | 17 | 25 | 12 |
| 13 | 17 | 26 | 12 |
| 14 | 17 | 22 | 12 |
| 15 | 17 | 20 | 12 |
| 16 | 17 | 19 | 11 |
| 17 | 17 | 18 | 11 |
| 18 | 17 | 28 | 11 |
| 19 | 17 | 27 | 11 |
| 20 | 17 | 21 | 11 |
| 21 | 19 | 21 | 11 |
| 22 | 19 | 25 | 11 |
| 23 | 19 | 22 | 11 |
| 24 | 19 | 20 | 15 |
| 25 | 19 | 23 | 15 |
| 26 | 19 | 27 | 15 |
| 27 | 19 | 26 | 15 |
| 28 | 19 | 24 | 15 |
| 29 | 19 | 30 | 15 |
| 30 | 19 | 29 | 15 |
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
При принятии решений в условиях неопределенности используют критерии:
1) Лапласа;
2) Вальда;
3) Гурвица;
4) Сэвиджа.
Пример решения
Например, Цо = 5 ден.ед., Цр = 6 ден.ед., Цв = 3 ден.ед.
Предложение и спрос составляют по 40 шт. соответственно.
С учетом исходных данных: Пр = 6 – 5 = 1 .ден.ед.; Уб = 5 – 3 = 2 ден.ед.
1) Критерий Лапласа: все состояния считаются равновероятностными (вероятность совершения каждого события 6/30=0,2).
Составляется матрица выигрышей (табл. 3.2)
Таблица 3.2
Матрица выигрышей
|
| спрос | |||||
| 0 | 10 | 20 | 30 | 40 | ||
| предложение | 10 | - 20 | 10 | 10 | 10 | 10 |
| 20 | - 40 | - 10 | 20 | 20 | 20 | |
| 30 | - 60 | - 30 | 0 | 30 | 30 | |
| 40 | - 80 | - 50 | - 20 | 10 | 40 | |
Определяется сумма прибыли при различных вариантах предложений:
П(10)=(-20+10+10+10+10)*0,2=4 ден.ед.
П(20)=(-10-10+20+20+20)*0,2=2 ден.ед.
П(30)=(-60-30+30+30+30)*0,2= – 6 ден.ед.
П(40)=(-80-50-20+10+40)*0,2= – 20 ден.ед.
Выбирается максимальный уровень прибыли (4 ден.ед.), который получается при предложении 10 шт.
2) Критерий Вальда: выбирается максимальное значение из минимальных (из убытков определяется наименьший уровень).
Из матрицы выигрышей определяется наименьшие значения результатов:
П(10) = - 20 ден.ед.
П(20) = - 40 ден.ед.
П(30) = - 60 ден.ед.
П(40) = - 80 ден.ед.
По данному критерию будет выбрана 1-я стратегия по предложению 10 шт. при этом минимальные убытки составят 20ден.ед.
3) Критерий Гурвица: при выборе решений рекомендуется пользоваться средним результатом, характеризующим состояние между крайним пессимизмом и крайним оптимизмом.
Критериальное значение определяется по формуле:
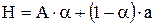, (3.1)
А – наилучший вариант (10);
a – наихудший вариант (-20);
α – коэффициент оптимизма (при α=0 – крайний пессимизм; при α=1 – крайний оптимизм).
Определяется вероятность, при которой события будут иметь среднее значение.
,
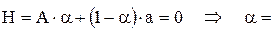| α | 0 | 1 | 0,5 | 0,7 | 0,6 | 0,65 |
| Н(10) | - 20 | 10 | - 5 | 1 | - 2 | 0 |
| Н(20) | - 40 | 20 | - 10 | 2 | - 4 | 0 |
| Н(30) | - 60 | 30 | - 15 | 3 | - 6 | 0 |
| H(40) | - 80 | 40 | - 20 | 4 | - 8 | 0 |
α=0,65.
4) Критерий Сэвиджа: минимизация уровня сожаления.
Необходимо учитывать не только возможные убытки, но и недополученную прибыль. В каждом столбце выбирается наилучшее значение, которое вычитается из всех элементов столбца – получают матрицу сожалений.
Таблица 3.3
Матрица сожалений
|
| спрос | |||||
| 0 | 10 | 20 | 30 | 40 | ||
| предложение | 0 | 0 | -10 | - 20 | - 30 | - 40 |
| 10 | - 20 | 0 | - 10 | - 20 | - 30 | |
| 20 | - 40 | - 20 | 0 | - 10 | - 20 | |
| 30 | - 60 | - 40 | - 20 | 0 | - 10 | |
| 40 | - 80 | - 60 | - 40 | - 20 | 0 | |
По каждому предложению из возможных уровней убытков выбирают максимальный:
П(0) = - 40 ден.ед.
П(10) = - 30 ден.ед.
П(20) = - 40 ден.ед.
П(30) = - 40 ден.ед.
П(40) = - 60 ден.ед.
Из возможных вариантов предложений рекомендуется ориентироваться на предложение 10 шт., позволяющий обеспечить минимизацию убытков до 30 ден.ед.