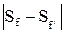ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 2. Проверка гипотез нормального распределения.
Используя исходные данные таблицы 1.1, проверить гипотезу нормального распределения заработной платы сотрудников предприятия по критериям согласия Пирсона Колмагорова, Ястремского и Романовского.
Сделать соответствующие выводы относительно характера распределения единиц в совокупности.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
Функция нормального распределения
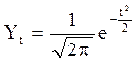, (2.1)
где
π = 3,1415
е = 2,7182
t – нормированное отклонение.
Нормированное отклонение
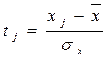. (2.2)
1) Критерий Пирсона
Основным показателем критерия Пирсона является расчетное значение кси-квадрат:
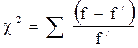(2.3)
Теоретические частоты рассчитываются по формуле:
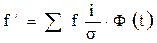(2.4)
где Ф(t) – значение функции нормального распределения (приложение А).
Фактическое значение кси-квадрат сравнивается с табличным (приложение Б), зависит от числа степеней свободы k (m – количество интервалов в вариационном ряду; r - число ограничений свободы).
( 
)
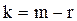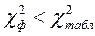(2.5)
При выполнении указанного выше условия, когда кси-квадрат фактическое меньше кси-квадрат табличного, гипотеза о нормальном распределении подтверждается.
2) Критерий Колмогорова
Основным показателем по критерию Колмагорова является значение λ, которое рассчитывается по формуле
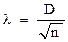, (2.6)
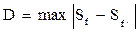, (2.7)
где n – сумма частот.
По рассчитанному значению λ в таблице определяется значение вероятности, с которой можно считать, что совокупность значений распределена в соответствии с законом нормального распределения (приложение В).
3) Критерий Романовского
Критерий Романовского уточняет критерий Пирсона следующим образом:
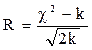(2.8)
Критерий Романовского:
R<3 – гипотеза о нормальном распределении подтверждается;
R>3 – гипотеза о нормальном распределении отвергается.
4) Критерий Ястремского
Критерий Ястремского (L) позволяет уточнять критерий Пирсона для вариационных рядов с числом интервалов более 20.
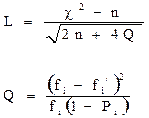(2.9)
при n<20 Q = 0,6
Критерий Ястремского:
L <3 – гипотеза о нормальном распределении подтверждается;
L >3 – гипотеза о нормальном распределении отвергается.
Пример решения.
1) Критерий Пирсона
Таблица 2.1
Распределение количества заказов по объемам дневного потребления материалов
| Объем дневного потребления материалов, тыс. ден.ед. | Кол-во заказов, шт. (f) |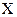 
| Хf |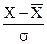 
| Ф(t) | f/ | (f-f/)2 |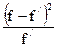 
|
| 40-42 42-44 44-46 46-48 48-50 50-52 52-54 | 4 7 28 35 16 6 4 | 41 43 45 47 49 51 53 | 164 301 1260 1645 784 306 212 | 2,22 1,44 0,67 0,11 0,88 1,66 2,43 | 0,0339 0,1415 0,3187 0,3965 0,2709 0,1006 0,0208 | 2 11 25 31 21 8 2 | 4 16 9 16 25 4 4 | 2,00 1,45 0,36 0,52 1,19 0,50 2,00 |
| Всего | 100 | - | 4672 | - | - | 100 | - | 8,02 |
Средний объем потребления материалов:
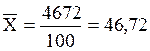тыс.ден.ед.
Среднеквадратическое отклонение от средних объемов потребления:
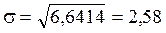
Для расчета теоретических частот рассчитывается следующее значение:
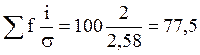
Теоретические частоты, заносимые в таблицу, в промежуточном варианте рассчитываются дробными величинами, а затем округляются до целого таким образом, чтобы общая сумма округленных значений теоретических частот была равной сумме фактических частот (Ʃf` = Ʃf).
Фактическое значение кси-квадрат это сумма значений в последней колонке расчетной таблицы:
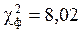
Табличное значение кси-квадрат определяется с вероятностью 0,99 при числе степеней свободы k=4):
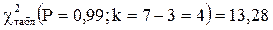
Сравнивается фактическое значение кси-квадрат с табличным значением кси-квадрат:
8,02 < 13,28
Таким образом, количество заказов по объемам дневного потребления материалов распределено в соответствии с законом нормального распределения, т.к.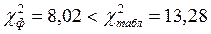 
2) Критерий Колмогорова
По приведенному выше примеру расчеты приводятся в виде следующей таблицы.
Таблица 2.2
Расчет параметров критерия Колмагорова
| Порядковый номер интервала | Кумулятивные частоты | Отклонение
| |
Фактические
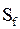
| Теоретические
| ||
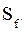
| 1 2 3 4 5 6 7 | 4 11 39 74 90 96 100 | 2 13 38 69 90 98 100 | 2 2 1 5 0 2 0 |
Критерий Колмагорова:
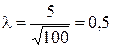
Таким образом, с вероятностью Р(t)=0,9639 можно считать, что совокупность объемов заказов распределена в соответствии с законом нормального распределения
3) Критерий Романовского
Расчет критерия R на основе приведенных выше значений:
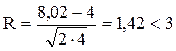
Совокупность заказов по объемам дневного потребления распределена по закону нормального распределения, т.к. R=1,42<3.
4) Критерий Ястремского
Расчет критерия L на основе приведенных выше значений:
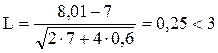
Совокупность заказов по объемам дневного потребления распределена по закону нормального распределения, т.к. L=0,25<3.