ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 1. Распределение единиц в совокупности.
Распределение работников предприятия по уровню заработной платы в подразделении приведено в таблице 1.1.
Определить показатели характера распределения единиц в совокупности:
- плотность распределения;
- асимметрию;
- эксцесс.
Таблица 1.1
Распределение работников предприятия по уровню заработной платы
| Зарплата, тыс. ден. ед. | Количество работников по вариантам, чел. | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 10-20 | 18 | 16 | 36 | 32 | 15 | 64 | 28 | 17 | 56 | 20 |
| 20-30 | 13 | 48 | 22 | 8 | 38 | 16 | 14 | 32 | 26 | 14 |
| 30-40 | 16 | 30 | 37 | 20 | 40 | 40 | 24 | 54 | 48 | 28 |
| 40-50 | 24 | 28 | 47 | 21 | 29 | 42 | 15 | 27 | 30 | 22 |
| 50-60 | 19 | 20 | 30 | 14 | 18 | 28 | 11 | 13 | 22 | 8 |
| 60-70 | 10 | 8 | 28 | 5 | 10 | 10 | 8 | 7 | 16 | 8 |
| 70-80 | 12 | 14 | 37 | 25 | 16 | 55 | 10 | 8 | 38 | 14 |
| Всего | ||||||||||
Продолжение таблицы 1.1
| Зарплата, тыс. ден. ед. | Количество работников по вариантам, чел. | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 10-20 | 38 | 40 | 41 | 28 | 44 | 45 | 21 | 48 | 50 | 51 |
| 20-30 | 20 | 20 | 19 | 12 | 29 | 19 | 17 | 17 | 16 | 23 |
| 30-40 | 44 | 46 | 47 | 32 | 52 | 51 | 36 | 55 | 54 | 61 |
| 40-50 | 25 | 24 | 24 | 12 | 46 | 22 | 12 | 18 | 20 | 19 |
| 50-60 | 13 | 13 | 12 | 9 | 10 | 8 | 9 | 8 | 7 | 27 |
| 60-70 | 9 | 8 | 7 | 7 | 19 | 5 | 5 | 4 | 4 | 18 |
| 70-80 | 22 | 24 | 37 | 25 | 36 | 41 | 10 | 38 | 38 | 51 |
| Всего | ||||||||||
Продолжение таблицы 1.1
| Зарплата, тыс. ден. ед | Количество работников по вариантам, чел. | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 10-20 | 53 | 54 | 56 | 24 | 31 | 37 | 53 | 63 | 64 | 66 |
| 20-30 | 36 | 15 | 14 | 14 | 13 | 13 | 26 | 28 | 11 | 11 |
| 30-40 | 63 | 57 | 58 | 26 | 24 | 27 | 35 | 77 | 68 | 78 |
| 40-50 | 18 | 18 | 17 | 16 | 16 | 15 | 14 | 23 | 22 | 12 |
| 50-60 | 24 | 5 | 4 | 8 | 6 | 3 | 13 | 3 | 19 | 26 |
| 60-70 | 6 | 2 | 1 | 12 | 10 | 5 | 9 | 6 | 15 | 7 |
| 70-80 | 42 | 44 | 37 | 22 | 27 | 38 | 37 | 58 | 42 | 54 |
| Всего | ||||||||||
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
Плотность распределения
а) абсолютная
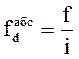 (1.1)
(1.1)
где f – частота интервала;
і – ширина интервала.
б) относительная
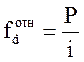 (1.2)
(1.2)
где Р- относительная частота интервала;
і – ширина интервала.
Мода
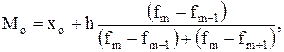 (1.3)
(1.3)
где хо – нижняя граница модального интервала;
h – ширина модального интервала;
fm – частота модального интервала (интервал с наибольшей частотой);
f m-1, f m+1 – частота предыдущего и последующего интервалов относительно модального.
Медиана
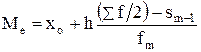 , (1.4)
, (1.4)
где хо – нижняя граница медианного интервала;
h – ширина медианного интервала;
S m-1 – кумулятивная частота интервала, предшествующего медианному;
fm – частота медианного интервала.
Асимметрия
Коэффициент асимметрии
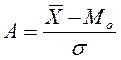 (1.5)
(1.5)
где Х – средняя взвешенная;
Мо – мода;
σ – среднее квадратическое отклонение;
Средняя взвешенная
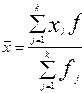 (1.6)
(1.6)
где хj – среднее значение признака в j-м интервале вариационного ряда;
fj – частота повторения признаков в j-м интервале вариационного ряда;
j – порядковый номер интервала вариационного ряда, j=1, 2, …, k.
Дисперсия для вариационного ряда
 |
A>0 – правосторонняя асимметрия;
A<0 – левосторонняя асимметрия.
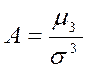 (1.8)
(1.8)
Момент третьего порядка
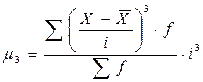 (1.9)
(1.9)
Критерии асимметрии:
A<0,25 – слабая асимметрия;
0,25<A<0,5 – средняя асимметрия;
A>0,5 – сильная асимметрия.
Эксцесс
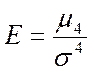 (1.10)
(1.10)
Момент четвертого порядка
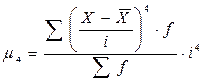 (1.11)
(1.11)
Критерии эксцесса:
Е=3 – симметричное распределение
Е<3 – плосковершинное распределение
Е>3 – островершинное распределение.
Пример решения
Таблица 1.2
Распределение работников предприятия по уровню заработной платы
| Месячная ЗП, ден. ед. | Количество рабочих | Плотность распределения | ||
| человек (f) | % (р) | человек | % | |
| 0 – 200 200 – 400 400 – 600 600 – 800 800 – 1200 | 34 52 72 70 30 | 13,2 20,2 27,9 27,1 11,6 | 0,17 0,26 0,36 0,35 0,04 | 0,066 0,101 0,140 0,136 0,017 |
| Итого | 258 | 100,0 | - | - |
На предприятии 72 человека или 27,9% получают ЗП от 400 до 600 ден. ед. из 258 сотрудников. Выплата ЗП на предприятии распределена таким образом, что с одной стороны, на каждую денежную единицу в интервале от 400 до 600 ден. ед. приходится 0,36 чел. или 0,14% от всей численности. С другой стороны, наименьшая плотность наблюдается в интервале от 800 до 1200 ден. ед. – 0,04 чел./ден. ед., 0,017% всей численности, при том, что ЗП в сумме 800-1200 ден. ед. получают 30 человек на предприятии.
Таблица 1.3
Расчет параметров асимметрии и эксцесса
| Количество поставок в месяц, шт | Размер партии поставки материалов, т | Xj | Xjfj | 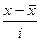
| 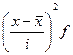
| 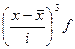
| 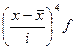
|
| 10-12 12-14 14-16 16-18 18-20 | 0,17 0,20 0,27 0,23 0,13 | 11 13 15 17 19 | 11,87 2,60 4,05 3,91 2,47 | -1,95 -1,95 0,05 1,05 20,5 | 0,6464 0,1805 0,0007 0,2536 0,5436 | -1,2605 -1,1715 0,00 0,2662 1,1200 | 2,4580 0,1629 0,00 0,2796 2,2959 |
| Итого | 1,00 | 14,9 | 1,6275 | -0,0458 | 5,1964 |
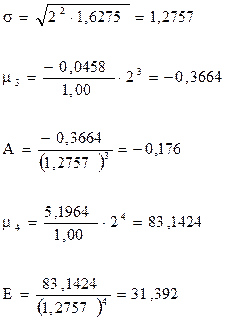
Распределение количества поставок по размеру партии поставок характеризуется слабой левосторонней ассиметрией (А<0 и А=0,176 <0,25) и выраженным островершинным распределением, т.к. Е=31,39 > 3.








