При определении потерь напора при внезапном сужении потока необходимо коэффициент умножить на бóльший скоростной напор, то есть на V2 /2×g.
Коэффициент местного сопротивления при внезапном расширении русла может быть определен по следующей аналитической зависимости:
 |
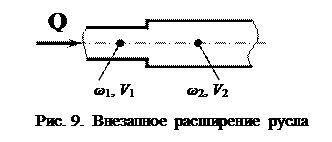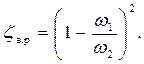(4)
При определении потерь напора при внезапном расширении потока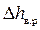 
необходимо коэффициент 
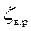умножить на бóльший скоростной напор, то есть на V1 /2×g.
Порядок выполнения работы
1. Перенести из табл. 9 лабораторной работы № 6 (см. Приложение) данные канала переменного сечения: значения площадей сечений II и III (внезапное сужение) и полных напоров в этих сечениях; значения площадей сечений IV и V (внезапное расширение) и полных напоров в этих сечениях, а также скоростных напоров в сечениях III и IV (при этом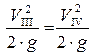 
) в табл. 10 (см. Приложение).
2. Определить опытные значения местных потерь при внезапном сужении потока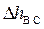 
как разность полных напоров сечений II и III соответственно.
3. Определить опытные значения местных потерь при внезапном расширении потока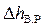 
как разность полных напоров сечений IV и V соответственно.
4. Найти расчетные значения местных потерь при внезапном сужении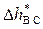 
и внезапном расширении 
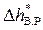потока, используя формулу Вейсбаха (1), также формулы (3) и (4) для определения коэффициентов местных сопротивлений при внезапном сужении и расширении русла соответственно.
5. Определить относительное расхождение d опытного и расчетного значений потерь напора при внезапном сужении и расширении русла.
6. Сделать выводы по лабораторной работе.
Работа 8. ОПРЕДЕЛЕНИЕ потерь напора по длине
Цель работы
1. Освоение экспериментального и расчетного методов определения потерь напора на трение по длине.
2. Проведение сравнительного анализа потерь напора по длине, полученных экспериментальным методом, с потерями напора, рассчитанными по формуле Дарси-Вейсбаха при использовании расчетных зависимостей для коэффициента гидравлического трения. Вычисление относительного расхождения экспериментального и расчетного значений потерь напора по длине.
Общие сведения
В случае установившегося движения жидкости при равномерном её течении эпюра скорости в поперечном сечении не изменяется вдоль потока. Возникающие при этом потери энергии на прямых участках трубопроводов и каналов с постоянными по длине сечениями называются потерями по длине, а гидравлическое сопротивление, вызывающее эти потери, – сопротивлением по длине. Таким образом, сопротивлением по длине называется сопротивление прямых участков трубопроводов и каналов с постоянными по длине сечениями при равномерном движении жидкости.
Потери по длине обусловлены внутренним трением в жидкости, поэтому имеют место не только в шероховатых, но и в гладких трубах и каналах. Физической причиной гидравлического трения является вязкость и инерционность жидкости. Таким образом, потери по длине обусловлены инерционно-вязкостными свойствами жидкости и шероховатостью стенок каналов и могут быть определены по формуле Дарси – Вейсбаха:
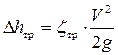, (1)
где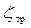 
– коэффициент сопротивления трения; 
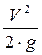– скоростной напор, рассчитанный по средней скорости V.
Коэффициент сопротивления трения 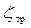зависит от размеров трубопроводов: возрастает с увеличением длины ℓ и уменьшается с увеличением поперечного сечения канала (диаметра d или гидравлического радиуса R, где R = w /П – отношение площади живого сечения w к смоченному периметру П):
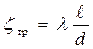– для круглых труб и каналов, (2)
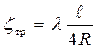– для остальных труб. (3)
Здесь l – коэффициент гидравлического трения, который зависит от числа Рейнольдса Re и относительной шероховатости стенок трубы или канала k, то есть
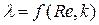. (4)
Число Рейнольдса для круглых труб и каналов
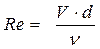, (5)
для каналов и труб произвольного сечения
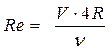, (6)
здесь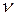 
– кинематический коэффициент вязкости, м2/с.
Относительная шероховатость k представляет собой отношение абсолютной эквивалентной шероховатости Δ к диаметру d, то есть
k = Δ/d. (7)
По числу Рейнольдса вся область сопротивления разбита на пять зон.
I зона ( Re ≤ 2000) – зона ламинарного режима течения.
При ламинарном движении коэффициент гидравлического трения l практически не зависит от шероховатости, являясь функцией только числа Рейнольдса, то есть l I = f ( Re ), и определяется формулой Пуазейля:
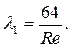(8)