Санкт-Петербургский государственный экономический университет (СПбГЭУ)
Министерство образования и науки Российской Федерации
Национальный исследовательский университет ИТМО
(Университет ИТМО)
Региональная студенческая
математическая олимпиада
Санкт-Петербурга
2022 г.

Санкт-Петербург
2022
В 2000-2022 гг. студенческая олимпиада г. Санкт-Петербурга по математике проводилась Национальным исследовательским университетом ИТМО (до 2019 года носившим название Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, а до 2011 - Санкт-Петербургский государственный университет информационных технологий, механики и оптики, СПбГУ ИТМО). В 2022 году каждый вуз мог выставить на олимпиаду одну команду из трех человек (в командный зачет входили все участники команды) и студентов в личный зачет. В личном зачете участвовали все заявленные студенты. Результат вуза в командном зачете определялся по результату его команды.
Олимпиада проводилась в воскресенье 23 октября 2022 года. На решение задач отводилось 4 часа. Пользоваться печатными или электронными справочниками не разрешалось. Студентам всех групп было предложено 9 задач. Каждая задача оценивалась в 10 баллов.
Председателем жюри был профессор Н.А.Широков. В оргкомитет олимпиады входили: проректор Университета ИТМО д.т.н., проф. Никифоров В.О., зам. Нач. ДНИиР Студеникин Л.М., нач. ДОД Багаутдинова А.Ш., директор УЦСНКиВ Елисеев О.В.,, руководитель СПИБ Юшков Е.Ю., проф., д.ф.-м.н Попов И.Ю., PhD, н.с. Аксенов В.Е., доц., к.т.н. Блинова И.В., к.ф.-м.н. Трифанова Е.С., к.ф.-м.н. Трифанов А.И, доц.., к.ф.-м.н. Попов А.И.; к.т.н. Правдин К.В., к.ф.-м.н. Бойцев А.А., вед. инж. Коченюк Т.Г.
Составители: проф., д.ф.-м.н. Широков Н.А., д.ф.-м.н. Попов И.Ю.; доц., к.ф.-м.н. Трифанова Е.С., к.т.н. Блинова И.В., к.ф.-м.н. Трифанов А.И., к.ф.-м.н. Попов А.И., к.т.н. Правдин К.В., PhD Аксенов В.Е., асс. Бабушкин М.В.
Задачи региональной олимпиады студентов вузов Санкт-Петербурга 23.10.2022
1.Даны векторы 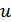 ,
, 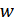 и
и 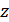 длины 1 на плоскости. Докажите, что можно подобрать знаки так, что
длины 1 на плоскости. Докажите, что можно подобрать знаки так, что 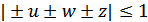 .
.
2. Вычислить определитель порядка 2022, общий элемент которого 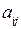
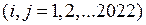 равен числу делителей наибольшего общего делителя чисел
равен числу делителей наибольшего общего делителя чисел 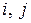 .
.
3. Вычислить интеграл 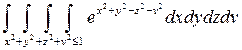 .
.
4. Пусть бесконечный в обоих направлениях ряд 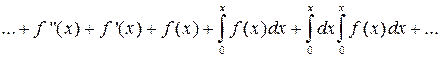 сходится равномерно на (-1,1). Какую функцию он представляет?
сходится равномерно на (-1,1). Какую функцию он представляет?
5. Пусть все корни вещественного полинома 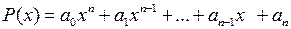 имеют первую кратность и среди них
имеют первую кратность и среди них 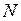 положительных. Пусть
положительных. Пусть 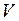 число перемен знака в последовательности
число перемен знака в последовательности 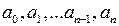 коэффициентов полинома. Доказать, что
коэффициентов полинома. Доказать, что 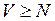
6. Пусть гладкая функция 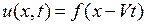 , где
, где 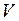 не зависит от
не зависит от 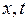 , является при
, является при 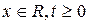 , решением уравнения
, решением уравнения 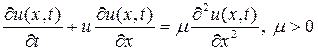 и удовлетворяет условиям
и удовлетворяет условиям 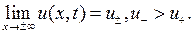
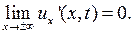 Найти
Найти 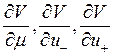 .
.
7. Найти все непрерывные функции 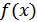 ,
, 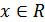 , если
, если 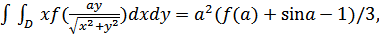
при всех 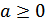 ,
, 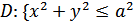 ,
, 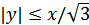 ,
, 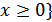 .
.
8. Прозрачный двугорбый верблюд стоит на экваторе в ясный полдень, когда солнце в зените. Поверхность спины верблюда описывается уравнением 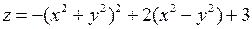 . На спине в точке
. На спине в точке 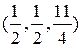 сидит гусеница. Желая получше оглядеть окрестности, она решает заползти на вершину ближайшего горба. При переползании гусеница все время движется в направлении наибыстрейшего увеличения высоты, наблюдает за движением ее тени на плоской горизонтальной поверхности земли
сидит гусеница. Желая получше оглядеть окрестности, она решает заползти на вершину ближайшего горба. При переползании гусеница все время движется в направлении наибыстрейшего увеличения высоты, наблюдает за движением ее тени на плоской горизонтальной поверхности земли 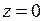 и размышляет; «А существует ли пара точек на плоскости
и размышляет; «А существует ли пара точек на плоскости 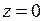 таких, что разность расстояний от точки моей тени до каждой из этих точек не меняется при моем движении?». Ответьте на вопрос гусеницы и объясните ответ. Считать, что при прохождении через верблюда свет не преломляется.
таких, что разность расстояний от точки моей тени до каждой из этих точек не меняется при моем движении?». Ответьте на вопрос гусеницы и объясните ответ. Считать, что при прохождении через верблюда свет не преломляется.
9. Дана непрерывная функция 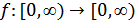 такая, что существует натуральное
такая, что существует натуральное 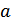 , что
, что 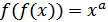 для всех
для всех 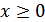 . Докажите, что
. Докажите, что 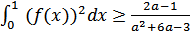 .
.
Решения
1. Решение. Отложим все векторы от центра O. Если концы не составляют треугольник с острыми углами, тогда они все лежат на одной половине окружности радиусом 1 с центром О. Отразим один вектор (центральный) и получим остроугольный треугольник. Пусть новыми векторами будут 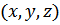 --- где два вектора из ·
--- где два вектора из · 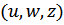 с плюсом, а один с минусом (тот, что отражен). Пусть
с плюсом, а один с минусом (тот, что отражен). Пусть 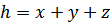 . Найдем скалярные произведения:
. Найдем скалярные произведения: 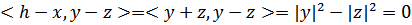 ,
, 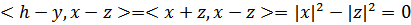 ,
, 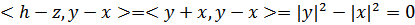 . Тем самым, точка
. Тем самым, точка 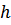 является центром пересечения высот остроугольного треугольника, а, значит, лежит внутри описанной окружности радиуса 1.
является центром пересечения высот остроугольного треугольника, а, значит, лежит внутри описанной окружности радиуса 1.
2. Ответ:. 1.
Решение. Пусть 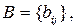 где
где 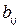 равен 1, если
равен 1, если 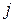 делитель
делитель 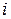 , то есть это треугольная матрица с единицами на диагонали. Тогда матрица
, то есть это треугольная матрица с единицами на диагонали. Тогда матрица 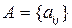 будет равна
будет равна 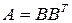 , где
, где 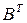 - транспонированная матрица. Тогда
- транспонированная матрица. Тогда 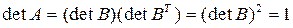 ..
..
3. Ответ: 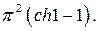
Решение.
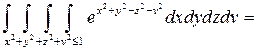
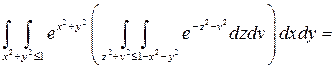
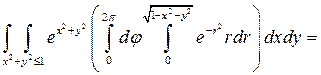
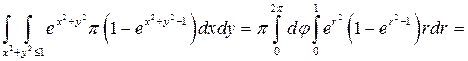
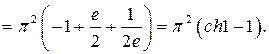 .
.
4. Ответ: . 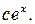
Решение. Обозначим сумму ряда 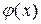 . Поскольку ряд сходится равномерно, его можно почленно дифференцировать. Но тогда
. Поскольку ряд сходится равномерно, его можно почленно дифференцировать. Но тогда 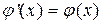 . Значит,
. Значит, 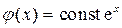 .
.
5. Решение. Пусть 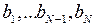 положительные корни полинома
положительные корни полинома 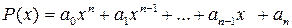 . Полином можно представить в виде
. Полином можно представить в виде 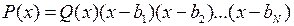 ,
,
где 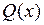 полином степени
полином степени 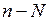 с вещественными коэффициентами. У
с вещественными коэффициентами. У 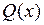 количество перемен знака у коэффициентов не меньше нуля, соответственно, у
количество перемен знака у коэффициентов не меньше нуля, соответственно, у 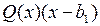 оно не меньше 1. Поясним это. Рассмотрим
оно не меньше 1. Поясним это. Рассмотрим 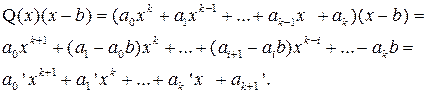
Умножение на -1 не меняет количество перемен знака, поэтому можно считать, что 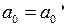 положительно. Если в последовательности
положительно. Если в последовательности 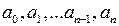 на каком-то месте происходит смена знака, например,
на каком-то месте происходит смена знака, например, 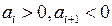 , то у последовательности
, то у последовательности 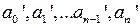 на соответствующем месте тоже появится другой знак
на соответствующем месте тоже появится другой знак 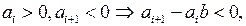 так как
так как 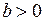 , то есть количество изменений знака не уменьшится, да еще добавляется коэффициент
, то есть количество изменений знака не уменьшится, да еще добавляется коэффициент 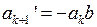 c добавочным изменением знака, то есть количество изменений знака увеличится хотя бы на 1.
c добавочным изменением знака, то есть количество изменений знака увеличится хотя бы на 1.
Далее, у 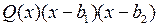 количество изменений знака не меньше 2, и так далее, наконец, у
количество изменений знака не меньше 2, и так далее, наконец, у 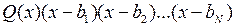 оно не меньше
оно не меньше 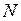 , что и требовалось доказать.
, что и требовалось доказать.
6. Ответ. 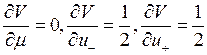
Решение. Введем переменную 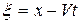 . После подстановки функции в уравнение получим обыкновенное дифференциальное уравнение для функции
. После подстановки функции в уравнение получим обыкновенное дифференциальное уравнение для функции 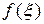 :
: 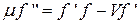 . Проинтегрируем уравнение по всей оси, получим
. Проинтегрируем уравнение по всей оси, получим
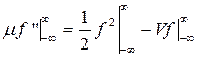 . Поскольку
. Поскольку 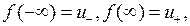 имеем
имеем 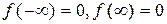 . Значит,
. Значит, 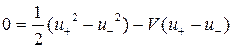 . Отсюда получаем
. Отсюда получаем 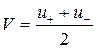 . Значит
. Значит 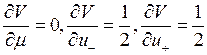 .
.
7. Ответ: 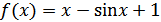 .
.
Решение. Обозначим интеграл 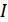 . Переходя к полярным координатам, получаем
. Переходя к полярным координатам, получаем 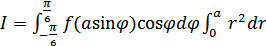 . Полагая
. Полагая 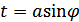 , имеем
, имеем 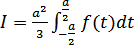 . Тогда равенство (1) принимает вид
. Тогда равенство (1) принимает вид
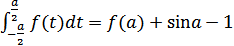 (2)
(2)
Дифференцируя обе части равенства (2) по 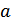 , приходим к уравнению
, приходим к уравнению
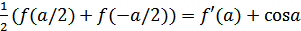 (3)
(3)
Из (3) 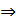
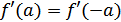 , или
, или 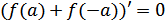
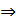
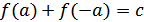 .
.
С учетом условия 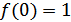 , вытекающего из (2), получаем
, вытекающего из (2), получаем 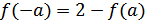 . Тогда из (3) находим
. Тогда из (3) находим 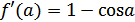
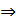
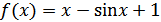 .
.
8. Ответ: Существует.
Решение. По условию задачи тень движется по плоскости 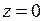 ортогонально линиям уровня функции
ортогонально линиям уровня функции 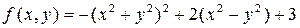 , то есть по направлению
, то есть по направлению 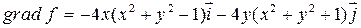 . Покажем, что линия
. Покажем, что линия 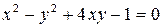 является траекторией тени гусеницы. Удобно преобразовать его к виду
является траекторией тени гусеницы. Удобно преобразовать его к виду 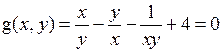 . Кривая проходит через точку
. Кривая проходит через точку 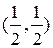 . Осталось проверить ортогональность градиентов:
. Осталось проверить ортогональность градиентов: 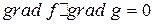 .
. 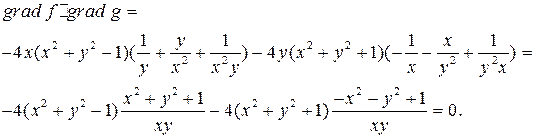
Кривая 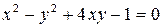 является гиперболой, у которой искомая пара точек существует.
является гиперболой, у которой искомая пара точек существует.
9. Решение. Покажем, что отображение взаимно однозначно. Если 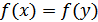 ,то
,то 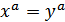 и, тем самым,
и, тем самым, 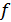 --- биекция. Так как
--- биекция. Так как 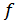 непрерывная, то она либо строго возрастающая, либо строго убывающая. Допустим, она убывает. Тогда
непрерывная, то она либо строго возрастающая, либо строго убывающая. Допустим, она убывает. Тогда 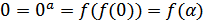 .Тогда для любого
.Тогда для любого 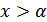 функция отрицательная. Противоречие. Поэтому
функция отрицательная. Противоречие. Поэтому 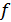 получается строго возрастающей. Теперь найдем
получается строго возрастающей. Теперь найдем 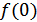 . Пусть
. Пусть 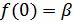 . Тогда,
. Тогда, 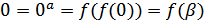 .. С другой стороны,
.. С другой стороны, 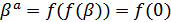 .. Получается, что
.. Получается, что 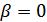 или
или 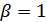 . Пусть
. Пусть 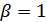 , тогда
, тогда 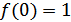 и
и 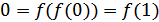 ,, что противоречит возрастанию
,, что противоречит возрастанию 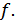 Поэтому
Поэтому 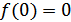 . Так как функция обратима, то получим
. Так как функция обратима, то получим 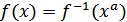 . Поэтому
. Поэтому 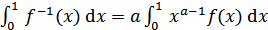 .
.
Применяя неравенство Янга для возрастающей функции, получаем:
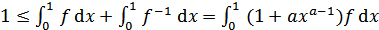 .
.
Применяя теперь неравенство Коши-Шварца, получаем для правой части неравенства:
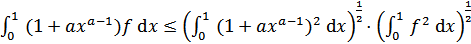 .
.
Отсюда
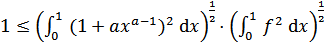 .
.
Вычисляя первый из интегралов в правой части и возводя неравенство в квадрат, приходим к искомому неравенству.
Количество участников, решивших задачи (определено по формуле: полная сумма набранных всеми участниками баллов за задачу, деленная на 10 (стоимость задачи)).
| № задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Кол-во решивших | 35,2 | 8,3 | 11,9 | 21,4 | 13,0 | 1,6 | 8,1 | 6,3 | 3,8 |
В олимпиаде приняли участие студенты следующих университетов:
Университет ИТМО
Санкт-Петербургский государственный экономический университет (СПбГЭУ)
Военная академия связи имени С.М. Буденного (ВАС)
Санкт-Петербургский государственный университет аэрокосмического приборостроения (ГУАП)
Государственный университет морского и речного флота им. адм. С.О. Макарова (ГУМРФ)
Военно-космическая академия им. А. Ф. Можайского (ВКА)
Военный институт (инженерно-технический) (ВИИТ)
Санкт-Петербургский государственный университет (СПбГУ)
Санкт-Петербургский горный университет
Балтийский государственный технический университет "Военмех" им. Д.Ф. Устинова (БГТУ, ВОЕНМЕХ)
Санкт-Петербургский государственный электротехнический университет "ЛЭТИ имени В.И.Ульянова (ЛЭТИ)"
Санкт-Петербургский государственный технологический институт (технический университет (ТИ)
Санкт-Петербургский политехнический университет Петра Великого (СПбГПУ)
Российский государственный педагогический университет им. А.И.Герцена (РГПУ)
Санкт-Петербургский государственный архитектурно-строительный университет (СПбГАСУ)
Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича(СПбГУТ)
Национальный исследовательский университет "Высшая школа экономики", Санкт-Петербургский филиал (ВШЭ)
Российский государственный гидрометеорологический университет
Санкт-Петербургский университет Государственной противопожарной службы Министерства РФ по делам гражданской обороны, чрезвычайным ситуациями ликвидации последствий стихийных действий (УГПС МЧС)
Результаты в командном зачете:
| I группа | II группа | III группа |
| 1. ИТМО – 107 2 . СПбПУ- 41 3 . ВШЭ – 29 4.РГПУ – 12 | 1. ВКА – 79 2. ЛЭТИ – 20 3. БГТУ – 19 4. ГУАП – 7 5. СПбГУТ – 6 | 1. СПбГЭУ – 16 2. ВИ(ИТ) – 14 3. РГГМУ – 14 4. ГУМРФ - 14 5. ВАС-7 6. Горный – 5 7. МЧС- 0 |
Результаты участников, вошедших в командный зачет
I группа
ИТМО
СПбПУ
ВШЭ
РГПУ
| II группа
ВКА
ЛЭТИ
БГТУ
ГУАП
СПбГУТ
| III группа
СПбГЭУ
ВИ(ИТ)
РГГМУ
ГУМРФ
ВАС
Горный
УГПС МЧС
|
Личное первенство:
I группа
| № | ФИО | ВУЗ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Σ | Дип лом |
| 1 | Яковлев Захар Александрович | ИТМО | 10 | 0 | 10 | 7 | 9 | 10 | 10 | 10 | 2 | 68 | I |
| 2 | Москаленко Тимофей Дмитриевич | СПбГУ | 10 | 10 | 2 | 10 | 9 | 0 | 0 | 6 | 0 | 47 | II |
| 3 | Хамзин Виктор Олегович | СПбГУ | 10 | 0 | 10 | 10 | 10 | 0 | 5 | 2 | 0 | 47 | II |
| 4 | Власов Алексей Андреевич | СПбГУ | 10 | 2 | 10 | 10 | 9 | 0 | 0 | 5 | 0 | 46 | II |
| 5 | Шарафетдинова Галия Маратовна | СПбГУ | 10 | 0 | 1 | 10 | 9 | 0 | 0 | 10 | 0 | 40 | II |
| 6 | Борозенец Николай Евгеньевич | СПбГУ | 4 | 0 | 10 | 10 | 9 | 0 | 3 | 0 | 0 | 36 | III |
| 7 | Миргалимова Розалина Зуфаровна | СПбГУ | 2 | 8 | 0 | 10 | 9 | 0 | 0 | 0 | 5 | 34 | III |
| 8 | Орешников Даниил Михайлович | ИТМО | 10 | 1 | 0 | 10 | 9 | 0 | 0 | 0 | 0 | 30 | III |
| 9 | Глазков Михаил Сергеевич | СПбГУ | 10 | 0 | 9 | 10 | 0 | 0 | 0 | 0 | 0 | 29 | III |
| 10 | Ладный Кирилл Сергеевич | СПбГУ | 2 | 0 | 10 | 9 | 3 | 0 | 5 | 0 | 0 | 29 | III |
| 11 | Денисов Никита Викторович | НИУ ВШЭ | 10 | 7 | 6 | 3 | 0 | 0 | 0 | 1 | 0 | 27 | III |
| 12 | Дружков Сергей Александрович | СПбГУ | 8 | 0 | 1 | 0 | 10 | 2 | 0 | 1 | 5 | 27 | III |
| 13 | Пакульневич Константин Михайлович | ИТМО | 10 | 4 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 23 | III |
| 14 | Красников Роман Андреевич | СПбПУ | 0 | 0 | 10 | 9 | 0 | 0 | 3 | 0 | 0 | 22 | III |
| 15 | Коротченко Таисия Сергеевна | СПбГУ | 4 | 3 | 0 | 4 | 9 | 0 | 0 | 0 | 0 | 20 | III |
| 16 | Скворцов Артем Андреевич | СПбГУ | 1 | 1 | 1 | 10 | 2 | 0 | 5 | 0 | 0 | 20 | III |
II группа
| № | ФИО | ВУЗ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Σ | Дип лом |
| 1 | Ковальчук Владимир Сергеевич | ВКА | 10 | 0 | 10 | 10 | 0 | 0 | 9 | 2 | 0 | 41 | I |
| 2 | Козлов Виктор Владимирович | ВКА | 10 | 5 | 1 | 1 | 0 | 0 | 8 | 0 | 0 | 25 | II |
| 3 | Полетаев Марк Валерьевич | ВКА | 9 | 0 | 0 | 7 | 0 | 0 | 2 | 0 | 0 | 18 | II |
| 4 | Иванов Серафим Кириллович | ЛЭТИ | 6 | 0 | 2 | 10 | 0 | 0 | 0 | 0 | 0 | 18 | II |
| 5 | Бояркина Юлия Владимировна | БГТУ | 10 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 14 | III |
| 6 | Давыденко Владислав Сергеевич | ВКА | 4 | 2 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 13 | III |
| 7 | Бабух Вадим Алексеевич | ВКА | 1 | 1 | 0 | 7 | 0 | 0 | 3 | 0 | 1 | 13 | III |
| 8 | Акименко Полина Дмитриевна | СПбГУТ | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | III |
III группа
| № | ФИО | ВУЗ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Σ | Дип Лом |
| 1 | Баранов Виктор Михайлович | СПбГЭУ | 4 | 1 | 0 | 0 | 0 | 0 | 4 | 2 | 0 | 11 | II |
| 2 | Романов Александр Дмитриевич | СПбГЭУ | 3 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 5 | 11 | II |
| 3 | Кузьмин Алексей Вадимович | ГУМРФ | 1 | 4 | 0 | 0 | 0 | 0 | 3 | 1 | 0 | 9 | II |
| 4 | Гизатуллин Радмир Загитович | ВИ(ИТ) | 3 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 8 | II |








