Медиана треугольника.
1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины треугольника.
2. Медиана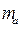 
, проведенная к стороне а треугольника с длинами сторон а , b и с, находится по формуле:
.
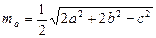3. Медиана делит треугольник на две части с равными площадями. Три медианы делят треугольник на шесть треугольников с равными площадями.
4. Если 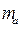и 
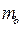- медианы треугольника, а 
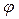- угол между ними, то площадь треугольника находится по формуле:
.
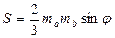5. Из медиан любого треугольника можно составить новый треугольник, площадь которого составляет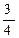 
от площади исходного.
Задачи для самостоятельного решения.
1. В равнобедренном треугольнике АВС (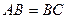 
) расстояние от вершины В до точки пересечения медиан равно 6 см. Найти расстояние от середины боковой стороны до основания треугольника. Ответ: 4,5 см.
2. В равнобедренном треугольнике КРМ (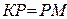 
) расстояние от вершины Р до точки пересечения медиан равно 14 см. Найти расстояние от середины боковой стороны до основания треугольника. Ответ: 10,5 см.
3. Боковая сторона равнобедренного треугольника равна 5 см, а основание — 3 см. Найдите медиану треугольника, проведенную к его боковой стороне. Ответ: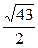 
см.
4. Боковая сторона равнобедренного треугольника равна 7 см, а основание — 3 см. Найдите медиану треугольника, проведенную к его боковой стороне. Ответ: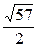 
см.
5. Стороны треугольника равны соответственно 11 см, 12 см и 13 см. Найдите медиану, проведенную к наибольшей стороне треугольника. Ответ: 9,5 см.
6. Стороны треугольника равны 8 см, 9 см и 13 см. Найдите медиану треугольника, проведенную к его наибольшей стороне. Ответ: 5,5 см.
7. Стороны треугольника равны 6 см, 10 см и 12 см. Найдите медиану треугольника, проведенную к его наименьшей стороне. Ответ: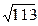 
см.
8. Стороны треугольника равны 8 см, 12 см и 16 см. Найдите медиану треугольника, проведенную к его наименьшей стороне. Ответ: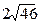 
см.
9. Стороны треугольника равны 4 см, 6 см и 8 см. Найдите медиану треугольника, проведенную к его средней по величине стороне. Ответ: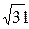 
см.
10. Стороны треугольника равны 13 см, 14 см и 15 см. Найдите медиану треугольника, проведенную к его средней по величине стороне. Ответ: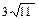 
см.
11. Две стороны треугольника равны 7 см и 11 см. Медиана треугольника, проведенная к его третьей стороне, равна 6 см. Найдите неизвестную сторону треугольника.
Ответ: 14 см.
12. Две стороны треугольника равны 16 см и 18 см. Медиана треугольника, проведенная к его третьей стороне, равна 11 см. Найдите неизвестную сторону треугольника.
Ответ: 26 см.
13. Две стороны треугольника равны 6 см и 8 см. Медиана треугольника, проведенная к его третьей стороне, равна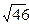 
см. Найдите неизвестную сторону треугольника.
Ответ: 4 см.
14. Две стороны треугольника равны 5 см и 7 см. Медиана треугольника, проведенная к его третьей стороне, равна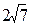 
см. Найдите неизвестную сторону треугольника.
Ответ: 6 см.
15. Основание равнобедренного треугольника равно 10 см, а медиана, проведенная к боковой стороне, равна 8 см. Найти боковую сторону треугольника. Ответ: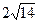 
см.
16. Основание равнобедренного треугольника равно 7 см, а медиана, проведенная к боковой стороне, тоже равна 7 см. Найти боковую сторону треугольника. Ответ: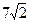 
см.
17. В треугольнике АВС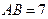 
см,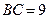 
см, ВМ – медиана. Найти сторону АС, если 
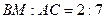. Ответ: 14 см.
18. В треугольнике АВС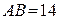 
см,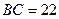 
см, ВМ – медиана. Найти сторону АС, если 
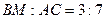. Ответ: 28 см.
19. В треугольнике АВС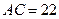 
см,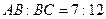 
см, а медиана АК равна 14 см. Найти стороны АВ и ВС. Ответ: 14 см и 24 см.
20. В треугольнике АВС 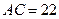см,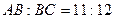 
см, а медиана АК равна 18 см. Найти стороны АВ и ВС. Ответ: 22 см и 24 см.
21. В прямоугольном треугольнике медианы катетов равны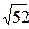 
см и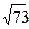 
см. Найти площадь треугольника. Ответ: 24 см 
.
22. В прямоугольном треугольнике медианы катетов равны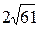 
см и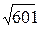 
см. Найти площадь треугольника. Ответ: 120 см .
23. Две стороны треугольника равны 14 см и 48 см. Медианы, проведенные к этим сторонам, взаимно перпендикулярны. Найти третью сторону треугольника. Ответ: 10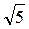 
см.
24. Две стороны треугольника равны 6 см и 8 см. Медианы, проведенные к этим сторонам, взаимно перпендикулярны. Найти третью сторону треугольника. Ответ: 2 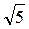см.
25. Площадь треугольника ABC равна 40 см . На медиане AM отметили точку P такую, что AР:PM = 2:3. Найдите площадь треугольника BPM. Ответ: 12 см .
26. Площадь треугольника ABC равна 52 см . На медиане AM отметили точку P такую, что AР:PM = 5:8. Найдите площадь треугольника АPВ. Ответ: 10 см .
27. На медиане BD треугольника ABC отметили точку M так, что BM:MD = 3:1. Найдите площадь треугольника ABC, если площадь треугольника AMD равна 3 см . Ответ: 24 см .
28. На медиане BD треугольника ABC отметили точку M так, что BM:MD = 4:5. Найдите площадь треугольника ABC, если площадь треугольника AВM равна 4 см . Ответ: 18 см .
29. В треугольнике АВС G – точка пересечения медиан, а длины медиан АК и ВМ равны 7 см и 12 см соответственно. Найти площадь треугольника АВС, если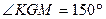 
. Ответ: 28 см .
30. В треугольнике АВС G – точка пересечения медиан, а длины медиан АК и ВМ равны 9 см и 11 см соответственно. Найти площадь треугольника АВС, если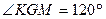 
.
Ответ: 33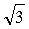 
см .
31. Известно, что площадь треугольника равна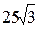 
см , а две его медианы имеют длины 5 см и 15 см соответственно. Найти угол между этими медианами. Ответ: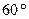 
.
32. Известно, что площадь треугольника равна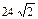 
см , а две его медианы имеют длины 4 см и 18 см соответственно. Найти угол между этими медианами. Ответ: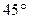 
.
33. Две медианы треугольника перпендикулярны друг другу, причем их длины относятся как 3:7. Найти длины этих медиан, если площадь треугольника равна 126 см .
Ответ: 9 см и 21 см.
34. Две медианы треугольника перпендикулярны друг другу, причем их длины относятся как 4:5. Найти длины этих медиан, если площадь треугольника равна 120 см .
Ответ: 12 см и 15 см.
35. Одна из медиан треугольника равна 10 см и образует угол 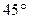со второй медианой. Чему равна вторая медиана, если площадь треугольника равна 
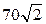см . Ответ: 21 см.
36. Одна из медиан треугольника равна 8 см и образует угол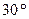 
со второй медианой. Чему равна вторая медиана, если площадь треугольника равна 40 см . Ответ: 15 см.
37. Основание треугольника равно 14 см, а медианы, проведенные к боковым сторонам, -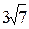 
см и 
см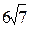. Найти площадь треугольника. Ответ: 
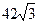см .
38. Основание треугольника равно 14 см, а медианы, проведенные к боковым сторонам, - 9 см и 15 см. Найти площадь треугольника. Ответ: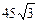 
см .
39. Основание треугольника равно 26 см. Медианы боковых сторон равны 30 см и 39 см. Найти площадь треугольника. Ответ: 720 см .
40. Основание треугольника равно 10. Медианы боковых сторон равны 18 см и 15 см. Найти площадь треугольника. Ответ: 144 см .
41. В треугольнике АВС с площадью 42 см биссектриса АМ делит медиану ВЕ в отношении ВК:КЕ = 2. Найти площадь четырехугольника ЕКМС. Ответ: 14 см .
42. В треугольнике АВС биссектриса АМ делит медиану ВЕ в отношении ВК:КЕ = 2. Найти площадь треугольника АВС, если площадь четырехугольника ЕКМС равна 29 см .
Ответ: 87 см .
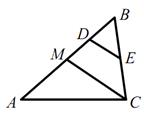
43. Отрезок CM — медиана треугольника ABC, изображенного на рисунке, отрезок DE — средняя линия треугольника MBC. Чему равна площадь четырехугольника MDEC, если площадь треугольника ABC равна 48 см ? Ответ: 18 см .
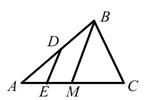44. Отрезок BM — медиана треугольника ABC, изображенного на рисунке, отрезок DE — средняя линия треугольника ABM. Чему равна площадь треугольника ABC, если площадь четырехугольника DBME равна 12 см ? Ответ: 32 см .
45. Медианы треугольника равны 13 см, 14 см и 15 см. Найти площадь треугольника. Ответ: 112 см .
46. Медианы треугольника равны 25 см, 17 см и 28 см. Найти площадь треугольника.
Ответ: 280 см .
47. Стороны треугольника равны 13 см, 20 см и 21 см. Найти площадь треугольника, составленного из медиан исходного. Ответ: 94,5 см .
48. Стороны треугольника равны 40 см, 39 см и 25 см. Найти площадь треугольника, составленного из медиан исходного. Ответ: 351 см .
49. В треугольнике MNP угол N – прямой,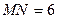 
см,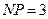 
см. Точка К лежит на стороне МР, А и В – точки пересечения медиан соответственно в треугольниках MNK и KNP. Найти площадь треугольника NAB. Ответ: 2 см .
50. В треугольнике MNP угол N – прямой,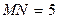 
см,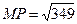 
см. Точка К лежит на стороне МР, А и В – точки пересечения медиан соответственно в треугольниках MNK и KNP. Найти площадь треугольника NAB. Ответ: 20 см .