«Анализ финансово-хозяйственной деятельности
Лабораторная работа №1
по дисциплине
«Анализ финансово-хозяйственной деятельности
 |
1. Факторный анализ. Оценка влияния факторов
1.1. Основные модели
детерминированного факторного анализа
Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.
В общем виде детерминированную модель можно представить в виде функции нескольких переменных:
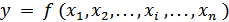
Введем обозначения:
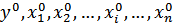− значения переменных в базисном периоде;
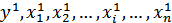− значения переменных в текущем (отчетном, фактическом) периоде;
Задача детерминированного факторного анализа заключается в количественной оценке влияния каждого фактора на изменение результативного показателя.
Иными словами, необходимо численно определить величины Δy(xi) (i = 1, 2,…, n), показывающие изменения результативного показателя y в отчетном периоде по сравнению с базисным вызванные изменением отдельных факторов xi.
Результаты детерминированного факторного анализа удобно представить в виде таблицы.
Таблица 1.1 - Результаты детерминированного факторного анализа
| Показатель | Значение | Удельный вес (%) | |
| 1 | Аргумент x1 |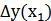 
| |
| 2 | Аргумент x2 |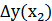 
| |
| 3 | … | … | |
| 4 | Аргумент xn |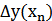 
| |
| Итого |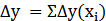 
| 100% |
Отметим, что должно выполняться равенство 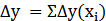, означающее, что сумма изменений результативного показателя y, вызванных изменением каждого фактора ( 
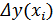) должна быть равна изменению результативного показателя ( 
).
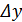Применяемые в анализе факторные модели можно свести к четырем типам: аддитивные, мультипликативные, кратные, смешанные, в которых исследуемый (результативный) показатель представлен в виде произведения, частного от деления или алгебраической суммы показателей, являющихся факторами детерминированной модели.
Аддитивные модели представляют собой алгебраическую сумму показателей и записываются следующим образом:
;
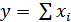Мультипликативная модель представляет собой произведение факторов.
В обобщенном виде она может быть представлена формулой:
;
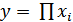Кратные модели представляют собой отношение факторов:
;
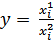Смешанные модели представляют собой комбинацию перечисленных моделей, например
;
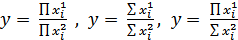В общем случае процедура детерминированного факторного анализа включает следующие этапы:
1) построение экономически обоснованной (с позиций факторного анализа) детерминированной факторной модели;
2) выбор способа анализа и подготовка условий для его выполнения;
3) реализация счетных процедур;
4) формулирование выводов.
1.2. Способы оценки влияния факторов
в детерминированном факторном анализе
Наиболее распространенными способами факторного детерминированного анализа являются метод цепной подстановки и его модификация − способ абсолютных разниц; способ простого прибавления неразложимого остатка; логарифмический способ долевого участия, интегральный, индексный. Выбор способа изучения факторной модели определяется его преимуществами перед остальными в каждой конкретной ситуации и в применении к конкретным аналитическим задачам.
Способ цепных подстановок. Этот способ заключается в определении ряда промежуточных значений результативного (обобщающего) показателя путем последовательной замены базисных значений факторов на отчетные. Разность промежуточных значений равна изменению результативного показателя за счет заменяемого фактора. Алгоритм применения способа цепных подстановок задается следующими соотношениями:
;
;
;
;
;
……………………………………………..
;
;
……………………………………………..
;
;
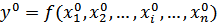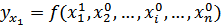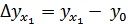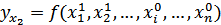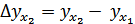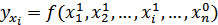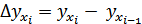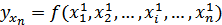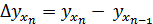где «нулевые» значения (индекс «0») - базисные значения факторов,
«единичные» (индекс «1») - фактические (отчетные) значения факторов;
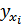- промежуточное значение результативного показателя.
Общее изменение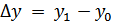 
складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
.
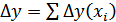Число расчетов результативного показателя на единицу больше числа измеряемых факторов. Преимущества данного способа: универсальность применения (применяется в анализе любых типов моделей), достаточная простота применения.
Однако этот метод имеет существенный недостаток − результаты факторного разложения зависят от выбранного порядка замены факторов.
В результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. Но в практических расчетах точностью оценки влияния факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Существуют некоторые правила, определяющие последовательность подстановки:
• при наличии в факторной модели количественных и качественных показателей в первую очередь производится подстановка количественных факторов;
• если модель представлена несколькими количественными или качественными показателями, последовательность подстановки определяется путем логического анализа.
Способ разниц применим в случае анализа мультипликативных моделей. Например, для модели типа
,
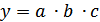Алгоритм решения принимает вид:
Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:
;
;
;
;
;
.
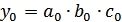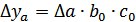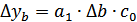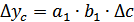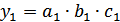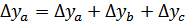Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида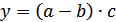 
.
Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.
Для мультипликативных моделей типа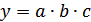 
методика анализа следующая:
- находят относительное отклонение каждого факторного показателя;
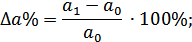
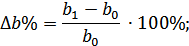
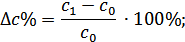
- определяют отклонение результативного показателя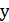 
за счет каждого фактора;
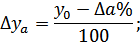
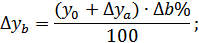
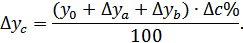
Метод дифференцирования основан на применении дифференциалов. Дифференциал – главная часть приращения функции относительно приращения аргументов.
Алгоритм применения метода дифференцирования:
1. определяется вид функции, устанавливающей связь показателя и факторов-аргументов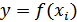 
;
2. находятся частные производные этой функции по каждому из факторов-аргументов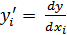 
;
3. рассчитываются значения частных производных при базисном значении факторов-аргументов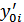 
;
4. рассчитываются приращения (абсолютные изменения) факторов аргументов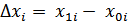 
;
5. определяется влияние изменения каждого из факторов-аргументов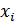 
на изменение результативного показателя 
;
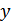6. определяется совместное влияние изменения всех факторов-аргументов на изменение результативного показателя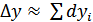 
.
Так как последнее равенство является приближенным, то при использовании метода дифференцирования возникает ошибка разложения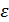 
(«неразложимый остаток»).
Задача распределения величины ошибки между отдельными факторами решается с применением различных методов. Наиболее простые и часто применимые – метод прибавления и деления неразложимого остатка.
Прием простого прибавления неразложимого остатка заключается в прибавлении величины ошибки к величине влияния одного из факторов (чаще всего качественного).
Прием деления неразложимого остатка предполагает равное деление величины ошибки («неразложимого остатка») между всеми факторами и прибавление результата к величине влияния каждого из факторов.
Логарифмический метод позволяет определить влияние не только двух, но и большего количества факторов на результативный показатель. В данном способе автоматически достигается пропорциональное распределение остатка по факторам.
Способ применим к кратным и мультипликативным моделям.
Мультипликативная факторная модель имеет вид
.
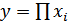Логарифмический способ основан на логарифмировании отклонения отчетного и базисного значений результативного признака, равного отношению соответствующих произведений факторов
.
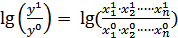Доля 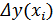фактора 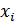в общем итоге 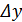определяется из соотношений
;
;
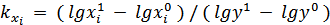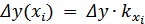Таким образом, при помощи коэффициентов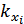 
производится пропорциональное распределение совокупного отклонения между факторами.
Например, для двухфакторной мультипликативной модели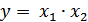 
, факторный анализ на основе логарифмического метода будет выглядеть следующим образом:
;
;
;
.
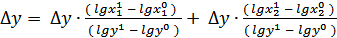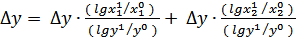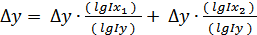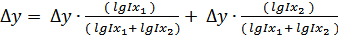В случае кратной модели для фактора, находящегося в знаменателе, коэффициент 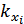берется со знаком минус.
Интегральный метод позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т.к. в нем действует логарифмический закон перераспределения факторных нагрузок. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.
Можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе:
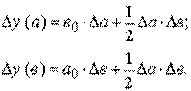1. Модель вида:
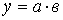
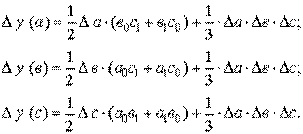2. Модель вида:
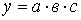
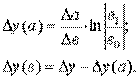3. Модель вида:
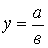
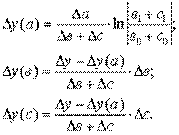4. Модель вида:
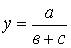
Контрольные вопросы:
1) Назовите основную задачу детерминированного факторного анализа.
2) Укажите основные этапы детерминированного факторного анализа.
3) Перечислите основные виды детерминированных моделей, используемых в факторном анализе.
4) Опишите алгоритмы применения основных способов детерминированного факторного анализа.
5) Какие приемы применяются для распределения неразложимого остатка по факторам?