Раздел 5. Основные понятия дискретной математики. Теория вероятности
Тема 5.2. Случайные величины
План
1. Случайные величины
2. Числовые характеристики случайных величин
3. Нормальный закон распределения. Закон больших чисел
1. Случайные величины
Опр. Случайной называют величину, которая принимает в результате испытания то или иное возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.
Дискретной называют такую случайную величину, которая принимает счётное множество значений, т.е. такое множество, элементы которого можно посчитать.
Непрерывной называют такую случайную величину, которая может принимать любые значения в определённом интервале.
Случайная величина считается заданной, если известен закон распределения случайной величины.
Опр. Распределением (законом распределения)случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими им вероятностями.
| Значение случайной величины хi | x1 | x2 | …… | xn |
| Вероятность значений pi | p1 | p2 | ……. | pn |
Табличную форму задания называют также рядом распределения.
Пример 4.1.
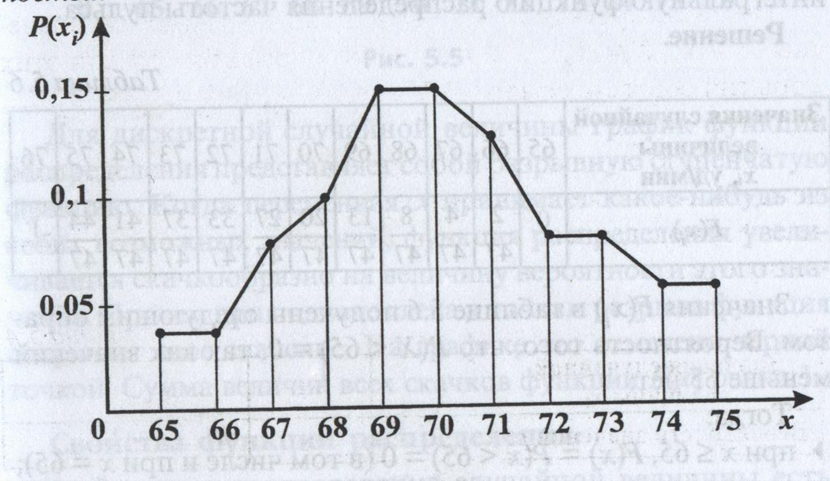
Построить график ряда распределения значений частоты пульса в гипотетической группе из 47 человек.
| Значение случайной величины уд/мин | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| Значения вероятности p (хi) |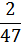 
|
| 
| 
| 
|
| 
|
|
| 
|
|
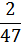
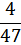
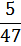
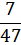
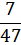
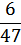
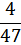
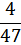
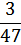
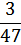
По данным таблицы построен график, который называется многоугольником распределения вероятностей.
Опр. Функция распределения определяет вероятность того, что случайная величина Х принимает значение, меньшее фиксированного действительного числа х, т.е.
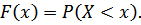
Функцию распределения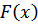 
иногда называют интегральной функцией распределения или интегральным законом распределения.
Свойства функции распределения:
1. Функция распределения случайной величины есть неотрицательная функция, заключённая между нулём и единицей: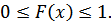 
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, и для любых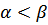 
выполняется равенство: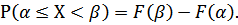 
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности – единице, т.е.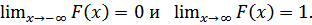 
Опр. Функцию f(x) называют дифференциальной функцией распределения, или плотностью распределения (плотностью вероятности), непрерывной случайной величины Х.
Основные свойства функции распределения:
1. Для любых х дифференциальная функция распределения неотрицательна, т.е.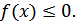 
2. Для дифференциальной функции распределения имеет место равенство: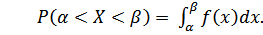 
3. Для дифференциальной функции распределения имеет место равенство: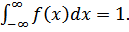 
Это свойство называется условием нормировки плотности вероятностей.
2. Числовые характеристики случайных величин
Математическое ожидание характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.
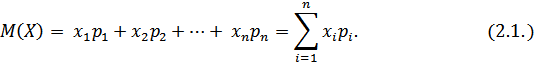
Для непрерывных случайных величин с плотностью распределения f(x) математическое ожидание равно определённому интегралу: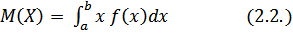 
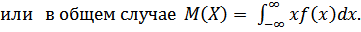(2.3.)
Пример 4.2.
Найти математическое ожидание дискретной случайной величины Х, зная закон её распределения.
| Х | -1 | 0 | 1 | 2 | 3 |
| р | 0,05 | 0,2 | 0,4 | 0,3 | 0,05 |
По формуле 2.1. (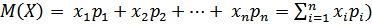 
находим:
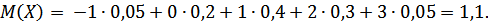
Пример 4.3.
Найти математическое ожидание непрерывной случайной величины Х, зная закон её распределения.
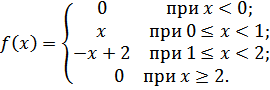
По формуле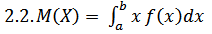 
находим:
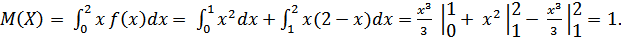
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно этой постоянной: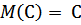 
.
2. Постоянный множитель можно выносить за знак математического ожидания: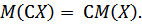 
3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий: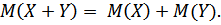 
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: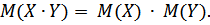 
5. Математическое ожидание отклонения случайной величины от её математического ожидания всегда равно нулю: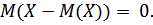 
Дисперсия характеризует рассеяние (отклонение) случайной величины относительно математического ожидания.
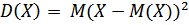. (2.4.)
Для дисперсии случайной величины: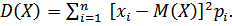 
(2.5.)
Для непрерывных случайных величин с плотностью вероятности f(x):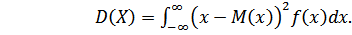 
(2.6.)
Размерность дисперсии равна квадрату случайной величины и её неудобно использовать для характеристики разброса, поэтому удобнее применять корень квадратный из дисперсии - среднее квадратическое отклонение. Эта величина даёт представление о размахе колебаний случайной величины около математического ожидания.
𝛿 (сигма)= √(𝐷(𝑋)).
Пример 4.4.
Случайная величина задана следующим рядом распределений.
| Х | -1 | 0 | 1 | 2 |
| р | 0,1 | 0,3 | 0,4 | 0,2 |
Найти математическое ожидание и дисперсию этой величины.
Для нахождения математического ожидания воспользуемся формулой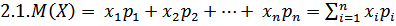 
, а для дисперсии 2.5. 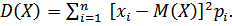Результаты вычисления сведём в таблицу.
| x | pi | xipi | xi - M(X) | (xi - M(X))2 | (xi - M(X))2 pi |
| -1 0 1 2 | 0,1 0,3 0,4 0,2 | -0,1 0 0,4 0,4 | -1,7 -0,7 0,3 1,3 | 2,89 0,49 0,09 1,69 | 0,289 0,147 0,036 0,338 |
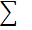
| 1 | 0,7 | 0,81 |
Из таблицы следует, что М(Х)=0,7; D(X)=0,81.
Пример 4.5.
Случайная величина задана плотностью вероятности:
Найти математическое ожидание и дисперсию этой величины.
По формуле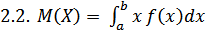 
находим:
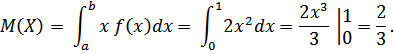
Далее по формуле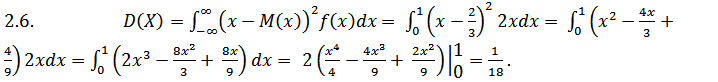 
Основные свойства дисперсии:
1. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X±Y)= D(X) ± D(Y).
2. Дисперсия постоянной величины С равна нулю: D(C) = 0.
3. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СX)= С2 D(X).
4. Дисперсия случайной величины Х равна разности между математическим ожиданием квадрата случайной величины и квадратом её математического ожидания: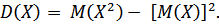 
3. Нормальный закон распределения. Закон больших чисел
Опр. Непрерывная случайная величина Х имеет нормальное распределение вероятностей с параметрами a и δ, если её плотность распределения задаётся формулой: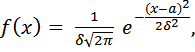 
Где а – математическое ожидание случайной величины; δ2 – дисперсия случайной величины; δ – среднее квадратическое отклонение.
Основные свойства распределения
1. Областью определения функции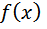 
является вся числовая ось.
2. Функция f(x) может принимать только положительные значения,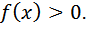 
3. Предел функции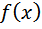 
при неограниченном возрастании 
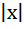равен нулю, т.е. Ох является горизонтальной асимптотой графика функции.
4. Функция 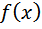имеет в точке х=а максимум, равный 
.
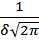5. График функции 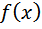симметричен относительно прямой х=а.
6. Кривая нормального распределения в точках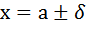 
имеет перегиб.
Закон больших чисел
Под законом больших чисел понимают совокупность теорем, в которых доказывается факт приближения средних характеристик к некоторым постоянным величинам в результате большого количества испытаний.
Теорема Чебышева
При неограниченном возрастании числа независимых, имеющих конечную дисперсию и проводимых в одинаковых условиях опытов, средняя арифметическая наблюдаемых значений случайной величины сходится по вероятности к её математическому ожиданию.