Лекция № 1. Множества. Действия с множествами. Действительные числа.
Понятие множества является первичным и не имеет чёткого математического определения. Однако под термином «множество» мы будем понимать любую совокупность определённых и различимых объектов, воспринимаемую как единое целое. Например, множество студентов, обучающихся в одном университете, множество капель в океане, множество чисел, множество точек на плоскости. Объекты, входящие в данное конкретное множество, называются его элементами. Различают конечные и бесконечные множества. Так, алфавит русского языка является конечным множеством, состоящим из 33 элементов, а множество всех молекул, составляющих атмосферу Земли, является бесконечным.
Множества обозначаются прописными латинскими буквами (A, B, C, D, …), а их элементы – строчными (a, b, c, d, …). Если объект a является элементом множества A, то пишут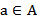 
. Запись 
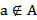означает, что элемент a не принадлежит множеству A. Если множество конечно, то элементы множества записываются в фигурных скобках: 
.
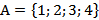Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В. Другими словами, множество А содержится в множестве В –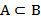 
, или множество В содержит множество А – 
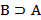(рис. 1).
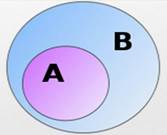
Рис. 1. Множество А содержится в множестве В
Множество, не содержащее ни одного элемента называется пустустым множеством и обозначается символом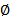 
. Любое множество содержит пустое множество в качестве подмножества.
Два множества A и B назваются равными, если они состоят из одних и тех же элементов.
Пример. Пусть даны два множества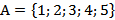 
и
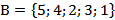. Эти множества состоят из одних и тех же элементов, поэтому 
.
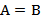Из примера ясно, что порядок элементов в множестве не существенен.
Объединением или суммой множеств A и B, называется множество, состоящее из элементов, принадлежащих или множеству A, или множеству B, и обозначается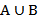 
(рис. 2, а).
Пример. Пусть даны два множества 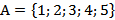и
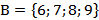, тогда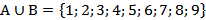 
Объединение двух множеств обладает коммутативным (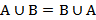 
) и ассоциативыным ( 
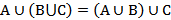) свойствами.
Пересечением множеств A и B, называется множество, состоящее из элементов, принадлежащих и множеству A, и множеству B, и обозначается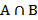 
(рис. 2, б).
Пример. Пусть даны два множества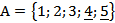 
и
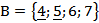, тогда 
.
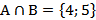Пересечение двух множеств, как и объединение, коммутативно (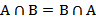 
) и ассоциативно ( 
).
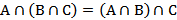Разностью множеств A и B, называется множество всех элементов множества A, не принадлежащих множеству B, и обозначается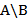 
(рис. 2, в).
Пример. Пусть даны два множества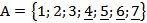 
и
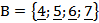, тогда 
.
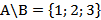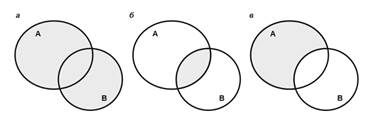
Рисунок 2. Операции над множествами:
объединение (а), пересечение (б), разность (в).
Множества, элементами которых являются числа, называются числовыми множествами. Рассмотрим примеры таких множеств:
‒ множество натуральных чисел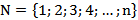 
;
‒ множество целых неотрицательных чисел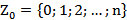 
;
‒ множество целых чисел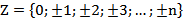 
;
‒ множество рациональных чисел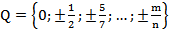 
;
‒ множество иррациональных чисел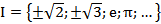 
;
Все эти множества являются подмножествами множества действительных чисел R. Множество действительных чисел является упорядоченным, плотным, непрерывным, бесконечным.
Упорядоченность множества действительных чисел заключается в том, что для любых действительных чисел a и b выполняется неравенство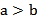 
или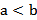 
.
Таблица 1.
| Обозначение | Неравенство | Изображение | |
| Отрезок | 
| 
| 
|
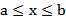
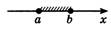
| Интервал |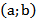 
| 
| 
|
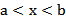
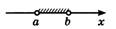
| Полуинтервал |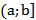 
| 
| 
|
| 
| 
| |
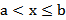
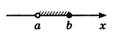
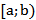
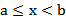
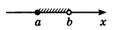
| Открытый луч |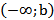 
| 
| 
|
| 
| 
| |
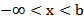
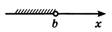
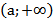
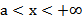
| Замкнутый луч |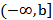 
| 
| 
|
| 
| 
| |
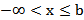
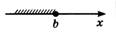
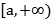
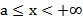
| Числовая прямая |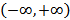 
| 
| 
|
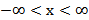
Между любыми двумя числами a и b содержится бесконечное множество чисел х, удовлетворяющих неравенству 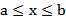. Это доказывает свойство плотности множества действительных чисел.
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством действительных чисел и множеством точек на прямой. Каждому числу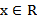 
соответствует единственная точка числовой оси, и наоборот, каждой точке прямой соответствует определенное действительное число.
Пусть a и b – действительные числа, причём 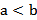. Множество действительных чисел, заключённых между этими числами, называется числовым промежутком. Числа a и b называются соответственно левым и правым концами рассмотренных промежутков. Символы 
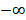и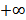 
не являются числами. Они обозначают процесс неограниченного удаления точек числовой оси от начала (нуля) влево или вправо. Основные виды числовых промежутков представлены в таблице 1.
Пусть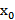 
– любое действительное число (точка на числовой оси). Окрестностью точки 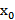называется любой интервал
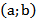, содержащий точку 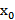(рис. 3а). В частности, интервал 
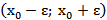, где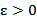 
, называется эпсилон-окрестностью точки 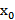(рис. 3б).
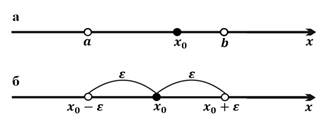
Рисунок 3. Окрестность точки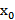
Число 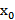– центр, 
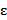– радиус эпсилон-окрестности. Если некоторое число 
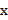принадлежит эпсилон-окрестности числа 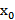, то выполняется неравенство 
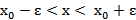или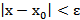 
.
Пусть 
– множество действительных чисел. Множество называется ограниченным сверху, если существует такое действительное число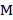 
, такое что для всех чисел 
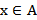выполняется условие 
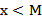. Аналогично, множество 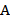называется ограниченным снизу, если существует такое действительное число 
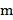, такое что для всех чисел 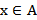выполняется условие 
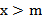. Множество 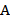называется ограниченным, если оно ограничено сверху и снизу.
Чтобы задать множесво, чаще всего используют два способа – перечисление всех его элементов и описание. При описании множества формулируется характеристическое свойство, которое устанавливает, принадлежит ему тот или иной элемент или нет.
Пример. Описать перечислением элементов множество
.
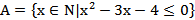Решение.
Данное множество описывается неравенством
.
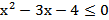Чтобы перечислить его элементы, найдём решение этого неравенства.
Составим и решим соответствующее квадратное уравнение
, 
;
;
;
.
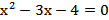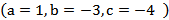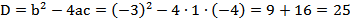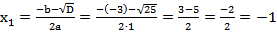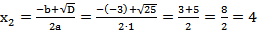Запишем формулу разложения квадратичного трёхчлена на множители:
.
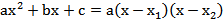В данном случае получим
.
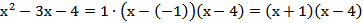Подставим полученное разложение в исходное неравенство
.
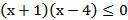Определим значения 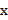, которые обращают левую часть неравенства в нуль:
;
.
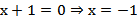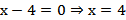Найденные значения разбивают числовую ось на три интервала. Изобразим нули квадратичного трёхчлена на числовой оси и определим его знаки на интервалах:
Рис.4
Из рисунка ясно, что неравенство верно на интервале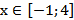 
. Так как, по условию задачи, 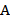– множество натуральных чисел, то
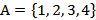. Таким образом, множество 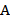задано путём перечисления его элементов.