Природа и структура расплавленных металлов
Лекция 2
КРИСТАЛЛИЗАЦИЯ ИЗ ЖИДКОЙ ФАЗЫ. ОБЩАЯ ТЕОРИЯ
ОБРАЗОВАНИЯ ФАЗ И КРИСТАЛЛИЗАЦИЯ
ОДНОФАЗНЫХ СПЛАВОВ
Природа и структура расплавленных металлов
Уже к концу 19 столетия и особенно за последние десятилетия в научной литературе накопились данные о таких фактах, которые заставили критически подойти к обычному противопоставлению жидкого состояния твердому и сближению его с газообразным. Прежде всего было установлено, что частицы соприкасающихся между собой твердых тел также способны «перемешиваться» путем диффузии, как и частицы двух жидкостей. Было открыто течение кристаллических тел при достаточно высоких температурах, происходящее под действием ничтожно малых сил.
Оказалось, что прочность твердых металлов при испытаниях на разрыв при температурах, близких к температуре плавления, совершенно ничтожна. С другой стороны, еще в 1911 г. удалось без разрыва растянуть жидкую ртуть на 1,4%, что отвечает отрицательному давлению около 100 кг/мм2, а вода была «растянута» на 1,5% (опыты велись в условиях, исключающих возможность течения жидкости).
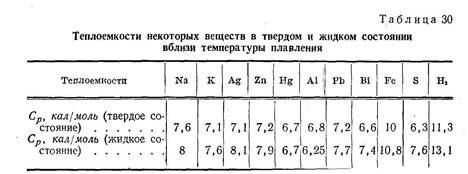
Было установлено, что теплоемкости веществ с простой кристаллической структурой лишь в незначительной степени меняются (обычно несколько возрастают) в результате плавления (табл. 30).Электрическое сопротивление большинства металлов при плавлении увеличивается примерно вдвое и при дальнейшем нагреве продолжает возрастать (у висмута, сурьмы, галлия плавление уменьшает электрическое сопротивление в полтора-два раза), металлическая природа вещества после плавления сохраняется.
Все это дает основание утверждать, что при плавлении характер сил взаимодействия между частицами не изменяется. Не изменяется существенно и величина сил взаимодействия, по крайней мере у металлов, поскольку теплоты плавления металлов не превышают 5—10% от теплот испарения. Как указал впервые Френкель, в жидкости, как и в твердом теле, частицы не движутся свободно, как в газе, а колеблются около положения равновесия. Только в отличие от твердых тел, в которых длительность пребывания частиц около положения равновесия в миллионы раз превышает периоды колебаний, в жидкостях частицы переходят в новые положения, совершив несколько тысяч колебаний около положения равновесия. Представление о наличии тепловых колебаний частиц в жидкости подтверждается как данными о теплоемкостях жидкостей, так и данными Е. Ф. Гросса о характере комбинационного рассеяния света прозрачными жидкостями, показывающими, что спектр тепловых колебаний в жидкости сходен со спектром тепловых колебаний в соответствующих кристаллах.
В последние десятилетия пришлось отказаться даже от представления о вполне аморфной структуре жидкостей, по крайней мере вблизи температуры плавления.
Многочисленные исследования показали, что диффракционная картина, получающаяся в результате рассеяния рентгеновых лучей жидкостями вблизи температуры плавления, во многом сходна с диффракционной картиной, характерной для рассеяния рентгеновых лучей теми же веществами в кристаллическом состоянии, существенно отличаясь от картины, которую дают пары тех же веществ.
Диффракционные максимумы рентгенограммы пара получаются в результате взаимодействия лучей, рассеянных атомами, принадлежащими одной и той же молекуле; углы рассеяния, им соответствующие, и характеризуют междуатомные расстояния в молекуле. Диффракционная картина для жидкостей гораздо богаче: здесь максимумы обусловлены наличием определенного порядка во взаимном расположении молекул (или атомов — в жидкостях атомарной структуры). Дебай и др. развили теорию рассеяния рентгеновых лучей жидкостями, молекулы которых обладают сферической симметрией. Формулы этой теории позволяют количественно описывать «порядок» в размещении молекул жидкости, если известна диффракционная картина рассеяния этой жидкостью монохроматических рентгеновых лучей.
В качестве характеристики «порядка» в расположении частиц жидкости принимается функция атомного размещения, определяемая из соотношения:
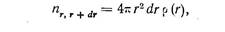(123)
где r — расстояние от центра какого-либо фиксированного атома;
пг,, r + dr — число центров атомов, находящихся в шаровом слое между сферами с радиусами r и r + dr , описанными вокруг этого атома.
Очевидно, r(r) представляет плотность жидкости на расстоянии r от центра фиксированного атома, выраженную в числах атомов на единицу объема.
На достаточно большом расстоянии от центра атома величина r(r) должна стремиться к постоянному значению, совпадающему со средней плотностью жидкостей rо.
Дебай характеризует расположение частиц с помощью функции вероятности w ( r ), представляющей отношение r(r) /rо.
Уравнения теории диффракции рентгеновых лучей позволяют вычислить функцию атомного размещения, если экспериментально получена кривая интенсивности рассеяния рентгеновых лучей в функции угла рассеяния J (обычно для удобства расчета кривые эти строятся так, что по оси абсцисс откладывается величина 2 sin J/2).
В идеальном кристалле при отсутствии теплового движения функция атомного размещения должна носить дискретный характер: все атомы кристалла должны находиться на некоторых определенных расстояниях от одного, центр которого принят за начало координат. Так, например, в идеальной простой кубической решетке расстояния rn 1 , n 2, n 3 любого атома Pn 1 , n 2, n 3 от атома, фиксированного в начале координат, выразится, очевидно, так:
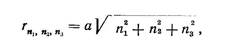
где а — период кристаллической решетки, равный в этом случае атомному диаметру, а — 2r0;
п1, п2, п3э-—три целых числа; каждое из этих чисел равно числу трансляций вдоль соответствующей кристаллографической оси, необходимому для перехода к данному атому Р п1,п2,п3 от начального атома Pо.
Очевидно, на одном и том же расстоянии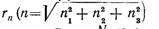 
от начального атома находятся несколько атомов, число N которых может быть определено путем перестановок п1, п2, п3э и замены этих величин отрицательными.
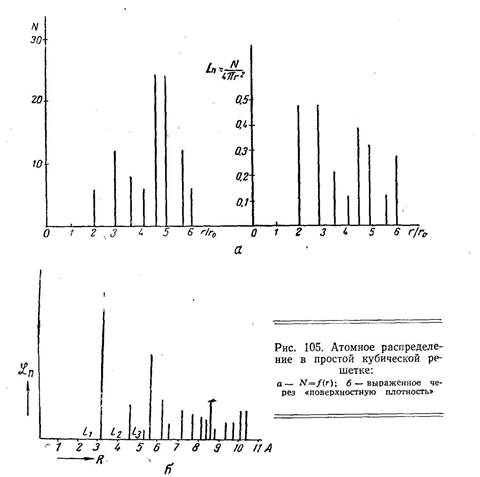
На рис. 105, а приведен график атомного распределения для идеальной простой кубической решетки, причем на оси ординат отложено число атомов N , центры которых находятся на расстоянии r от центра начального атома: 6 атомов находятся на расстоянии r 1 = 2 r 0 , 12 — на расстоянии r2 = 2,83 r 0 и т. д. Центры всех атомов располагаются на поверхностях дискретного ряда концентрических сфер с радиусами r1, r2 и т. д.
Для характеристики размещения атомов в идеальной решетке вводят «поверхностную плотность» Ln равную числу атомов, центры которых лежат на единице поверхности сферы радиусом rn т. е. Ln = Nn /4prn 2 .
Рис. 105, б характеризует поверхностную плотность для идеальной простой кубической решетки (за единицу измерения длины принят атомный радиус r 0, длины вертикальных прямых дают значения Ln ).
Тепловое движение в кристалле изменяет, размещение атомов — их центры отклоняются от идеальных положений на соответствующих сферах.
Вероятность нахождения атома вне соответствующей сферы оказывается отличной от нуля, она плавно спадает по обе стороны от rn, для которого вероятность максимальна, причем форма кривых размещения для всех rn одна и та же: вероятность определенного изменения расстояния Dr одна и та же для всех значений п.
Если принять, например, простейшее (на самом деле неточное) предположение о том, что вероятность нахождения атома линейно спадает по мере удаления от основной сферы, то прямые линии рис. 105 нужно будет заменить треугольниками с одинаковыми основаниями (рис. 106).
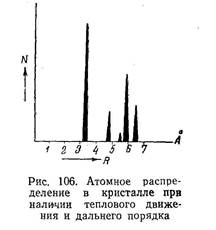
Такое размещение атомов характеризует наличие «дальнего порядка» в решетке. Средние смещения атомов по отношению к сфере, в которой они располагались бы в отсутствии тепловых колебаний, не зависят при наличии дальнего порядка от числа п.
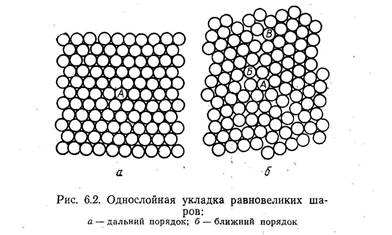
Анализ кривых рассеяния рентгеновых лучей жидкостями привел к представлению о том, что в жидкости сохраняется лишь «ближний» порядок расположения частиц.
Ближний порядок характеризуется тем, что средние смещения атомов по отношению к идеальным сферам растут с увеличением п; относительное смещение двух далеко расположенных атомов А и В оказывается при наличии одного лишь ближнего порядка векторной суммой взаимных смещений "промежуточных атомов. Применение к этому статистическому суммированию идей, лежащих в основе теории броуновского движения, приводит к выводу, что смещение это пропорционально квадратному корню из расстояния между атомами А и В. Различие в распределении атомов при ближнем и дальнем порядке иллюстрируется рис. 106 и 107.
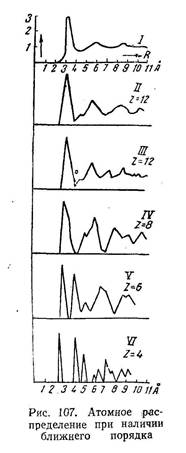
Представление о «ближнем порядке» связано с представлением об исходной идеальной структуре, которая «размывается» при плавлении. На рис. 107, II - VI , показаны функции атомной плотности, построенные при некоторых упрощающих предположениях для ближнего порядка при исходных решетках компактной гексагональной (// — координационное число z =12), кубической гранецентрированной (/// — z =12), объемноцентрированнной ( IV — z = 8), простой ( V — z = 6), а также для решетки с тетраэдрической координацией ( VI — z = 4). Расчеты проведены для ртути, междуатомные расстояния 2г0 в исходной решетке вычислены из плотности жидкого металла. График I того же рисунка изображает функцию вероятности для жидкой ртути, построенную на основании кривой рассеяния рентгеновых лучей. Эта кривая весьма сходна с линией, построенной теоретически для «размытой» компактной гексагональной решетки. Площадь кривой под первым максимумом определяет среднее число ближайших соседей у каждого атома жидкости, местоположение первого максимума — среднее расстояние между соседними атомами.
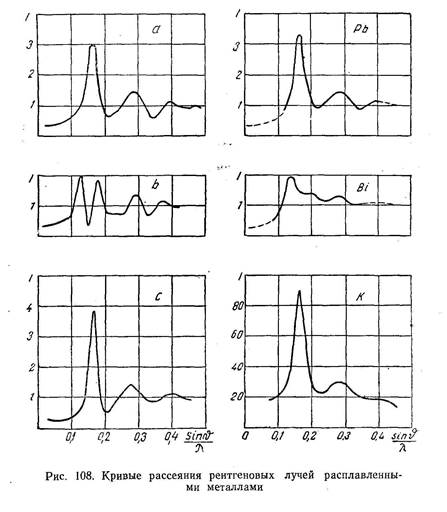
На рис. 108 представлены полученные А. И. Даниловой экспериментально кривые рассеяния жидким калием, свинцом и висмутом и сопоставление с кривыми, вычисленными для размытых кубических решеток.
Как указывают авторы, бросается в глаза большое сходство кривой для лучей, рассеянных расплавленным свинцом, с теоретической кривой а (рис. 108), построенной для гранецентрированной решетки (для калия) с кривой с (объемноцентрированная решетка), для висмута — с кривой b (простая решетка). Во всех рассмотренных здесь случаях взаимное расположение атомов, характерное для «ближнего порядка» в расплавленных металлах вблизи точки плавления, аналогично взаимному расположению атомов в кристаллах соответствующих металлов (следует иметь в виду, что ромбоэдрическая решетка кристаллического висмута очень сходна с простой кубической решеткой, так что отличить их друг от друга по нечеткой рентгенограмме расплава невозможно).
На рис. 109 дана кривая атомного размещения, построенная А. И. Даниловой, В. И. Даниловым и Е. 3. Спектор, для расплавленного висмута по кривой рассеяния рентгеновых лучей. На этом же графике приведена кривая 4pr2ro(I), построенная для равномерного распределения атомов с постоянной средней плотностью ro. Вертикальные линии дают атомное распределение для кристаллического висмута i.
В кристаллическом висмуте у каждого атома имеется 6 соседей: три — на расстоянии 3,09 Å и три — на почти таком же расстоянии в 3,46 Å. Его структура чрезвычайно сильно отличается от плотноупакованной с 12 соседями у каждого атома. В расплавленном висмуте среднее расстояние между ближайшими соседями, как видно из рис. 109, равно 3,25 Å, что очень близко к среднему значению для решетки висмута
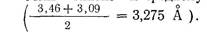Число ближайших соседей у атома в расплавленном висмуте, как показало измерение площади под первым максимумом, равно 7—- 7,5 вместо 6 у кристаллического висмута. Таким образом, плавление висмута, имеющего не плотно упакованную решетку, вызывает вместе с общим «размытием» структуры и некоторое изменение упаковки атомов, направленное в сторону повышения «плотности» упаковки. Это обстоятельство является причиной уменьшения удельного объема висмута при плавлении.
Как видно из графика рис. 109, по мере увеличения расстояния r от начального атома вычисленная по экспериментальным данным кривая все меньше отличается от кривой,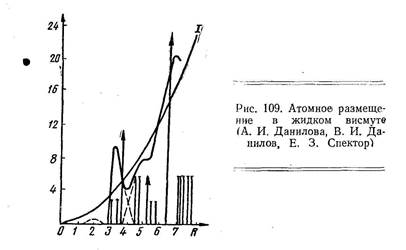 
построенной для равномерного распределения, порядок ощущается все слабее, поэтому-то он и называется ближним.
С повышением температуры расплавленного металла интерференционные максимумы на кривой рассеяния размываются, что свидетельствует об увеличении размытия структуры.
В. И. Данилов указывает, что разного типа идеальные решетки размываются при плавлении в разной степени: всего четче сохраняется ближний порядок после расплавления металлов с компактными решетками (гексагональной и гранецентрированной кубической, например, ртуть, свинец), гораздо сильнее сглаживаются интерференционные максимумы на кривых рассеяния расплавленных металлов с рыхлыми «идеальными» упаковками, характеризующимися малыми координационными числами (висмут, калий).
Резкое ослабление ближнего порядка после плавления металлов с рыхлыми упаковками объясняется тем, что тепловое движение частиц стремится сделать размещение атомов наиболее компактным, т. е. стремится увеличить координацию атомов. На ближний порядок в расплавленных металлах с компактными идеальными решетками эта тенденция теплового движения, очевидно, не влияет, поэтому-то в таких металлах идеальная решетка размывается после плавления гораздо слабее.
В. И. Данилов и М. А. Левашевич показали, что разные органические вещества ведут себя при плавлении по-разному. Кривая рассеяния для некоторых из них (например, для ортохлорнитробензола) в жидком состоянии имеет, как и в случае металлов, те же интерференционные максимумы, что и рентгенограмма поликристаллического твердого вещества. Идеальная решетка таких расплавов совпадает с кристаллической решеткой тех же веществ в твердом состоянии. Но многие органические вещества (например, салол, бензофенон, салипирин) изменяют при плавлении идеальную решетку.
При изучении структуры воды Бернал и Фаулер установили, что разным температурам отвечают три разные формы взаимного расположения молекул. В воде I расположение это аналогично весьма рыхлому размещению молекул кремнекислоты в кристаллах тридимита, высокотемпературной модификации SiO2 (ту же структуру имеет лед вблизи температуры таяния); незначительное количество воды I содержится в воде при температурах от 0 до 4° С, постепенная замена воды I более компактной водой II (структура a-кварца) обусловливает аномальное сжатие воды при нагреве до 4°. При более высоких температурах делается заметной вода III с наиболее компактным размещением молекул. Вода III преобладает при температурах, близких к критической. Исследуя рассеяние рентгеновых лучей в расплавленных металлических эвтектиках Pb-Bi, Pb-Sn, Bi-Sn В. И. Данилов и И. В. Радченко показали, что интерференционные картины, наблюдающиеся при этом, могут быть истолкованы, как результат наложения интерференционных картин, характерных для расплавов компонентов, входящих в эти эвтектики (см., например, на рис. 110, .а и б кривую рассеяния, полученную экспериментально для жидкой эвтектики Pb-Bi, с линией, найденной путем суммирования кривых для чистых РЬ и Bi).
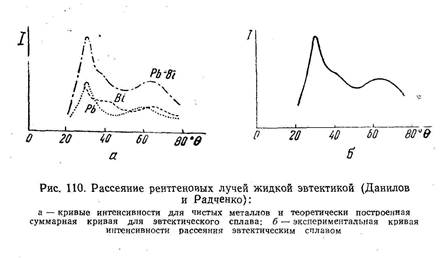
Авторы делают отсюда заключение о том, что в каждом из изученных ими двойных эвтектических сплавов имеются области, ближний порядок в которых отвечает кристаллической структуре компонента A, и области с ближним порядком, характерным для компонента В. Несомненно области эти непрерывным образом переходят друг в друга и ни в какой мере не являются стабильными благодаря идущему непрерывно перемешиванию, обусловленному тепловым движением. По мнению Данилова, в областях с ближним порядком компонента А преобладают атомы А, в областях с ближним порядком компонента В — атомы В. К. П. Бунин, подвергая центрифугированию расплавленную эвтектику Bi-Sn и анализируя распределение компонентов по закристаллизовавшемуся в процессе центрифугирования слитку, также приходит к заключению о существовании в жидкой эвтектике областей, содержащих преимущественно атомы одного из компонентов, и областей, состоящих главным образом из атомов второго компонента. Расчеты, которых мы здесь не приводим, позволяют Бунину заключить, что размеры этих областей — величины порядка 50 элементарных ячеек.
При изучении рассеяния поляризованного света в жидкостях было сделано заключение о существовании в некоторых жидких прозрачных эвтектиках обособленных областей, содержащих преимущественно молекулы одного или другого компонента. По расчетам размеры этих областей достигают величин того же порядка, что и длины волн видимого света (т. е. несколько десятых долей микрона). Качественное теоретическое объяснение причин такого «эмульсоидного» состояния жидких эвтектик, основанное на учении о поверхностных явлениях, Я. И. Френкель.
Расположение максимумов на кривых рассеяния расплавленными интерметаллическими соединениями Hg5Tl2, Hg2K существенно отличается от интерференционных картин для чистых компонентов. Можно предполагать, что эти расплавы являются жидкими аналогами соответствующих кристаллических интерметаллических фаз.
Имеется большое количество работ, в которых также показано сходство кривых рассеяния разнообразными неметаллическими (преимущественно органическими) жидкостями с интерференционной картиной, получаемой при рассеянии рентгеновых лучей теми же веществами в твердом состоянии.
Одно время было широко распространено особое толкование кривых рассеяния рентгеновых лучей жидкостями. Обращали внимание на то, что такие же интерференционные картины получились бы, если бы жидкости состояли из мельчайших (с линейными размерами порядка 10-6—10-7 см) образований, внутри которых господствовал не только ближний, но и дальний порядок. Такие гипотетические образования были названы «сиботаксическими группами». Считали, что сиботаксические группы, в отличие от кристалликов, которые могут плавать в жидкой фазе, не имеют явно выраженных поверхностей, отделяющих их от массы окружающего вещества, и плавно переходят друг в друга. Сиботаксические группы неустойчивы: в результате теплового движения они возникают и разрушаются, просуществовав ничтожно малое время.
Поскольку термодинамическое объяснение возможности существования сиботаксических групп до сих пор не найдено, В. И. Данилов считает целесообразным не пользоваться этим понятием и ограничиваться представлениями о ближнем порядке и о «размытой» решетке в жидкостях.