Рис. 8.2. Возможности реализации комбинационных схем
Лекция 8
8. Комбинационные логические схемы
………………….. Прочитано
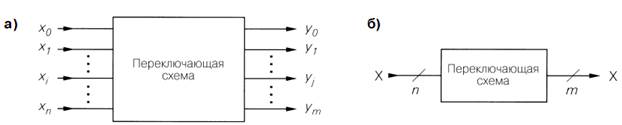
Рис. 8.1. Диаграмма комбинационной схемы:
а – прохождение сигналов; б – прохождение векторов
………………….. Прочитано
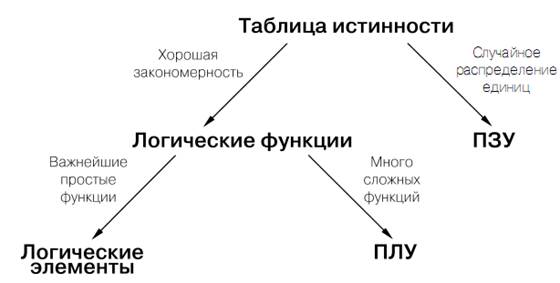
Рис. 8.2. Возможности реализации комбинационных схем
………………….. Прочитано
Обычно комбинационные схемы применяются для пересчета и перекодирования чисел. Чтобы иметь возможность представлять числа посредством логических
переменных, сами числа должны отображаться в виде последовательности двоичных чисел, то есть способных принимать только два значения. Двоичную цифру называют битом. Существует особая двоичная форма представления чисел с помощью двоичных знаков (двоичная система счисления), в которой разряды числа упорядочены по возрастающей степени числа 2. При этом цифра 1 отождествляется с логической единицей, а цифра 0 – с логическим нулем. Будем обозначать строчными буквами логическую переменную, характеризующую отдельное знакоместо в числе, а прописными буквами – все число. Тогда для представления числа из N разрядов в двоичном виде можно записать:
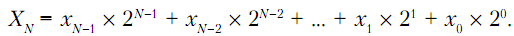(8.1)
Разумеется, следует всегда четко разграничивать вычислительные операции с числами и составление функций из логических переменных. Еще раз поясним это различие на примере. Рассчитаем выражение 1 + 1. Полагая, что знак (+) обозначает сложение в десятичной системе счисления, получим соотношение:
1 + 1 = 2.
Сложение в двоичной системе дает
1 + 1 = 102
(читается: «единица–нуль»).
8.1. Представление чисел
Цифровые схемы способны обрабатывать только двоичные данные, поэтому приходится переводить числа из привычной десятичной системы счисления в двоичную. Для этого есть разные возможности, о чем и пойдет речь в следующих разделах.
8.1.1. Положительные целые числа в двоичном коде
Самым простым средством представления двоичных чисел служит двоичный код.
Разряды упорядочены по возрастанию степени числа 2. Для обозначения числа из N разрядов в двоичном коде справедлива запись:
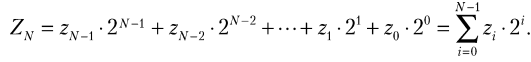(8.2)
В соответствии с десятичной системой просто записывают последовательность
цифр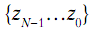 
и мысленно складывают соответствующие степени числа 2.
Пример 8.1
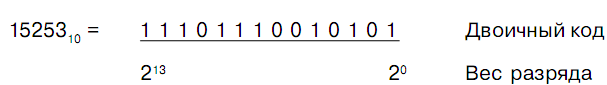
Восьмеричный код
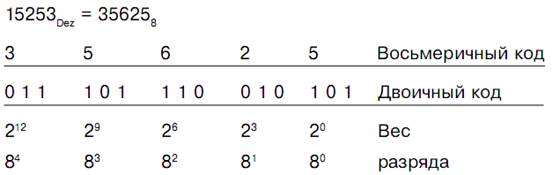
Очевидно, двоичный код воспринимается с трудом. Поэтому пользуются сокращенной формой записи, при которой каждые три разряда двоичного кода сводятся к одной цифре, а значение такого 3-разрядного двоичного числа записывается в десятичном виде. Поскольку соответствующие числа упорядочены по возрастанию степеней 23 = 8, такой код называют восьмеричным.
Пример 8. 2
Шестнадцатеричный код
Еще один распространенный способ сокращенной записи состоит в том, чтобы сводить к одному числу по четыре двоичных разряда. В таком случае возникающие числа упорядочиваются по возрастанию степени числа 24 = 16, в силу чего код получил название шестнадцатеричного. В каждом разряде числа могут принимать значения от 0 до 15, но для этого десятичных цифр уже недостаточно, и потому цифры от 10 до 15 отображаются символами от A до F.
Пример 8. 3
8.1.2. Положительные целые числа в двоично-десятичном коде
Ввод и вывод чисел в двоичной форме (т.е. операция, связанная с восприятием чисел человеком) неудобен, так как мы привыкли вести расчеты в десятичной системе. В итоге был создан двоично-десятичный код (ДДК), где каждая десятичная цифра представляется в виде двоичного числа.
Пример 8. 4
Число, записанное в таком виде, правильнее называть двоично-десятичным
числом в коде 8421 или натуральным двоично-десятичным числом. Отдельные
десятичные цифры могут быть представлены четырьмя двоичными разрядами, но
поскольку код 8421 получил наибольшее распространение, его часто именуют просто двоично-десятичным кодом.
4-разрядное двоичное число позволяет отображать десятичные числа от 0 до 15.
В ДДК из них используется только 10 комбинаций, поэтому для представления одного и того же числа в ДДК требуется больше битов, чем в двоичном коде.
8.1.3. Целые двоичные числа с произвольным знаком
Отрицательное число характеризуется тем, что перед старшим разрядом ставится
бит знака s.
Представление модуля и знака
Число положительно, если s = 0, и отрицательно, когда s = 1. Однозначная интерпретация возможна только при фиксированной длине двоичного слова.
Пример 8.5
Для слова длиной 8 бит:
8.2. Мультиплексор
Мультиплексором называют схему, которая подключает любой из множества источников данных к единственному выходу, причем выбор источника определяется
его адресом. Схема обратного действия называется демультиплексором. Он распределяет данные по множеству выходов в соответствии с принятой адресацией. Обе схемы основаны на адресации с применением дешифратора «один из n» (дешифратор со стробированием).
8.2.1. Дешифратор «один из n»
Дешифратор «один из n» представляет собой схему с n выходами и ln n входами.
Выходы yJ нумеруются от 0 до (n – 1). Сигнал на том или ином выходе принимает
значение логической единицы, когда двоичное число A на входе равно номеру J соответствующего выхода. Таблица истинности для дешифратора «1 из 4» приведена в табл. 8.4. Переменные a0 и a1 служат двоичным кодом числа A. Это позволяет непосредственно считывать дизъюнктивную нормальную форму функций перекодировки. Соответствующая реализация показана на рис. 8.5.
8.2.2. Демультиплексор
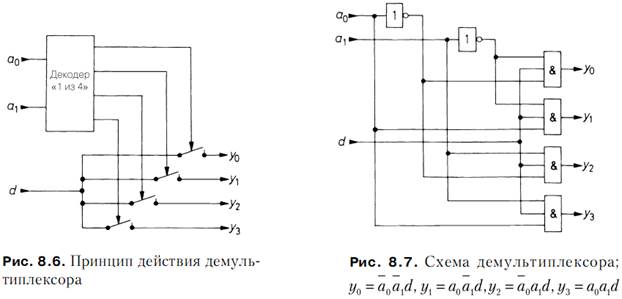
Демультиплексор позволяет направлять входную информацию d на различные выходы и представляет собой расширение дешифратора «один из n». Адресуемому
выходу присваивается не единица, а значение входной переменной d. На рис. 8.6
показан принцип действия на примере схемы с ключами, а на рис. 8.7 демонстрируется реализация с помощью логических элементов. При d = const = 1 демультиплексор функционирует как дешифратор «один из n».
8.2.3. Мультиплексоры
Устройство с функциями, обратными демультиплексору, называется мультиплексором. Следуя принципу действия схемы, показанной на рис. 8.6, для реализации мультиплексора достаточно поменять местами выходы с входами. Результат такой замены показан на принципиальной схеме (рис. 8.8), доступно объясняющей функционирование мультиплексора: дешифратор «один из n» выбирает из n входов тот,
чей номер совпадает с заданным числом, и подключает его к выходу. Соответствующая реализация с помощью логических элементов показана на рис. 8.9.
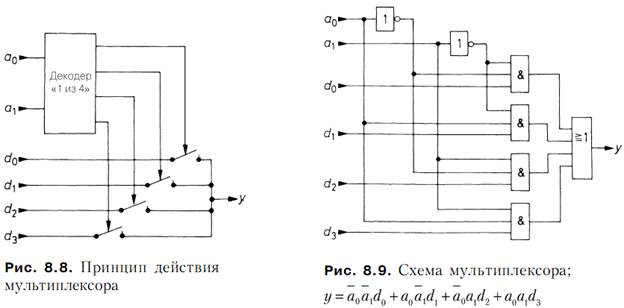
В КМОП технологии мультиплексоры реализуются как на логических элементах, так и на аналоговых ключах (передаточных вентилях). Последние обеспечивают двунаправленную передачу сигнала, так что мультиплексор и демультиплексор
становятся неразличимыми (ср. рис. 8.6 и 8.8). В этом случае схему называют аналоговым мультиплексором/демультиплексором.
Функция ИЛИ, необходимая в мультиплексорах, реализуется в виде «монтажного» ИЛИ. Данная возможность иллюстрируется на рис. 8.10 для случая, когда логические элементы обладают выходами с открытым коллектором. Поскольку в положительной логике при этом получается функция И, необходимо переходить к инвертированным сигналам.
Если желательно обойти недостаток, присущий выходам с открытым коллектором и проявляющийся в более длительном нарастании сигнала, следует воспользоваться параллельным включением выходов с тремя состояниями, активизируемых
по одному в каждый момент времени (рис. 8.11).
Возможности реализации функции ИЛИ, показанные на рис. 8.10 и 8.11, не применяются в интегральных мультиплексорах. Однако они важны там, где имеются
пространственно разнесенные источники сигналов для мультиплексора, например,
в системах с шинной организацией.
8.5. Компараторы
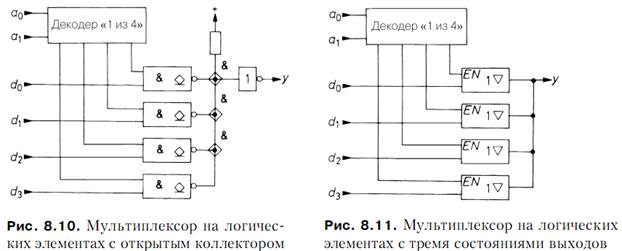
Компараторами называют схемы для сравнения двух чисел. Важнейшими критериями сравнения служат условия A = B, A > B и A < B. Прежде всего, нужны компараторы, способные установить равенство пары двоичных чисел. Критерием равенства двух чисел является поразрядное совпадение этих чисел. На выходе
компаратора должна появляться логическая единица при равенстве пары чисел и
логический нуль – в противном случае. В простейшей ситуации сравниваются одноразрядные числа. Тогда компаратором может служить логический элемент Исключающее ИЛИ–НЕ. Два N-разрядных числа сравнивают бит за битом с помощью схем Исключающее ИЛИ–НЕ, а их выходы объединяют логической схемой И (рис. 8.15).
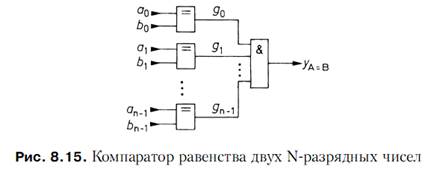
Компараторы, способные определять не только равенство чисел, но и находить
большее из них, считаются универсальными. Такие схемы называют компараторами по величине.
8.6. Сумматоры
Схемы для сложения двух чисел называются сумматорами. Вычитание может быть
сведено к сложению.
8.6.1. Полусумматоры
Сумматоры служат для сложения двух двоичных чисел. Сложение одноразрядных
чисел является простейшей задачей. Для построения логической схемы необходимо прежде всего исследовать все вероятные ситуации, что позволит составить таблицу истинности. При сложении пары одноразрядных чисел A и B возможны ниже перечисленные случаи:
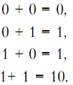(8.3)
Если A и B равны 1, результат сложения появляется и в следующем по старшинству разряде, поэтому сумматор должен иметь два выхода: один для составляющей суммы в данном разряде, а другой для переноса в следующий разряд. Для
построения таблицы истинности обозначим числа A и B логическими переменными a0 и b0. Компонент переноса обозначается переменной c1, а сумма – переменной s0.
Составив дизъюнктивную нормальную форму, получим булевы функции:
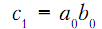(8.4)
и
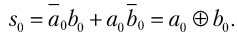(8.5)
Таким образом, сигнал переноса реализуется логической схемой И, а сумма –
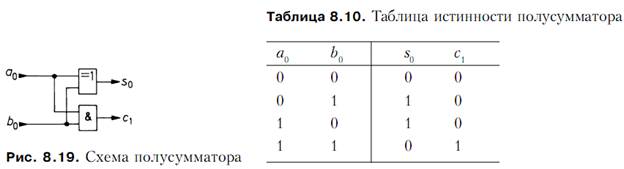
логической схемой Исключающее ИЛИ. Схема, реализующая обе функции, называется полусумматором (рис. 8.19). Таблица истинности полусумматора приведена
в табл. 8.10.
8.6.2. Полный сумматор
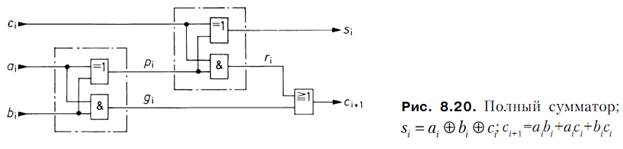
При сложении многоразрядных двоичных чисел полусумматор справляется только с самыми младшими разрядами. Во всех остальных разрядах приходится складывать не два, а три бита, поскольку добавляется перенос из ближайшего низшего разряда. Таким образом, в общем случае для каждого бита требуется логическая схема с тремя входами ai, bi и ci и двумя выходами si и ci+1. Такую схему называют полным сумматором, реализуемым с помощью двух полусумматоров (рис. 8.20); таблица истинности полного сумматора представлена в табл. 8.11.
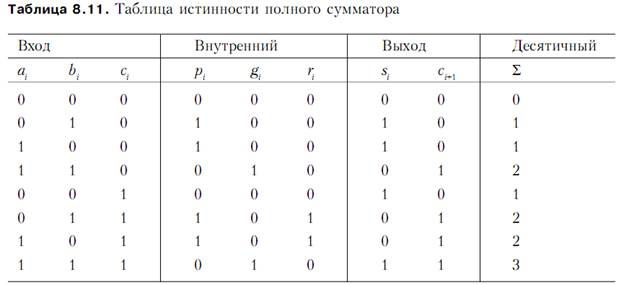
При сложении многоразрядных двоичных чисел на каждый разряд требуется
по одному полному сумматору. В самом младшем разряде достаточно полусумматора. На рис. 8.21 приведена схема для сложения пары 4-разрядных чисел A и B. Подобные схемы имеются в интегральном исполнении.
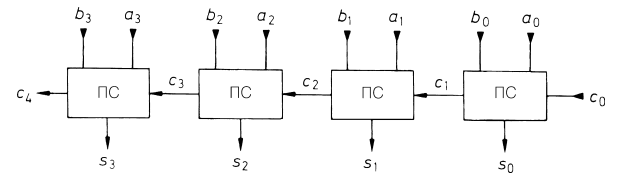
Рис. 8.21. 4-разрядное сложение с последовательным переносом
8.6.4. Вычитание
Вычитание двух чисел сводится к сложению, так как
(8.6)