Проекция вектора на ось
Пусть в пространстве задана ось l, то есть направленная прямая. Проекцией точки М на ось l, называется основание перпендикуляра М1, опущенного из точки М на ось.
 |
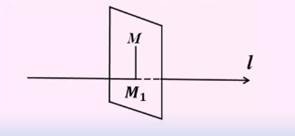Если точка М лежит на оси l, то проекция точки М на ось совпадает с М.
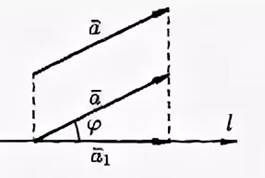
Пусть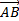 
– произвольный ненулевой вектор. Обозначим через А1 проекцию начала вектора, через В1 – проекцию конца вектора, тогда проекцией вектора 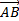на ось l называется отрезок А1В1 между проекцией начала вектора 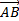и проекцией его конца.
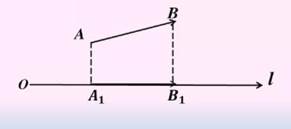
Если вектор 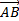и ось l одинаково направлены, то проекция А1В1 положительна; если вектор 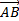и ось l противоположно направлены, то проекция А1В1 отрицательна. Если точки А1 и В1 совпадают, то проекция вектора 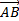равна нулю.
Проекция вектора 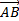на ось l обозначается в виде 
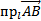. Если 
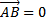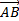или перпендикулярен оси l, то 
.
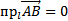Чтобы найти угол φ между вектором и осью (или между двумя векторами) нужно путём параллельного переноса совместить начало вектора 
с осью (или с началом другого вектора), тогда угол, отсчитанный от положительного направления оси (вектора) против часовой стрелки, и есть угол φ.
Свойства проекций
1. Проекция вектора 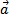на ось l равна произведению модуля вектора 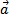на косинус угла φ между вектором и осью 
.
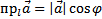Следствия:
‒ проекция вектора на ось положительна, если вектор образует с осью острый угол, и отрицательна, если вектор образует с осью тупой угол;
‒ проекции равных векторов на одну и ту же ось равны между собой.
2. Проекция суммы нескольких векторов на одну и ту же ось равна алгебраической сумме их проекций на эту ось.
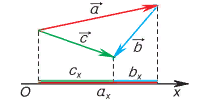
3. При умножении вектора 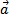на число λ его проекция также умножается на это число, то есть 
.
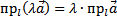Таким образом, линейные операции над векторами приводят к соответствующим операциям над проекциями этих векторов.
Разложение вектора по ортам координатных осей. Модуль вектора
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на осях Ox, Oy, Oz единичные векторы (орты), обозначаемые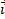 
, 
, 
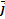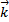соответственно. Выберем вектор 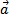в пространстве и совместим его начало с началом координат (рис.).
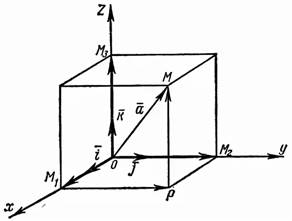
Из рисунка видно, что
, 
, 
.
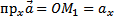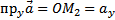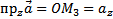По правилу параллелепипеда,
,
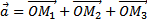где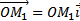 
, 
, 
.
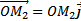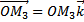Тогда
.
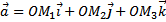Окончательно получим формулу разложения вектора по ортам координатных осей:
.
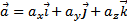Числа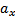 
, 
, 
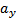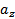называются координатами вектора. Другими словами, координаты вектора 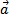есть его проекции на соответствующие координатные оси: 
.
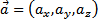Пусть 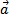и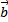 
два данных вектора. Если вектор 
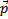представлен в виде 
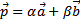, где α и β - некоторые числа, то говорят, что вектор 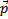разложен по векторам 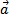и 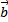. Числа α и β называются коэффициентами разложения.
Теорема. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Аналогично, если три вектора 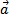, 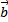и 
не компланарны, то любой вектор можно разложить по этим векторам
,
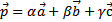причем коэффициенты разложения определяются единственным образом.
Зная координаты вектора, можно легко найти выражение для его модуля. По теореме о длине диагонали параллелепипеда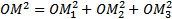 
, следовательно
.
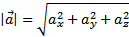Таким образом, модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Действия над векторами, заданными проекциями
Пусть векторы 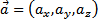и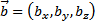 
заданы своими проекциями на оси координат Ox, Oy, Oz или, что то же самое, 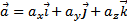и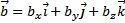 
.
Линейные операции над векторами
1. Сложение (вычитание). При сложении (вычитании) векторов их одноимённые координаты складываются (вычитаются):
.
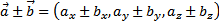2. Умножение вектора на число. При умножении вектора на число координаты вектора умножаются на это число:
.
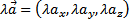Признак коллинеарности векторов
Если векторы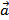 
и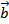 
коллинеарны, то 
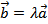, где λ – некоторое число. Отсюда
.
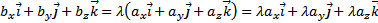Следовательно,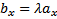 
, 
, 
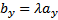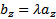, то есть 
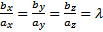. Проекции коллинеарных векторов пропорциональны и, наоборот, векторы, имеющие пропорциональные координаты, коллинеарны.
Координаты точки и вектора
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М вектор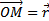 
называется радиус-вектором точки М (рис.).
Рис.
Следовательно, координаты точки – это координаты радиус вектора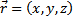 
или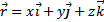 
. Координаты точки М записываются в виде М (x,y,z).
Найдём координаты вектора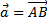 
, если известны координаты точек А(x1, y1, z1) и В (x2, y2, z2).
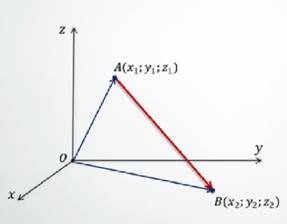
Имеем
.
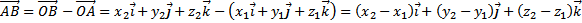Таким образом, чтобы найти координаты вектора, нужно из координат конца вычесть координаты начала: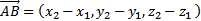 
.