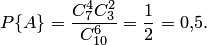Свойства вероятности
Свойство 1. Если все случаи являются благоприятствующими данному событию 
, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 
, так как в этом случае 
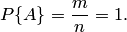
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 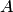, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 
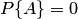, так как в этом случае 
:
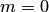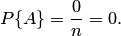
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 4. Вероятность наступления противоположного события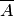 
определяется так же, как и вероятность наступления, события :
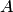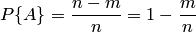
где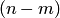 
— число случаев, благоприятствующих появлению противоположного события 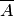. Отсюда вероятность наступления противоположного события 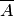равна разнице между единицей и вероятностью наступления события :
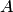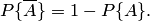
| (1.2) |
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим 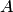событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию 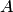лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
.
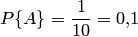Элементы комбинаторики
В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество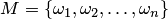 
, то размещением (сочетанием) из 
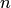элементов по 
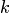называется любое упорядоченное (неупорядоченное) подмножество 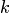элементов множества 
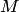. При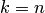 
размещение называется перестановкой из 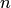элементов.
Пусть, например, дано множество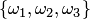 
. Размещениями из трех элементов этого множества по два являются 
, 
, 
, 
, 
, 
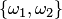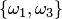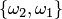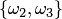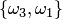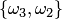; сочетаниями — , , .
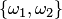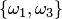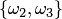Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из 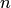элементов по 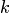вычисляется по формуле
,
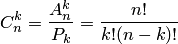где
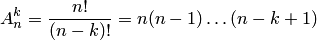
есть число размещений из 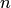элементов по ; 
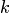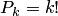— число перестановок из 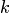элементов.
Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.
Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно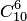 
— числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию 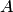(среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей 
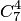способами; при этом остальные 
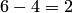детали должны быть нестандартными; взять же 2 нестандартные детали из 
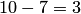нестандартных деталей можно 
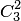способами. Следовательно, число благоприятствующих исходов равно 
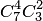. Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:
