Схема Бернулли. Формула Бернулли.
Пусть производится n независимых однотипных испытаний, в каждом из которых событие А может появиться с вероятностью Р. Тогда вероятность непоявления события А, т.е. Р( 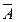 ) равна q=1-p.
) равна q=1-p.
Вероятность того, что событие А произойдет в этих n независимых испытаниях ровно k раз, можно вычислить по формуле Бернулли
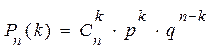
Для определения вероятности появления события A менее m раз (k < m), более m раз (k > m), хотя бы один раз ( 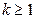 ) и т. п. могут быть использованы формулы:
) и т. п. могут быть использованы формулы:
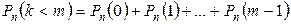 ,
,
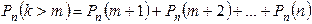 ,
,
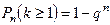 .
.
Пример : Прибор состоит из пяти узлов. Надежность (вероятность безотказной работы в течение времени t ) для каждого узла равна 0,9. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время t откажут ровно два узла.
Решение: Рассмотрим событие А - выход узла из строя за время t. Число узлов n=5. Число отказавших узлов за время t: k=2.
Р(А) - вероятность выхода узла из строя: p =P(A)=0,1. Тогда q=1-p=1-0,1=0,9.
Теперь вычислим искомую вероятность по формуле Бернулли:
Р5(2) = 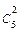 (0,1)2 .(0,9)3=10.0,01.0,729=0,0729.
(0,1)2 .(0,9)3=10.0,01.0,729=0,0729.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
1.1. Закон распределения дискретных случайных величин
1.2. Случайная величина (СВ) – это величина, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать, какое именно значение она примет.
(Более точно, СВ - это действительная функция, определенная на пространстве элементарных событий Ω).
Случайные величины обозначаются буквами латинского алфавита X, Y, Z.
Случайные величины могут быть трех типов:
· дискретные,
· непрерывные,
· смешанные (дискретно-непрерывные).
Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений.
Например, подбрасываем монету 5 раз. Случайная величина X- число появлений герба: 0,1,2,3,4,5.
Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений.
Например, мишень имеет форму круга радиуса R. По этой мишени произвели выстрел с обязательным попаданием. Обозначим через Y расстояние от центра до точки попадания в мишень, Y є [0; R].
Y – непрерывная случайная величина, так как она принимает бесконечное несчетное число значений.
Пусть X - дискретная случайная величина, которая принимает значения: x1, x2, ..., хn... с некоторой вероятностью pi ,где i = 1,2,..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение хi: pi = P(X = xi).
Значения хi, и соответствующие рi, представляют в виде таблицы:
| xi | x1 | x2 | x3 | … | xn | … |
| pi | p1 | p2 | p3 | … | pn | … |
Эта таблица является одной из форм задания ДСВ. Обычно случайные величины располагаются в возрастающем порядке. Основное свойство таблицы заключено в том, что сумма вероятностей равна 1:
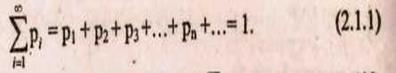
Пример 1.1. Монета бросается 5 раз. Представим закон распределения ДСВ Х- числа появлений герба, в виде таблицы.
ДСВ X может принимать значения: 0, 1, 2, 3, 4, 5. Вероятность появления герба в одном опыте р=1/2, непоявления q=1/2, n = 5.
Таким образом, выполняются условия применения формулы Бернулли.
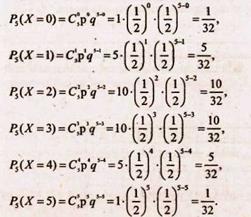
Имеем: Полученные данные можно представить в виде таблицы распределения:

Дискретная случайная величина может быть представлена в виде многоугольника распределения - фигуры, состоящей из точек (xi, pi), соединенных отрезками (рис. 8).
Над случайными величинами устанавливаются операции сложения и умножения.
1. Суммой двух случайных величин X и Y называется случайная величина, которая получается в результате сложения всех значений случайной величины X и всех значений случайной величины Y, соответствующие вероятности перемножаются.
2. Произведением двух случайных величин Х и Y называется случайная величина, которая получается в результате перемножения всех значений случайной величины X и всех значений случайной величины Y, соответствующие вероятности перемножаются.
Пример 1.2
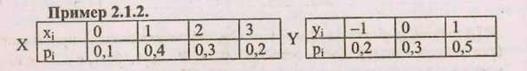
Найти: 1) Х + С, где С = 2; 2) X + У.
Решение.
1. Z = X+C, C=2.
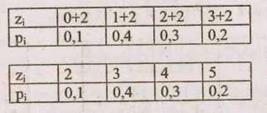
2. Z = X + Y.
| zi | 0-1 | 0+0 | 0+1 | 1-1 | 1+0 | 1+1 | 2-1 | 2+0 | 2+1 | 3-1 | 3+0 | 3+1 |
| pi | 0,02 | 0,03 | 0,05 | 0,08 | 0,12 | 0,2 | 0,06 | 0,09 | 0,15 | 0,04 | 0,06 | 0,1 |
Одинаковые значения СВ можно записать один раз, предварительно сложив соответствующие вероятности:

Контрольные вопросы:
- Что такое случайное событие?.
- Дайте классическое определение вероятности.
- В чём состоит схема Бернули? Запишите формулу Бернули.
- Что называется случайной величиной (СВ)?
- Виды СВ?
- В чём состоит закон распределения дискретных случайных величин?








