Тема: Случайные события и их вероятности. Случайные величины и законы их распределения.
Урок - лекция
Тема: Случайные события и их вероятности. Случайные величины и законы их распределения.
Цель: познакомиться с основными понятиями теории вероятности.
Задание: изучить материал урока и ответить на контрольные вопросы.
Ход урока
1. Изучение нового материала
События
Событие в теории вероятностей – это множество, состоящее из элементарных событий.
События обычно имеют свои словесные описания. Например, при бросании двух игральных костей можно рассматривать событие A, состоящее в суммарном выпадении четного числа очков, а при вытаскивании игральной карты из колоды событием является выпадение карты бубновой масти. Все эти события состоят из элементарных событий. Так, при бросании игральных костей событие A состоит из элементарных событий {1,1}, {1,3}, {1,5}, {2,2}, {2,4}, {2,6}, {3,1} {3,3}, {3,5}, {4,2}, {4,4}, {4,6}, {5,1}, {5,3}, {5,5}, {6,2}, {6,4}, {6,6}.
Достоверным событием называется событие, состоящее из всех элементарных событий.
Достоверное событие происходит всегда, поскольку в результате случайного выбора какое-то элементарное событие всегда реализуется. Обозначим достоверное событие буквой Ώ.
Невозможным событием называется событие, которое не может произойти никогда.
Обозначим его V . Оно представляет собой пустое множество элементарных событий.
Противоположным событию А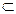 
Ώ событием называется событие 
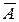, состоящее в том, что событие А не произошло.
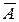состоит из элементарных событий, не входящих в А.
Суммой (или объединением) событий А и В называется событие А + В, состоящее в том, что из двух событий А и В происходит по крайней мере одно (либо А, либо В, либо А и В вместе).
Этому событию соответствует множество элементарных событий А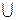 
В. Поэтому, иногда мы будем использовать знак объединения, вместо знака суммирования.
Пример. По мишени стреляют 3 раза. События А, В, С – попадание при 1-ом, 2-ом и 3 выстрелах соответственно. Сумма событий А, В и C означает хотя бы одно попадание.
Классическое определение вероятности
Пусть некоторый опыт может приводить лишь к одному из конечного множества результатов. Эти результаты будем называть элементарными исходами. Предположим, что элементарные исходы удовлетворяют следующим условиям:
1) образуют полную группу, т.е. в каждом испытании обязан появиться какой-нибудь из этих исходов;
2) попарно несовместны, т.е. два различных элементарных исхода не могут появиться в одном испытании;
3) равновозможные, т.е. шансы на появление у всех элементарных исходов одинаковы.
В этих условиях может использоваться классическое определение вероятности.
Определение: Элементарные исходы, в которых появляются интересующее нас событие, называются благоприятными этому событию.
Определение: Вероятностью события А называются число P(А), равное отношению числа исходов испытания, благоприятствующих событию А к общему числу исходов:
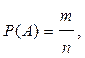где n – общее число исходов испытания, m – число исходов, благоприятствующих событию А.
Пример: Бросается один раз игральная кость. Какова вероятность выпадения нечетного числа очков?
Решение: Опыт состоит в бросании игральной кости 1 раз и наблюдении за числом очков, появившихся на верхней грани.
Все исходы опыта: 1, 2, 3, 4, 5, 6.
Число всех исходов: n = 6.
Рассмотрим событие А – выпало нечетное число очков. Исходы благоприятствующие А: 1, 3, 5.
Число исходов, благоприятствующих А : m = 3
.
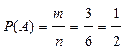