Лекция. Производная суммы, разности, произведения и частного функций
Производные основных элементарных функций.
План
1. Производная степенной функции.
2. Правила дифференцирования. Производная сложной функции.
3. Производные основных элементарных функций.
4. Таблица производных
1. Производная степенной функции.
Итак, на предыдущих занятиях нами были получены следующие формулы производных:
.
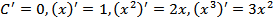
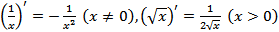Четыре последние формулы являются формулами производной степенной функции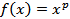 
для 
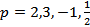. Их можно записать так:
,
.
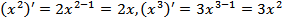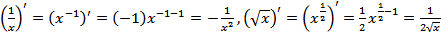Вообще, справедлива формула производной степенной функции для любого действительного показателя:
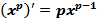. (1)
Эта формула применима при тех значениях x, при которых её правая часть имеет смысл.
Например,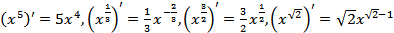 
.
Пример 1
Вычислить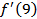 
, если 
.
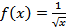Решение
.
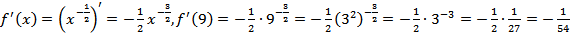Ответ: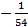 
Пользуясь формулам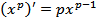и 
и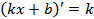 
, можно найти производные степенной и линейной функций, например 
.
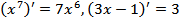В более сложных случаях, например при нахождении производной функции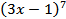 
, можно воспользоваться следующей формулой: 
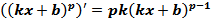. (2)
По формуле (2) при k = 3, b = -1, p = 7 имеем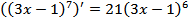 
.
2. Правила дифференцирования. Производная сложной функции.
При вычислении производной используются следующие правила дифференцирования суммы, произведения и частного:
1. Производная суммы равна сумме производных:
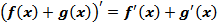(3)
Подробно это свойство производной формулируется так: если каждая из функци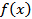й 
и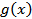 
имеет производную, то их сумма также имеет производную и справедлива формула (3).
Производная суммы нескольких функций равна сумме производных этих функций, производная разности равна разности производных.
Пример 2
Найдите производную функции:
1) 
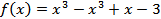; 2)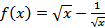 
.
Решение
1) 
;
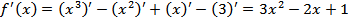2) 
.
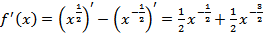Ответ: 1)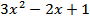 
; 2)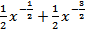 
.
2. Постоянный множитель можно вынести за знак производной:
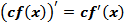(4)
Пример 3
Вычислить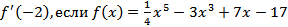 
.
Решение
,
.
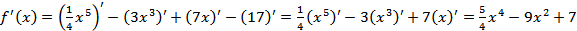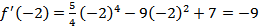Ответ: -9
3. Производная произведения:
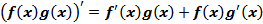(5)
Пример 3
Найдите производную функции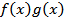 
, если 
.
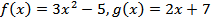Решение
По формуле (5) находим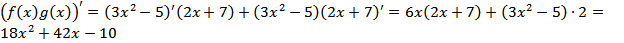 
.
Ответ: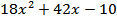 
4. Производная частного:
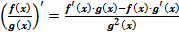(6)
Формулы (5) и (6) справедливы при условии, что функци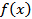и и 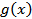имеют производную в точке x, причём в раенстве (6) 
.
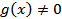Пример 4
Найдите производную функции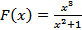 
.
Решение
Обозначим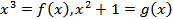 
. По формуле (6) находим 
.
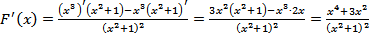Ответ: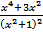 
Производная сложной функции.
Рассмотрим функция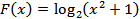 
. Эту функцию можно рассматривать как сложную функцию 
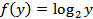, где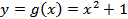 
, т.е. как функцию 
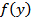, аргумент которой также является функцией 
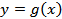. Иными словами, сложная функция – это функция от функции 
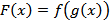. Производная сложной функции находится по формуле 
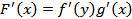, где 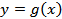, т.е. по формуле
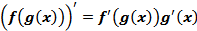. (7)
Рассмотрим примеры.
1) Пусть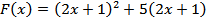 
.
Здесь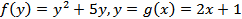 
.
По формуле (7) находим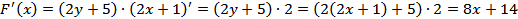 
.
2) Пусть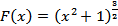 
. Здесь 
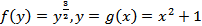. По формуле (7) находим
.
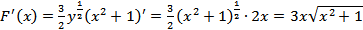3. Производные основных элементарных функций.
Элементарными функциями нвзывают степенную, показательную, логарифмическую и тригонометрические функции, а также из различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
Например, напряжение в цепи переменного тока выражается формулой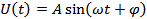 
; для нахождения силы тока 
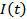нужно уметь находить производную 
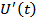, так как 
.
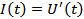1) Производная показательной функции.
Показательная функция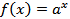 
, где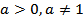 
, определена на всей числовой прямой и имеет производную в каждой её точке. Любую показательную функцию можно выразить через показательную функцию с основанием e по формуле 
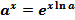, (8)
так как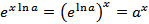 
. В курсе высшей математики доказывается, что функция 
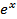обладает замечательным свойством: её производная также равна 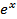, т.е.
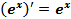(9)
Применяя правило дифференцирования сложной функции, получаем
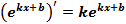(10)
Например,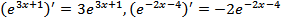 
.
Пример 5
Найдите производную функции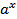 
, где .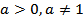
Решение
Используя формулы (8) и (10), находим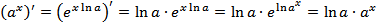 
.
Итак,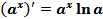 
(11)
Ответ: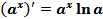
Например,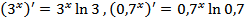 
.
2) Производная логарифмической функции.
Логарифмическую функцию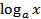 
с любым основанием 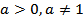можно выразить через логарифмическую функцию с основанием e с помощью формулы перехода
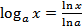. (12)
Производная функции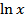 
выражается формулой 
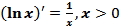. (13)
Применяя правило дифференцирования сложной функции, получаем
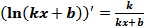. (14)
Например,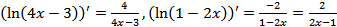 
.
Пример 6
Найти производную функции 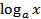, где .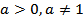
Решение
Используя формулы (12) и (13), находим
.
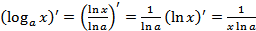Итак,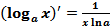 
. (15)
Ответ: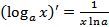 
3) Производные тригонометрических функций.
Справедливы следующие формулы:
; 
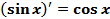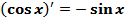. (16)
Применяя правило дифференцирования сложной функции, имеем следующие формулы
,
.
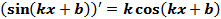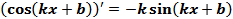Например,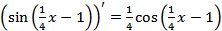 
,
.
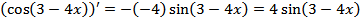Пример 7
Найдите производную функции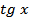 
.
Решение
Используя правило дифференцирования частного и формулы (16), находим
.
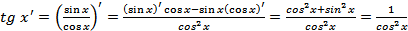Итак,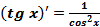 
. (17)
Ответ: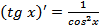 
Пример 8
Найдите производную функции:
1) 
;
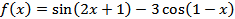2) 
;
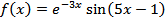3) 
.
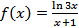Решение
1) 
;
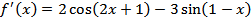2) 
;
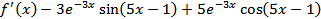3) 
.
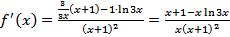Пример 9
Найдите значение x, при которых значение производной функции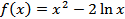 
равно нулю; положительно; отрицательно.
Решение
Найдем производную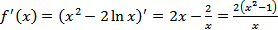 
.
Заметим, что равенство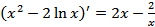 
справедливо при тех значениях x, при которых обе части имеют смысл, т.е. при 
.
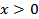Выражение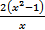 
равно нулю при 
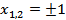, положительно на промежутках
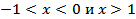; отрицательно на промежутках 
.
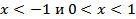Так как 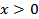, то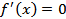 
только при 
; 
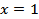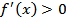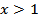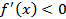при 
; 
при
.
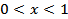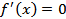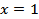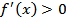Ответ: при 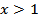; 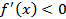при ; при 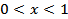.