Работа 4. Разработка и исследование модели и алгоритма формирования плана работы проектной организации в условиях асоиу
Цель работы – ознакомиться с постановкой и методами решения задачи формирования плана работы проектной организации, предложить, реализовать на ЭВМ и исследовать эффективность предложенной модели и алгоритма ее решения на конкретном числовом примере.
4.1. Порядок выполнения работы
1. Ознакомиться с постановкой задачи формирования плана работы проектной организации.
2. Изучить рассмотренные в лабораторной работе модели решения задачи формирования плана работы проектной организации в условиях АСОИУ.
3. Предложить свою содержательную постановку задачи формирования тематического плана работы проектной организации.
4. Предложить критерий выбора составленного плана работы проектной организации, дать ему формализованное представление.
5. Определить систему ограничений, налагаемых на составленный план работы проектной организации, дать ей формализованное представление.
6. Составить математическую модель формирования плана работы проектной организации, используя результаты выполнения п. 4 и п. 5, согласовать ее с преподавателем.
7. Разработать алгоритм решения модели формирования плана работы проектной организации, согласовать его с преподавателем.
8. Реализовать разработанный алгоритм в виде программы для ПЭВМ, проверить работоспособность разработанной программы на контрольном примере.
9. Составить отчет по лабораторной работе, в котором отразить:
 содержательную постановку и математическую модель решения поставленной задачи;
содержательную постановку и математическую модель решения поставленной задачи;
 рассмотренные примеры выбранных разработок и критерии их оценки, полученные по результатам выполнения лабораторной работы 3, для контрольного примера;
рассмотренные примеры выбранных разработок и критерии их оценки, полученные по результатам выполнения лабораторной работы 3, для контрольного примера;
 алгоритм решения модели формирования плана работы проектной организации;
алгоритм решения модели формирования плана работы проектной организации;
 программную реализацию разработанного алгоритма;
программную реализацию разработанного алгоритма;
 результаты машинных расчетов и их анализ.
результаты машинных расчетов и их анализ.
10. Ответить на контрольные вопросы.
4.2. Методические указания
4.2.1. Постановка задачи
Пусть к началу формирования тематического плана разрабатывающего предприятия (РП) для всех разработок, предполагаемых к выполнению в планируемом периоде, выполнен этап исходного планирования. Это означает, что для каждой разработки получена оценка эффективности, технического уровня разрабатываемого изделия или какая-либо другая количественная оценка, отражающая ее вклад в достижение целей РП.
Определены также нормативные (планируемые) затраты ресурсов по каждому этапу выполнения разработки, их предварительные (желательные) сроки завершения, а также принадлежность разработки к той или иной приоритетной группе. Кроме того, известны ресурсы основных подразделений РП, которыми оно располагает в каждом планируемом периоде рассматриваемого планового горизонта.
В этих условиях задача формирования тематического плана РП формулируется как задача нахождения таких сроков выполнения разработок, чтобы за рассматриваемый плановый горизонт, с одной стороны, максимизировать суммарную ценность включенных в тематический план работ, а с другой - обеспечить наиболее полную загрузку всех основных подразделений РП.
В такой постановке задачу формирования тематического плана можно рассматривать как задачу составления расписания.
В самом общем виде расписанием может быть назван документ, содержащий следующие сведения:
а) о количестве и номенклатуре выполняемых работ, включая их этапы;
б) о моментах начала и окончания каждой работы, определяющих их продолжительность;
в) о месте и технических средствах выполнения каждой работы;
г) о затратах времени и материальных ресурсов на проведение всей совокупности работ.
Наибольший интерес как методологический, так и в прикладном смысле представляет общая задача теории расписаний, которая формулируется следующим образом.
Имеется производственная система (рис.4.1), состоящая из 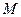 разнотипных
разнотипных 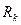 - канальных
- канальных 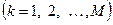 участков и
участков и 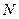 работ, каждая из которых должна выполняться в указанной системе и, следовательно, распадается на М этапов.
работ, каждая из которых должна выполняться в указанной системе и, следовательно, распадается на М этапов.
Участок 1 Участок 2 Участок М
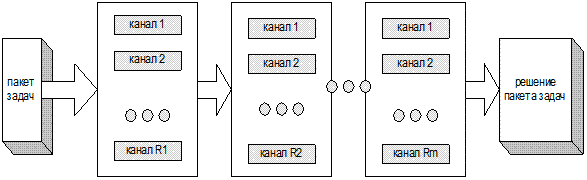
Рис.4.1
Заданы длительности проведения всех этапов каждой работы (матрица времен 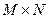 ) и условия ограничения, определяющие специфику отношений между операциями в рамках рассматриваемого технологического процесса (приоритетность, необходимость ожидания и т.п.).
) и условия ограничения, определяющие специфику отношений между операциями в рамках рассматриваемого технологического процесса (приоритетность, необходимость ожидания и т.п.).
Требуется составить план проведения работ с минимальным полным временем занятости системы от момента начала первой до момента завершения последней работы.
Трудности решения общей задачи таковы, что точный оптимум не удается найти даже в случаях, когда нет ограничений, сравнительно не велико количество работ и так далее. Причины этого заключаются в сложности структуры расписаний (дискретность, многовариантность), в отсутствии условий существования экстремума (приходится применять прямые методы его поиска), в несовершенстве оценок сходимости алгоритмов (часто исследователи ограничиваются просто набором статистик).
Следствием этого является разнообразие подходов к проблеме и признания достаточности приближенных результатов во многих практических ситуациях.
Ниже будут рассмотрены три возможные формализованные постановки задачи составления расписания применительно к проблеме формирования тематического плана разрабатывающего предприятия.
4.2.2. Постановка и формализация задачи на основе линейного программирования с булевыми переменными
Для формализации этой задачи введем следующие обозначения:
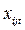 - переменная, равная 1, если в период t , t =
- переменная, равная 1, если в период t , t = 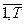 , для выполнения i-й разработки (НИР или ОКР) выбран j-й вариант, и равная 0 в противном случае;
, для выполнения i-й разработки (НИР или ОКР) выбран j-й вариант, и равная 0 в противном случае;
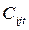 - количественная оценка (важность) j-го варианта i-й разработки (например, оценка технического уровня) при условии начала ее выполнения в период t ;
- количественная оценка (важность) j-го варианта i-й разработки (например, оценка технического уровня) при условии начала ее выполнения в период t ;
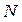 - число рассматриваемых разработок;
- число рассматриваемых разработок;
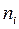 - число альтернативных вариантов i-й разработки;
- число альтернативных вариантов i-й разработки;
Т - плановый горизонт, на котором решается задача определения сроков начала выполнения рассматриваемых разработок;
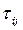 - продолжительность выполнения j-го варианта
- продолжительность выполнения j-го варианта 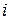 - й разработки.
- й разработки.
Будем считать, что продолжительности выполнения всех вариантов выполнения разработок одинаковы и равны Q, где Q 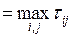 .
.
Пусть, наконец, 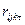 - количество ресурсов k - го вида (k =
- количество ресурсов k - го вида (k = 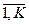 ), необходимое в t - й (t =1, 2, … Q ) период выполнения j-го варианта i-й разработки.
), необходимое в t - й (t =1, 2, … Q ) период выполнения j-го варианта i-й разработки.
В условиях РП перегрузку одних подразделений в ряде случаев можно устранить путем передачи части запланированных им работ другим родственным подразделениям.
Пусть 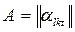 - квадратная матрица, элемент которой
- квадратная матрица, элемент которой 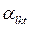 равен 1, если ресурс l -го подразделения РП может быть использован в период t для возмещения дефицита ресурса в k -м подразделении и равен 0 в противном случае. Обозначим через
равен 1, если ресурс l -го подразделения РП может быть использован в период t для возмещения дефицита ресурса в k -м подразделении и равен 0 в противном случае. Обозначим через 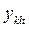 количество ресурсов k-го подразделения, которое может быть передано в l-е подразделение в период t , а через
количество ресурсов k-го подразделения, которое может быть передано в l-е подразделение в период t , а через 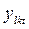 - количество ресурса l -го подразделения, идущее на покрытие дефицита ресурса в k-м подразделении. Тогда в t - й период имеющийся ресурс k-го подразделения может быть увеличен на величину
- количество ресурса l -го подразделения, идущее на покрытие дефицита ресурса в k-м подразделении. Тогда в t - й период имеющийся ресурс k-го подразделения может быть увеличен на величину 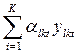 и уменьшен на величину
и уменьшен на величину 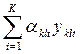 , т.е. может составлять
, т.е. может составлять
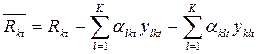 ,
,
где 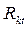 - имеющиеся производственные возможности k-го подразделения в период t ,
- имеющиеся производственные возможности k-го подразделения в период t , 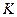 - число подразделений РП.
- число подразделений РП.
Из k-го подразделения в l-е подразделение могут быть переданы не все ресурсы этого k-го подразделения, а только некоторая часть. Поэтому 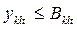 , где
, где 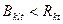 -максимально возможное количество ресурса k-го подразделения, которое может быть передано в l-е подразделение.
-максимально возможное количество ресурса k-го подразделения, которое может быть передано в l-е подразделение.
Задачу формирования тематического плана можно теперь формализовать следующим образом (с учетом вышесказанного):
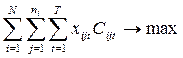 (4.1)
(4.1)
при следующих ограничениях по ресурсным возможностям 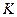 подразделений РП:
подразделений РП:
для первого планового периода:
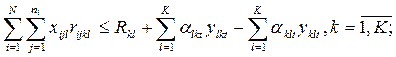 (4.2)
(4.2)
для второго планового периода с учетом затрат ресурсов на отобранные в этом втором периоде разработки, а также ресурсы, необходимые на выполнение тех разработок, которые были отобраны на предыдущем, т.е. первом периоде,
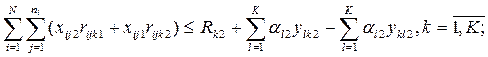 (4.3)
(4.3)
для третьего планового периода с учетом затрат ресурсов на отобранные в этом уже третьем периоде разработки, а также ресурсы, необходимые на выполнение разработок, отобранных на предыдущих, т.е. первом и втором периодах,
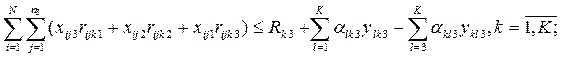 (4.4)
(4.4)
для ( Q - 1) - го периода с учетом аналогичных рассуждений
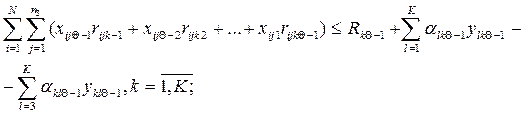 (4.5)
(4.5)
для периода t = Q ,…,Т
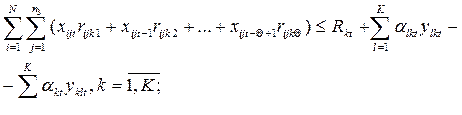 (4.6)
(4.6)
Полученную систему неравенств необходимо еще дополнить следующими неравенствами:
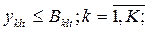
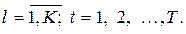 (4.7)
(4.7)
Система неравенств (4.7) отражает тот факт, что количество ресурсов, передаваемых из k-го подразделения в 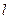 -е, ограничено некоторым заданным значением.
-е, ограничено некоторым заданным значением.
Кроме того, следует ввести систему неравенств, отражающих необходимость выполнения только одного варианта разработки, причем этот вариант может быть начат только один раз. Это условие записывается следующим образом:
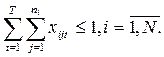 (4.8)
(4.8)
Наконец, может оказаться, что для некоторых разработок время начала выполнения должно наступить не позднее заданного периода. Обозначим множество таких разработок через W , а соответствующие крайние периоды начала выполнения – через 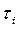 . Тогда дополнительная система ограничений примет вид
. Тогда дополнительная система ограничений примет вид
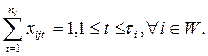 (4.9)
(4.9)
Задача (4.1) – (4.9) относится к задаче линейного программирования с булевыми переменными, для которой разработаны алгоритмы ее решения. Однако их практическое применение в ввиду большой размерности задачи в реальных условиях РП затруднительно. Это приводит к необходимости упрощения задачи, привлечения к ее решению эвристических методов и процедур.
4.2.3. Двухуровневое распределение ресурсов между разработками методом динамического программирования
Процесс решения задачи распределения ресурсов между разработками можно представить как двухуровневую систему принятия решений.
На первом уровне решается задача оптимального распределения ресурсов между отдельными работами данной разработки с целью обеспечения максимальной вероятности ее выполнения, а на следующем уровне решается аналогичная задача, но уже для всего множества разработок.
На первом уровне для каждой разработки 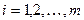 используется:
используется:
1) сетевой график работ, отражающий последовательность и взаимосвязь выполняемых работ;
2) выделенный на разработку обобщенный ресурс:
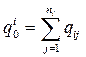 (4.10)
(4.10)
где j=1,2,…,ni – число работ i-й разработки в сетевом графике;
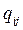 - количество обобщенного ресурса, выделенного на выполнение работы
- количество обобщенного ресурса, выделенного на выполнение работы 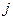 в i-й разработке;
в i-й разработке;
i=1,2,…,m - число разработок.
3) 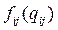 – вероятность выполнения каждой отдельной работы j разработки i в зависимости от количества выделенного на нее ресурса
– вероятность выполнения каждой отдельной работы j разработки i в зависимости от количества выделенного на нее ресурса 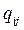 .
.
Необходимо определить максимальную общую вероятность выполнения всех работ разработки в заданное время и соответствующее ей распределение обобщенного ресурса между работами, т.е. необходимо решить следующую оптимизационную задачу:
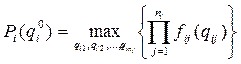 , (4.11)
, (4.11)
при условии, что выполняется следующее ограничение
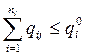 (4.12)
(4.12)
Как показывает опыт и проведенные исследования, зависимость вероятности выполнения работы j разработки i от количества выделенного на нее ресурса 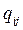 описывается следующей формулой:
описывается следующей формулой:
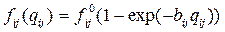 , (4.13)
, (4.13)
где 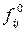 - вероятность выполнения работы
- вероятность выполнения работы 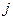 разработки
разработки 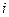 при максимальном количестве выделенных на эту работу ресурсов;
при максимальном количестве выделенных на эту работу ресурсов;
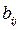 - экспериментально устанавливаемый коэффициент, отражающий влияние единицы выделенного ресурса на вероятность выполнения работы
- экспериментально устанавливаемый коэффициент, отражающий влияние единицы выделенного ресурса на вероятность выполнения работы 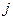 разработки
разработки 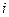 в заданные сроки.
в заданные сроки.
Для решения задачи (4.11) - (4.13) воспользуемся методом динамического программирования.
Пусть 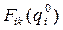 – максимальная вероятность выполнения в срок
– максимальная вероятность выполнения в срок 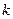 первых работ i–й разработки при условии, что на нее выделено
первых работ i–й разработки при условии, что на нее выделено 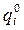 ресурсов (k=1,2,…,ni ):
ресурсов (k=1,2,…,ni ):
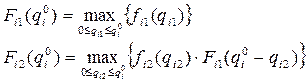
………………………………………… (4.14)
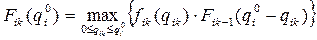
…………………………………………
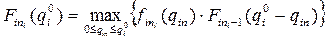
После построения функций 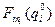 для всех i=1,2,…,m и разных значений
для всех i=1,2,…,m и разных значений 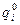 решаем задачу второго уровня с целью получения максимальной вероятности выполнения в срок всех разработок тематического плана. Для этого решаем следующую задачу:
решаем задачу второго уровня с целью получения максимальной вероятности выполнения в срок всех разработок тематического плана. Для этого решаем следующую задачу:
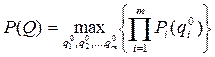 , (4.15)
, (4.15)
при ограничении:
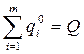 (4.16)
(4.16)
В выражении (4.15) 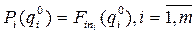 .
.
Формально задача (4.14)-(4.16) ничем не отличаются от задачи (4.11) - (4.13) и может быть также решена методом динамического программирования. Для этого пусть 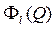 есть максимальная вероятность выполнения первых l разработок , l=1,2,…,m.
есть максимальная вероятность выполнения первых l разработок , l=1,2,…,m.
Тогда имеем:
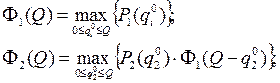
…………………………………….….. (4.17)
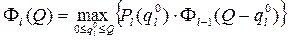
………………………………………...
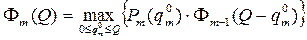
4.2.4. Модель включения в тематический план инициативных разработок с учетом взаимозаменяемости ресурсов
После включения в тематический план всех директивных разработок может оказаться, что еще остались ресурсы в количестве 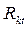 , где
, где 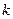 - номер вида ресурса,
- номер вида ресурса, 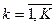 ,
, 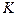 - число различных видов ресурсов,
- число различных видов ресурсов, 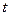 - номер периода,
- номер периода, 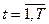 ,
, 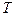 - плановый горизонт, на котором решается задача формирования тематического плана.
- плановый горизонт, на котором решается задача формирования тематического плана.
Пусть 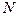 - число инициативных разработок портфеля заказов. Для каждой такой разработки определены количественная оценка эффективности (важности)
- число инициативных разработок портфеля заказов. Для каждой такой разработки определены количественная оценка эффективности (важности) 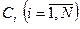 , требуемое количество ресурсов
, требуемое количество ресурсов 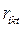
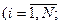
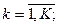
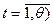 , где
, где 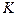 - число различных видов ресурсов,
- число различных видов ресурсов, 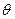 - продолжительность выполнения всех инициативных разработок.
- продолжительность выполнения всех инициативных разработок.
Необходимо определить, какие разработки из числа инициативных следует включить в тематический план, обеспечив при этом максимальную суммарную важность всех выбранных разработок с учетом возможности замены одного вида ресурсов другим. Эту задачу можно решить следующим образом.
Назовем вариантом включения разработок в тематический план любое сочетание их из общего списка 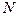 конкурирующих разработок. Так как количество вариантов
конкурирующих разработок. Так как количество вариантов 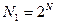 , то для представления любого номера
, то для представления любого номера 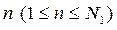 в двоичном коде необходимо
в двоичном коде необходимо 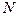 двоичных цифр.
двоичных цифр.
Условимся, что каждый разряд двоичного числа соответствует одной разработке, и тогда, если в этом разряде находится 1, то разработка включается в план, если 0 – нет. Таким образом, зная номер варианта, легко определить номера входящих в него разработок, их общую ценность и требуемые ресурсы.
Для осуществления варианта необходимо, чтобы на каждом периоде планирования существовало распределение взаимозаменяемых ресурсов предприятия, удовлетворяющее запросы всех разработок этого варианта. Для определения требований варианта по всем типам ресурсов на каждом периоде планирования просуммируем запросы всех ресурсов.
Для грубой оценки осуществимости варианта можно сравнить сумму его запросов по типам ресурсов на каждом плановом периоде 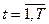 с суммой запасов всех ресурсов предприятия на этом периоде.
с суммой запасов всех ресурсов предприятия на этом периоде.
Рассмотрим более детально распределение ресурсов на некотором периоде планирования 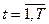 .
.
Пусть имеется всего 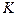 типов ресурсов;
типов ресурсов; 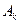 - суммарный запрос всех тем варианта
- суммарный запрос всех тем варианта 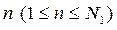 на использование
на использование 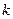 - го типа ресурса
- го типа ресурса 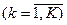 ;
; 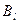 - величина запасов предприятия по
- величина запасов предприятия по 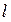 - му типу ресурсов
- му типу ресурсов 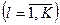 ;
; 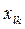 - объемы
- объемы 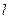 -го типа ресурсов, идущие на удовлетворение потребностей варианта в ресурсах
-го типа ресурсов, идущие на удовлетворение потребностей варианта в ресурсах 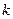 - го типа;
- го типа; 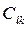 - затраты на использование
- затраты на использование 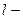 го типа ресурсов вместо
го типа ресурсов вместо 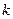 - го типа;
- го типа; 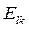 - эффективность замены
- эффективность замены 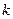 - го типа ресурса
- го типа ресурса 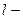 м типом, т.е. количество
м типом, т.е. количество 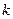 - го типа ресурса, эквивалентное единице
- го типа ресурса, эквивалентное единице 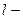 го типа ресурса.
го типа ресурса.
При этих обозначениях задача распределения ресурсов состоит в отыскании неотрицательных значений переменных 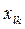 , обеспечивающих минимальные затраты на реализацию варианта при следующих условиях:
, обеспечивающих минимальные затраты на реализацию варианта при следующих условиях:
 удовлетворение запросов варианта по всем типам ресурсов, т.е.
удовлетворение запросов варианта по всем типам ресурсов, т.е.
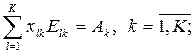 (4.18)
(4.18)
 ограниченность ресурсов предприятия, т.е.
ограниченность ресурсов предприятия, т.е.
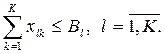 (4.19)
(4.19)
Кроме того, по смыслу задачи
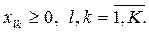 (4.20)
(4.20)
Критериальная функция модели, минимизирующая общие затраты, имеет следующий вид:
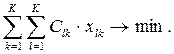 (4.21)
(4.21)
Задача (4.18) – (4.21) является задачей линейного программирования, и, в частности, при 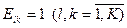 относится к классу открытых транспортных задач. Ее можно решить известными методами линейного программирования.
относится к классу открытых транспортных задач. Ее можно решить известными методами линейного программирования.
В практике тематического планирования проектной организации после включения в план директивных разработок число конкурирующих инициативных разработок обычно невелико, в пределах 10 -12. При большом числе их можно разделить на приоритетные группы важности, актуальности. Поэтому число возможных вариантов включения разработок в тематический план 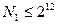 , и все эти варианты можно рассмотреть непосредственно и сравнить с помощью ЭВМ.
, и все эти варианты можно рассмотреть непосредственно и сравнить с помощью ЭВМ.
На этом основан следующий алгоритм направленного перебора формирования тематического плана проектной организации.
1. Для каждого варианта определяется суммарная важность входящих в него вариантов.
2. Все варианты сортируются в порядке убывания их важности. Если все варианты уже просмотрены, то алгоритм заканчивает работу.
3. Последовательно просматриваются все варианты, начиная с первого. Производится грубая оценка осуществимости варианта, затем с помощью решения модели (4.18) – (4.21) определяется распределение ограниченных ресурсов проектной организации, удовлетворяющее запросы всех разработок этого варианта. Если такое распределение найдено для всех периодов 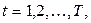 то вариант считается оптимальным и входящие в него разработки включаются в тематический план. Если же такого распределения нет или вариант оказывается неосуществимым даже при грубой оценке, то рассматривается следующий вариант из проранжированного по важности списка. Если все варианты просмотрены, то выполняется следующий пункт.
то вариант считается оптимальным и входящие в него разработки включаются в тематический план. Если же такого распределения нет или вариант оказывается неосуществимым даже при грубой оценке, то рассматривается следующий вариант из проранжированного по важности списка. Если все варианты просмотрены, то выполняется следующий пункт.
4. Сроки начала выполнения инициативных разработок, не включенных в план, увеличиваются на один интервал планируемого горизонта, после чего выполняется пункт 2.
4.3. Контрольные вопросы
1. Как формулируется общая задача составления расписания, как она трансформируется применительно к задаче формирования тематического плана проектной организации?
2. В чем состоят особенности формирования тематического плана проектной организации, как они могут формализоваться?
3. Какие критерии оптимизации можно предложить для задачи формирования тематического плана проектной организации?
4. Какие ограничения следует ввести в математическую модель формирования тематического плана проектной организации?
5. Какие методы и алгоритмы можно предложить для решения задачи формирования тематического плана проектной организации?
6. В чем состоит различие между математическими моделями формирования тематического плана проектной организации, рассмотренными в методических указаниях и моделью, предложенной Вами?
7. К какому классу оптимизационных задач относится задача, предложенная Вами?
8. В чем состоит содержательный смысл критерия оптимизации в постановке задачи, предложенной Вами?
9. Каков содержательный смысл ограничений, содержащихся в сформулированной вами задачи оптимизации плана работы проектной организации?
Приложение
Функциональное моделирование
Проектирование АСОИУ предполагает восприятие окружающей среды субъектом, воздействующего на неё, в виде конкретизированного отображения, имеющего конечный объем информации. Субъект в данном случае может быть представлен в качестве системы, реализованной в технической среде вычислительных машин, или человеко-машинной системой.
Отображение реализуется путём построения модели (модельный подход). Степень детализации и адекватность модели обеспечивает целевую направленность и эффективность технологии взаимодействия субъекта с окружающей средой. Действие субъекта можно рассматривать как функцию.
Для выполнения определенной функции субъект должен иметь ресурсы для её выполнения и каналы (связи), через которые передаётся воздействие. Под ресурсом при этом, будем понимать информационные, материальные средства и возможности, а также различные организационные структуры.
Множества функций и ресурсов, их взаимосвязь между собой будем рассматривать как структуру.
Технология взаимодействия субъекта с окружающей средой в случае наличия функциональной модели предусматривает три вида воздействий: без учёта состояния окружающей среды; с учётом состояния окружающей среды без изменения внутренней структуры; на внутреннюю структуру субъекта. Воздействие субъекта чаще всего осуществляется в виде комбинации этих видов.
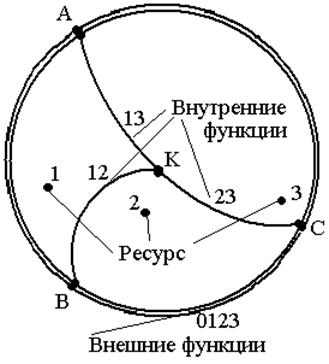
Пример. Структура взаимодействия при наличии трёх ресурсов может быть представлена так, как это показано на рис.1.
На рис.1 линиями обозначены множества внутренних функций, а двойными ¾ внешних функций. Области, ограниченные линиями ¾ ресурсы. Максимальное количество связей (границ) между ресурсами равно s = n – 1, где n ¾ количество ресурсов.
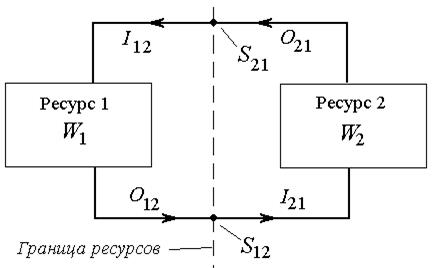
Функция взаимодействия ресурсов на границах, за исключением точек A , B, C и K, имеет вид, приведенный на рис.2. В этом случае имеем конфликт по ресурсам, так как сдвиг границы ресурсов в ту или иную сторону приводит к перераспределению ресурсов, при сохранении функций взаимодействия, как таковой. При этом возможно изменение её параметров и характера воздействия.
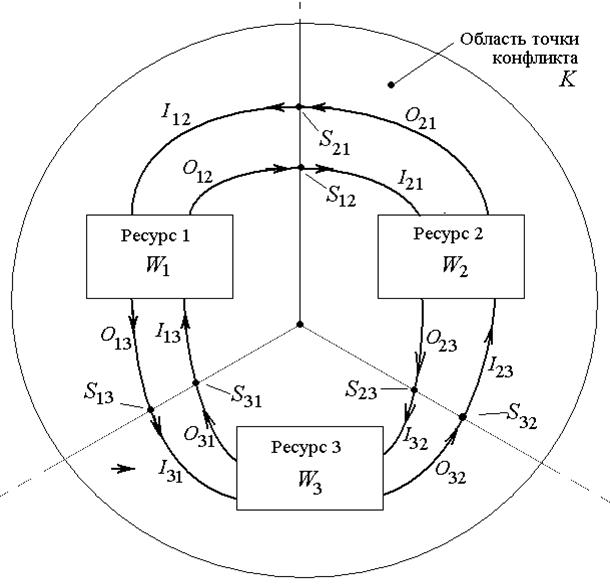
В точках исключения (точках конфликта ¾ A , B , C и K) функция взаимодействия имеет конфликт, как по ресурсу, так и по набору функций взаимодействия, за счет изменения или полного присвоения (исключения) последних (рис.3).
|
| Рис.1. Структура взаимодействия ресурсов |
|
| Рис.2. Структура функции взаимодействия ресурсов: I12 ¾ входное воздействие на ресурс W1; I21 ¾ входное воздействие на ресурс W2; O12 ¾ выходное воздействие ресурса W1; O21 ¾ выходное воздействие ресурса W1; S12 ¾ функция связи, оператор преобразования выходного воздействия O12 в I21; S21 ¾ функция связи, оператор преобразования выходного воздействия O21 в I12. |
Поставим целевую задачу сокращения каналов воздействия. С точки зрения ресурса W1 в области точки конфликта K (рис.3) один из двух ресурсов в этой точке лишний, так как у ресурса W1 существуют два входа и два выхода воздействий. С целью сокращения каналов воздействия (точек связи Sij) он может поглотить один из ресурсов или объединить их. Аналогичные точки зрения других ресурсов приводит к столкновению их интересов (конфликту) в области точки конфликта.
Внутренний конфликт (точки внутренних функций и точка конфликта K) использует воздействия без учёта состояния внешней среды.
|
| Рис.3. Структура функции взаимодействия ресурсов в точке конфликта: I i j ¾ входное воздействие ресурса Wj на ресурс Wi i ¹ j, i , j = 1…3; Oij ¾ выходное воздействие ресурса Wi на ресурс Wj; Sij ¾ функция связи (точка связи), оператор преобразования выходного воздействия O ij в I ji. |
Если поставить задачу результата воздействия ¾ перераспределение ресурсов, то она распадается на две части: перераспределение внутренних и захват внешних или потеря внутренних ресурсов. При перераспределении меняется внутренняя структура, внешние функции не меняются, но связь их с внутренними ресурсами меняется. Потеря или захват приводят как к изменению внутренней структуры, так и внешних функций.
Лексический анализ функций взаимодействия позволяет использовать различные точки зрения для выявления конфликтов между ресурсами. Конфликту соответствует описание одного и того же действия антонимами. В нашем примере объединение ресурсов сторон конфликта может иметь следующие оценки действий.
| Действие | Точки зрения ресурсов (оценка действия) | ||
| W1 | W2 | W3 | |
| Присоединение части ресурса: W2 к W3; | Перераспределение | Потеря | Захват |
| W1 к W3 | Потеря | Перераспределение | Захват |
| Присоединение всего ресурса W2 к W3 | Объединение | Потеря | Захват |
| и т.д. | |||
В случае совпадения оценки действий со стороны ресурсов (совпадения точек зрения) возможно согласование и их действий.
Эффективное управление объектом возможно только при достаточно полном объеме информации, обеспечивающим достоверный прогноз, а также при наличии эффективных средств воздействия ресурса управления на управляемые ресурсы. В случае использования интеллектуальных систем это обеспечивается за счёт построения модели, отражающей внешние и внутренние взаимодействия и конфликты.
Отсюда наиболее важным этапом решения задачи проектирования АСОИУ является функциональное моделирование структуры взаимодействия субъекта с окружающей средой. В настоящее время существует множество подходов к его реализации, один из них реализован в методологии функционального моделирования IDEF0, а также IDEF3 и DFD.
Библиографический список
1. Советов Б.Я. Информационная технология. - М.: Высшая школа, 1994.
2. Заикин О.А., Советов Б.Я. Проектирование интегрированных систем обработки информации и управления. - М.: МГАП “Мир книги”, 1994.
3. Хетагуров А.Я. Основы проектирования управляющих вычислительных систем. - М.: Радио и связь, 1991, 286, Н, 1.
4. Марка Д.А., МакГоуэн К. Методология структурного анализа и проектирования. - М.: "МетаТехнология", 1993.
5. Горин С.В., Тандоев А.Ю. Применение CASE-средства Erwin 2.0 для информационного моделирования в системах обработки данных. – М.: "СУБД", 1995, №3.
6. Черемных С.В., Семенов И.О., Ручкин В.С. Моделирование и анализ систем. IDEF-технологии: практикум. - М.: Финансы и статистика, 2002.
7. Черемных С.В., Семенов И.О., Ручкин В.С. Структурный анализ систем. IDEF-технологии. - М.: Финансы и статистика, 2001.
8. Берж К. Теория графов и ее применение. – М.: ИЛ, 1962.
9. Кендалл М. Ранговые корреляции: Пер. с англ. – М.: Статистика, 1975.
10. Романов О.Т. Проектирование математического обеспечения АСУ разработками авиационной техники: Учебное пособие. – М.: МАИ, 1987.
Оглавление
Предисловие. 3
РАБОТА 1. ПРОЕКТИРОВАНИЕ ОРГАНИЗАЦИОННОЙ СТРУКТУРЫ РАЗРАБАТЫВАЕМОЙ АСОИУ 4
1.2. Порядок выполнения работы.. 4
1.3. Методические указания. 4
1.4. Контрольные вопросы.. 17
РАБОТА 2. ПОСТРОЕНИЕ И ИССЛЕДОВАНИЕ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ ОБЪЕКТА АВТОМАТИЗАЦИИ СРЕДСТВАМИ МЕТОДОЛОГИИ IDEF0. 18
2.1. Порядок выполнения работы.. 18
2.2. Методология функционального моделирования IDEF0. 18
2.2.1. Общие положения. 18
2.2.2. Определение стрелок на контекстной диаграмме. 29
2.2.3. Нумерация блоков и диаграмм.. 30
2.2.4. Другие диаграммы IDEF0. 31
2.3. Методические указания по выполнению лабораторной работы.. 35
2.3.1. Общее описание интерфейса BPwin. 35
2.3.2. Создание новой модели. 36
2.4. Контрольные вопросы.. 41
РАБОТА 3. ИССЛЕДОВАНИЕ МЕТОДА И АЛГОРИТМА ОПРЕДЕЛЕНИЯ ОБЪЕКТИВНОЙ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ЭФФЕКТИВНОСТИ ВЫПОЛНЕНИЯ ПРЕДСТОЯЩЕЙ РАЗРАБОТКИ 42
3.1. Порядок выполнения работы.. 42
3.2. Методические указания. 43
3.2.1. Постановка задачи. 43
3.2.2. Нахождение весовых коэффициентов относительной важности локальных критериев экспертным методом парных сравнений. 47
3.2.3. Определение степени согласованности мнений экспертов по количественным оценкам весовых коэффициентов относительной важности локальных критериев. 52
3.3. Контрольные вопросы.. 54
РАБОТА 4. РАЗРАБОТКА И ИССЛЕДОВАНИЕ МОДЕЛИ И АЛГОРИТМА ФОРМИРОВАНИЯ ПЛАНА РАБОТЫ ПРОЕКТНОЙ ОРГАНИЗАЦИИ В УСЛОВИЯХ АСОИУ.. 55
4.1. Порядок выполнения работы.. 55
4.2. Методические указания. 56
4.2.1. Постановка задачи. 56
4.2.2. Постановка и формализация задачи на основе линейного программирования с булевыми переменными. 58
4.2.3. Двухуровневое распределение ресурсов между разработками методом динамического программирования. 60
4.2.4. Модель включения в тематический план инициативных разработок с учетом взаимозаменяемости ресурсов. 62
4.3. Контрольные вопросы.. 65
Приложение. Функциональное моделирование. 66
Библиографический список. 70
Тем. план 2009, поз.13
Романов Олег Тимофеевич
Машкин Михаил Николаевич
Лабораторные работы
Проектирование автоматизированных
систем обработки информации и управления
Редактор Р.Н.Фурсова
Компьютерная вёрстка М.Н.Машкин
Сдано в набор . .200 . Подписано в печать . .200 .
Бумага офсетная. Формат 60х84 1/16. Печать офсетная.
Усл. печ. л. 4,5. Уч.–изд.л. , . Тираж 300 экз.
Зак. / 200.
Издательство МАИ‑ПРИНТ
(МАИ), Волоколамское ш., д.4, Москва, А‑80, ГСП‑3 125993
Типография Издательства МАИ
(МАИ) Волоколамское ш., д.4, Москва, А‑80, ГСП‑3 125993








