Работа 3. Исследование метода и алгоритма определения объективной количественной оценки эффективности выполнения предстоящей разработки
Цель работы – ознакомиться с постановкой и методом решения задачи определения объективной количественной оценки эффективности выполнения предстоящей разработки, основанным на обработке результатов экспертного опроса специалистов, реализовать этот метод на ПЭВМ и применить его к реальным условиям.
3.1. Порядок выполнения работы
1. Ознакомиться с постановкой задачи определения объективной оценки эффективности выполнения разработки.
2. Изучить рассмотренный в работе метод и алгоритм обработки результатов экспертного опроса специалистов, оценивающих относительную важность критериев, определяющих эффективность выполнения разработки.
3. Составить перечень локальных критериев оценки предстоящих разработок.
4. Провести экспертный опрос среди студентов группы (не менее 5 человек) с целью получения экспертных оценок локальных критериев эффективности предстоящей разработки. Состав группы экспертов согласовать с преподавателем.
5. Вычислить вручную значения коэффициентов относительной важности локальных критериев, ограничившись 5-6 итерациями.
6. Ввести полученные экспертные оценки в ЭВМ и получить результаты экспертного опроса. Если согласованность экспертов мала (коэффициент конкордации меньше 0.3), то провести повторный экспертный опрос, повторить п. 5 лабораторной работы.
7. Вычислить обобщенные оценки эффективности для разработок, определенных в п. 3 лабораторной работы.
8. Составить отчет по лабораторной работе, в котором отразить:
 постановку и метод решения задачи;
постановку и метод решения задачи;
 рассмотренные примеры выбранных разработок и критериев их оценки;
рассмотренные примеры выбранных разработок и критериев их оценки;
 результаты экспертного опроса;
результаты экспертного опроса;
 результаты машинных расчетов;
результаты машинных расчетов;
 количественные оценки разработок.
количественные оценки разработок.
9. Ответить на контрольные вопросы.
3.2. Методические указания
3.2.1. Постановка задачи
К началу формирования годового тематического плана работы проектной организации в ее распоряжении имеется набор разработок, которые могут быть включены в тематический план (так называемый «портфель заказов»). Чтобы определить, какие из этих разработок следует выполнять в планируемом периоде, необходимо определить их относительную важность. Это позволит в дальнейшем установить порядок включения разработок в тематический план.
Существуют различные подходы к определению важности разработки. Один из таких подходов, получивший достаточно широкое применение в практике работы проектных организаций, рассмотрен в данной лабораторной работе. Этот подход получил название шкальной модели количественных оценок разработок и предполагает выполнение следующих действий:
1. Определение перечня локальных критериев, по которым будут осуществляться количественные оценки каждой разработки портфеля заказов.
2. Определение уровней шкалирования (градации, изменения) выбранных локальных критериев.
3. Построение математической модели (формулы), позволяющей по результатам количественной оценки разработки по каждому из выбранных критериев получить итоговую обобщенную количественную оценку.
4. Определение весовых коэффициентов относительной важности выбранных локальных критериев.
5. Оценка каждой разработки портфеля заказов по локальным критериям согласно установленной в п. 2 шкале изменения.
6. Вычисление количественных оценок разработок по математической модели.
Анализ показывает, что в практике работы проектной организации используют свыше тридцати различных критериев оценки отдельных разработок.
Эти критерии можно разбить на следующие три категории:
А. Критерии, определяющие значимость разработок самих по себе, независимо от возможности и целесообразности их выполнения в проектной организации:
 актуальность;
актуальность;
 экономическая эффективность;
экономическая эффективность;
 новизна и перспективность;
новизна и перспективность;
 научный уровень;
научный уровень;
 технический уровень;
технический уровень;
 область применения;
область применения;
 спрос на разрабатываемое изделие;
спрос на разрабатываемое изделие;
 осуществимость, вероятность достижения успеха;
осуществимость, вероятность достижения успеха;
 конкурентоспособность;
конкурентоспособность;
Б. Критерии, определяющие возможность выполнения разработки проектной организацией:
 пригодность кадров для выполнения предлагаемой разработки;
пригодность кадров для выполнения предлагаемой разработки;
 пригодность экспериментально-производственной базы;
пригодность экспериментально-производственной базы;
 соответствие организационной структуры (необходимость организационных преобразований);
соответствие организационной структуры (необходимость организационных преобразований);
 сложность выполнения;
сложность выполнения;
 существование научно-технического задела;
существование научно-технического задела;
 необходимость привлечения сторонних организаций;
необходимость привлечения сторонних организаций;
 продолжительность выполнения разработки;
продолжительность выполнения разработки;
 требуемое количество разработчиков;
требуемое количество разработчиков;
 требуемые производственные мощности:
требуемые производственные мощности:
 стоимость выполнения;
стоимость выполнения;
 возможность обеспечения необходимыми материалами и покупными элементами;
возможность обеспечения необходимыми материалами и покупными элементами;
 возможности обеспечения необходимой информацией.
возможности обеспечения необходимой информацией.
В. Критерии, определяющие желательность включения разработки (заказа) в план:
 значимость для проектной организации;
значимость для проектной организации;
 соответствие текущим и перспективным планам развития проектной организации;
соответствие текущим и перспективным планам развития проектной организации;
 влияние на увеличение престижа организации;
влияние на увеличение престижа организации;
 влияние на увеличение темпов научно-технического прогресса проектной организации;
влияние на увеличение темпов научно-технического прогресса проектной организации;
 влияние на ускорение темпов выполнения других разработок;
влияние на ускорение темпов выполнения других разработок;
 возможности освоения разрабатываемого изделия серийными заводами;
возможности освоения разрабатываемого изделия серийными заводами;
 заинтересованность разработчиков в выполнении работ;
заинтересованность разработчиков в выполнении работ;
 взаимоотношения с организациями, образующими внешнее окружение предприятия.
взаимоотношения с организациями, образующими внешнее окружение предприятия.
Уровни градации критериев должны быть выбраны таким образом, чтобы они позволяли достаточно объективно и единообразно характеризовать каждую разработку по соответствующим критериям. После этого каждому уровню градации присваивается определенное число. Эту операцию называют шкалированием критерия, откуда и пошло наименование метода.
Обычно в качестве шкалы берут числа от 0 до 1, или от 0 до 10, или от 0 до 100. Эти числа обычно присваиваются таким образом, чтобы более благоприятному содержательному уровню градации соответствовало бы и большее число.
Построение модели для получения итоговой количественной оценки разработки по своей сути представляет собой процедуру конструирования формулы, позволяющей свести воедино оценки по множеству локальных критериев. Это требует глубокого проникновения в особенности процесса проведения разработок в проектной организации, ее текущих и перспективных целей и задач. По своей сути структура такой формулы должна в равной степени отражать две стороны: возможность выполнения в установленные сроки (осуществимость) и ценность (эффективность) в широком смысле этого слова. Так как низкая оценка по любому из критериев, характеризующих каждую из этих сторон работы, в этом случае приводит к низкой интегральной оценке работы даже при высокой оценке по другому критерию, то формула для получения этой интегральной оценки обычно имеет следующий вид:
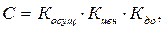
где 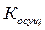 – количественная оценка разработки по критерию осуществимости;
– количественная оценка разработки по критерию осуществимости;
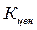 – количественная оценка разработки по критерию ценности для проектной организации;
– количественная оценка разработки по критерию ценности для проектной организации;
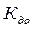 - количественная оценка работы по критерию достоверности сделанной оценки. зависящая от того, на каком этапе осуществляется эта оценка, выполняется ли оценка на стадии проработки технического задания или технического предложения, на стадии эскизного или технического проекта или на стадии рабочего проектирования.
- количественная оценка работы по критерию достоверности сделанной оценки. зависящая от того, на каком этапе осуществляется эта оценка, выполняется ли оценка на стадии проработки технического задания или технического предложения, на стадии эскизного или технического проекта или на стадии рабочего проектирования.
Структура формул для получения числовых значений 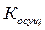 и
и 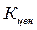 предполагает существование критических критериев, нулевая оценка по которым приводит к нулевой оценке разработки по интегральному критерию.
предполагает существование критических критериев, нулевая оценка по которым приводит к нулевой оценке разработки по интегральному критерию.
Такими критическими критериями, например, могут быть:
 продолжительность выполнения разработки;
продолжительность выполнения разработки;
 прогрессивность разработки;
прогрессивность разработки;
 заинтересованность генеральных разработчиков изделий в проведении данной разработки и т.п.
заинтересованность генеральных разработчиков изделий в проведении данной разработки и т.п.
Поэтому формулы количественных оценок работ по критериям осуществимости и ценности, как правило, имеют следующий вид:
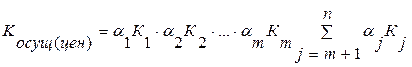 ,
,
где К1…К m – оценка работы по критическим критериям;
К m +1 …К n – оценка работы по остальным критериям;
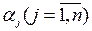 - весовые коэффициенты при количественных оценках
- весовые коэффициенты при количественных оценках
по критериям, показывающим их относительный вклад в
оценку разработки;
n – количество критериев работ для получения 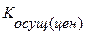 .
.
Весовые коэффициенты 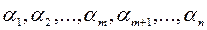 при количественных оценках по соответствующим критериям получают путем экспертного опроса специалистов предприятия.
при количественных оценках по соответствующим критериям получают путем экспертного опроса специалистов предприятия.
В качестве примера шкальной модели приведем следующую формулу для получения количественной оценки работы:
К = 100 × Косущ × Кцен × Кдо ,
где Косущ – оценка работы по критерию ее осуществимости;
Кцен – оценка работы по критерию ее ценности;
Кдо ×- оценка работы по критерию достоверности выполненной оценки.
При этом оценки по критериям Косущ и Кцен вычисляются по формулам:
Косущ=0,16 Кди+0,11 Ком+0,13 Коэ+0,15 Кдп+0,09 Кид+0,15 ос+
+0,1Кэб+0,11 Кпб;
Кцен= Кпр Кзо Кпв(0,27 Квп+0,26 Коп+0,24 Ксп+0,23 Кко),
где Кди – оценка по критерию достаточности научно-технической
информации;
Ком – оценка по критерию обеспеченности материалами;
Коэ – оценка по критерию обеспеченности элементами;
Кдп – оценка по критерию достоверности планирования;
Кид – оценка по критерию достоверности исходных данных;
Кос – оценка по критерию обеспечения специалистами;
Кэб – оценка по критерию пригодности экспериментальной
базы;
Кпб – оценка по критерию пригодности производственной базы;
Кпр – оценка по критерию прогрессивности;
Кзо – оценка по критерию заинтересованности других организаций;
Квп – оценка по критерию влияния на перспективный план;
Коп – оценка по критерию области применения;
Ксп – оценка по критерию серийного освоения;
Кко – оценка по критерию комплексности решения
научно-технических проблем.
Весовые коэффициенты в примере при соответствующих локальных критериях получены экспериментальным путем.
3.2.2.Нахождение весовых коэффициентов относительной важности локальных критериев экспертным методом парных сравнений
Сущность экспертного метода парных сравнений применительно к задаче нахождения весовых коэффициентов относительной важности локальных критериев оценки разработок состоит в следующем.
Группе экспертов, состоящей из М ведущих специалистов проектной организации, предлагается на рассмотрение и анализ перечень ранее определенных локальных критериев. Каждому эксперту с номером m (m =1,2,…, M) предлагается сравнить все возможные пары этих критериев и определить для каждой из пар, какой критерий более предпочтителен (более важен), чем другой.
Степень предпочтительности эксперт с номером m устанавливает путем задания каждой паре критериев с номерами 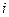 и
и 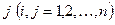 , где
, где 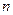 – общее число выбранных локальных критериев, числа
– общее число выбранных локальных критериев, числа 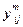 по следующей формуле:
по следующей формуле:
|
| если критерий с номером i более предпочтителен, чем критерий с номером j; | |
| если критерии с номерами i и j по важности равноценны; | (3.1) | |
| если критерий с номером i менее предпочтителен, чем критерий с номером j. |
Каждая пара критериев может сравниваться дважды или только один раз. Последний вариант на практике встречается чаще. Он предполагает, что числа 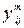 и
и 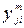 связаны следующим равенством:
связаны следующим равенством:
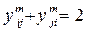 . (3.2)
. (3.2)
Полученные данные эксперт сводит в таблицу следующего вида (табл. 3.1)
Таблица 3.1
Результаты экспертного опроса специалиста ____________________________
(Ф.И.О)
Присвоенный эксперту номер _________
| Номер критерия | Наименование критерия | Порядковый номер критерия | |||||||
| 1 | 2 |

|
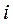
|

|
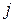
|

|
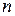
| ||
| 1 | Обеспеченность материалами | 1 | 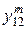
| 
| 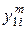
| 
| 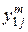
| 
| 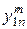
|
| 2 | Достоверность информации | 2- 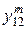
| 1 | 
| 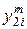
| 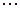
| 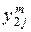
| 
| 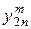
|
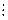
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
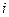
| Прогрессивность | 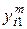 
| 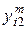
| 
| 1 | 
| 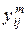
| 
| 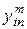
|
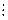
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
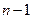
| Возможности производства | 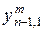
| 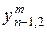
| 
| 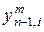
| 
| 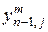
| 
| 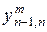
|
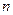
| Получение прибыли | 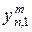
| 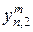
| 
| 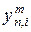
| 
| 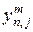
| 
| 1 |
После получения от каждого эксперта значений 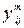 осуществляется обработка этих данных с целью установления коэффициентов относительной важности критериев.
осуществляется обработка этих данных с целью установления коэффициентов относительной важности критериев.
Одним из методов нахождения этих коэффициентов является метод, основанный на так называемой задаче о лидере. Суть применения этого метода к задаче нахождения искомых коэффициентов для большей определенности рассмотрим на следующем примере.
Предположим, что эксперту необходимо определить систему предпочтения четырех критериев 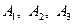 и
и 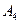 . В результате экспертного опроса получены данные, которые сведены в табл. 3.2.
. В результате экспертного опроса получены данные, которые сведены в табл. 3.2.
Таблица 3.2
| Критерии | А1 | А2 | А3 | А4 |
| А1 | 1 | 2 | 0 | 2 |
| А2 | 0 | 1 | 1 | 2 |
| А3 | 2 | 1 | 1 | 1 |
| А4 | 0 | 0 | 1 | 1 |
В табл.3.2 в клетке на пересечении, например, первой строки и второго столбца стоит значение 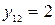 , т.е. критерий А1 предпочтительнее критерия А2, при этом в клетке на пересечении второй строки и первого столбца стоит значение
, т.е. критерий А1 предпочтительнее критерия А2, при этом в клетке на пересечении второй строки и первого столбца стоит значение 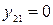 в соответствии с формулой (2).
в соответствии с формулой (2).
Аналогично в клетке на пересечении второй строки и третьего столбца стоит значение 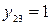 , т.е. критерии А2 и А3 равноценны, при этом согласно формуле (2) в клетке на пересечении третьей строки и второго столбца стоит значение
, т.е. критерии А2 и А3 равноценны, при этом согласно формуле (2) в клетке на пересечении третьей строки и второго столбца стоит значение 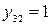 .
.
Все элементы главной диагонали формально полагают равными 1, так как очевидно, что каждый критерий по отношению к самому себе равноценен.
Подсчитаем для каждого критерия А i (i =1,2,3,4) количество набранных им (критерием) очков как сумму чисел, стоящих в i -й строке:
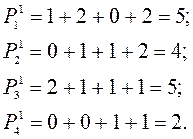
Разделив числа 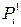 (i =1,2,3,4) на их сумму, можно получить коэффициенты относительной важности критериев
(i =1,2,3,4) на их сумму, можно получить коэффициенты относительной важности критериев 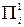 первой итерации (для простоты ограничившись четырьмя знаками после запятой):
первой итерации (для простоты ограничившись четырьмя знаками после запятой):
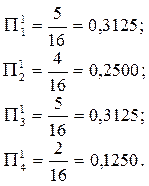
Полученные величины можно было бы взять в качестве искомых коэффициентов относительной важности критериев. Однако их еще можно уточнить. Для этого вычислим для каждого критерия величины 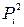 (i =1,2,3,4) путем сложения очков тех критериев, которые он превосходит:
(i =1,2,3,4) путем сложения очков тех критериев, которые он превосходит:
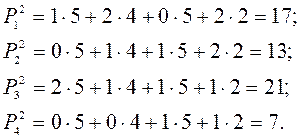
Разделив числа 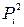 (i =1,2,3,4) на их сумму, найдем коэффициенты относительной важности второй итерации:
(i =1,2,3,4) на их сумму, найдем коэффициенты относительной важности второй итерации:
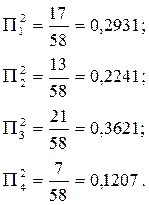
Как видно из приведенных расчетов, хотя коэффициенты относительной важности первой итерации для критериев А1 и А3 совпадали, этого уже не наблюдается у коэффициентов относительной важности второй итерации, где 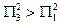 . И это представляется более правильным, так как хотя критерий А1 и превосходит два критерия А2 и А4, а критерий А3 – только один, но этим как раз и является критерий А1. Поэтому действительно, вправе требовать, чтобы коэффициент относительной важности критерия А3 был бы больше соответствующего коэффициента критерия А1, что как раз и имеет место, т.е.
. И это представляется более правильным, так как хотя критерий А1 и превосходит два критерия А2 и А4, а критерий А3 – только один, но этим как раз и является критерий А1. Поэтому действительно, вправе требовать, чтобы коэффициент относительной важности критерия А3 был бы больше соответствующего коэффициента критерия А1, что как раз и имеет место, т.е. 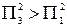 .
.
Можно продолжить эту процедуру и найти коэффициенты относительной важности третьей итерации. Для этого вычислим вначале величины 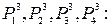
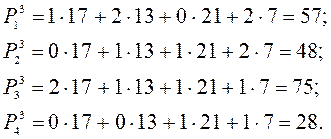
Коэффициенты относительной важности третьей итерации будут равны:
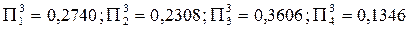 , а четвертой итерации -
, а четвертой итерации - 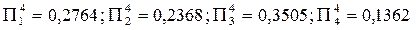 .
.
Можно непосредственно убедиться в том, что от итерации к итерации разности между значениями коэффициентов относительной важности становятся все меньше и меньше. Это не является случайным.
В алгебраической теории матриц доказывается, что для матрицы, составленной по формулам (3.1) и (3.2), вычисление коэффициентов по вышеприведенным правилам приводит в пределе при неограниченном увеличении числа итераций к нахождению одного из так называемых собственных векторов этой матрицы. Этот предел, вследствие теоремы Перрона – Фробениуса, всегда существует и его можно взять в качестве результирующего значения коэффициентов относительной важности критериев.
Нахождение коэффициентов относительной важности 1-й, 2-й и т.д. итераций можно формализовать, представив процесс вычислений в виде следующего алгоритма.
Шаг 1. Вычисляем коэффициенты относительной важности критериев первой итерации 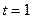 по формуле
по формуле
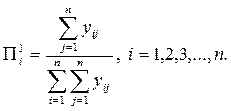
Шаг 2. Переходим к вычислению коэффициентов относительной важности следующей итерации, полагая 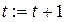 .
.
Шаг 3. Вычисляем коэффициенты относительной важности критериев итерации t по формуле
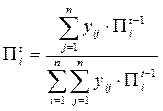 .
.
Шаг 4. Задаемся точностью вычислений 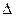 . Сравниваем значения
. Сравниваем значения 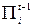 и
и 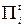
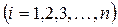 . Если
. Если 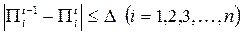 , то процесс вычислений заканчивается. В противном случае выполняем шаг 2.
, то процесс вычислений заканчивается. В противном случае выполняем шаг 2.
3.2.3. Определение степени согласованности мнений экспертов по количественным оценкам весовых коэффициентов относительной важности локальных критериев
Обозначим найденные в предыдущем разделе коэффициенты относительной важности для эксперта с номером m ( m =1,2,…, M ) через 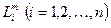 . Необходимо определить степень согласованности мнений этих экспертов.
. Необходимо определить степень согласованности мнений этих экспертов.
Одним из возможных подходов к определению степени согласованности мнений экспертов является подход, основанный на использовании метода ранговой корреляции и вычислении так называемого коэффициента конкордации W.
Для этого перейдем от значений коэффициентов относительной важности 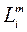 к рангам этих критериев
к рангам этих критериев 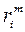 . При этом ранг, равный единице, присваивается критерию, у которого весовой коэффициент, соответствующий ему, наибольший.
. При этом ранг, равный единице, присваивается критерию, у которого весовой коэффициент, соответствующий ему, наибольший.
Ранги 1,2,3,…,n присваиваются критериям по мере уменьшения их весовых коэффициентов. Ранг n присваивается критерию, имеющему наименьший весовой коэффициент. Например, для рассматриваемого выше примера, полагая m =1, а в качестве значений 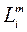 (i =1,2,3,4) соответствующие значения
(i =1,2,3,4) соответствующие значения 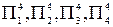 , получаем следующие значения рангов критериев:
, получаем следующие значения рангов критериев: 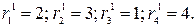 Таким образом, критерии расположатся в следующей последовательности с точки зрения убывания их важности:
Таким образом, критерии расположатся в следующей последовательности с точки зрения убывания их важности: 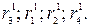
Коэффициент конкордации W рассчитывается по следующей формуле, предложенной Кендалом:
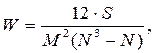 (3.3)
(3.3)
где
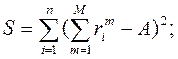 (3.4)
(3.4)
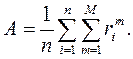 (3.5)
(3.5)
M – количество экспертов, m =1,2,…, M;
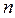 – количество локальных критериев,
– количество локальных критериев, 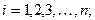
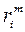 - ранг локального критерия с номером
- ранг локального критерия с номером 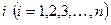 согласно мнению эксперта с номером m ( m =1,2,…, M ).
согласно мнению эксперта с номером m ( m =1,2,…, M ).
Коэффициент конкордации W меняется от 0 до 1, причем, если он равен 1, то оценки всех экспертов полностью совпадают; если же он равен 0, то связь между оценками отсутствует.
Если 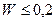 , то согласованность оценивается как низкая; если
, то согласованность оценивается как низкая; если 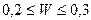 - удовлетворительная и если
- удовлетворительная и если 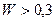 - высокая.
- высокая.
Низкий коэффициент согласованности указывает либо на неудачный выбор ранжируемых факторов, либо на то, что мнения экспертов по данному вопросу резко расходятся. В этом случае необходимо провести новый экспертный опрос, возможно изменив состав экспертов.
Рассмотрим следующий пример. Пусть в результате опроса трех экспертов были получены следующие итоговые результаты:
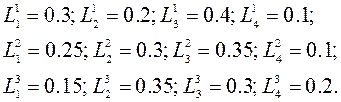
При этом ранги коэффициентов относительной важности для каждого из экспертов будут иметь следующие значения:
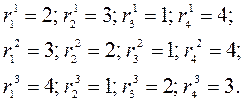
В данном примере M=3, N=4. Вычисляем вначале значение величины А по формуле (3.5):
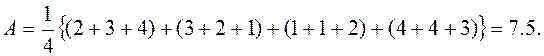
Вычисляем теперь значение величины S по формуле (4):
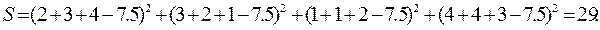
Вычисляем значение коэффициента конкордации W по формуле (3.3):
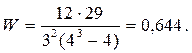
Достаточно высокий коэффициент конкордации свидетельствует о большой степени согласия экспертов.
Если гипотеза о согласии экспертов принимается, то вычисляются обобщенные итоговые значения весовых коэффициентов относительной важности критериев 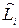 (i =1,2,…, N) по следующей формуле:
(i =1,2,…, N) по следующей формуле:
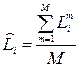 (3.6)
(3.6)
Для рассмотренного выше примера имеем следующий результат:
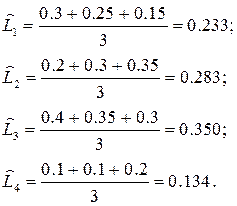
Формула (3.6) предполагает, что все эксперты по своему уровню равносильны, т.е. их мнение одинаково верно. Если это не так, то вместо формулы (3.6) следует применять формулу
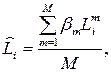 (3.7)
(3.7)
где 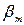 - коэффициент, отражающий степень авторитетности эксперта с номером m ( m =1,2,…, M ). Для определения коэффициентов
- коэффициент, отражающий степень авторитетности эксперта с номером m ( m =1,2,…, M ). Для определения коэффициентов 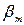 ( m =1,2,…, M ) можно применить ту же методику, что и для определения коэффициентов
( m =1,2,…, M ) можно применить ту же методику, что и для определения коэффициентов 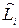 ( i =1,2,…, N ).
( i =1,2,…, N ).
3.3. Контрольные вопросы
1. Для чего необходимо определять количественные оценки предстоящих разработок?
2. Какова содержательная постановка задачи построения модели для вычисления количественной оценки предстоящей разработки?
3. Как строится таблица для проведения экспертного опроса специалистов?
4. Как формализуется и решается задача определения коэффициентов относительной важности параметров?
5. Почему необходимо переходить от значений коэффициентов относительной важности параметров к их рангам?
6. Что необходимо предпринять, если состав экспертов не однороден?