Последовательная структура. Очевидно, что .
Кольцевая структура. Очевидно, что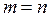 
.
Радиальная структура. Очевидно, что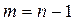 
.
Древовидная структура. Определить в общем случае трудно, так как этот параметр определяется видом дерева.
Структура в виде полного графа. В этом случае
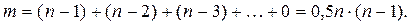
Несвязная структура эту характеристику не имеет.
2. Структурная избыточность. Этот структурный параметр отражает превышение общего числа связей над необходимым минимальным числом связей. Для вычисления этого параметра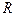 
можно применить следующую формулу:
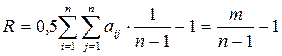. (1.2)
Найдем структурную избыточность для рассмотренных типовых структур, используя ранее найденную зависимость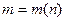 
.
Последовательная структура: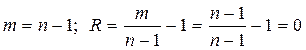 
.
Кольцевая структура: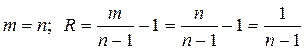 
.
Радиальная структура: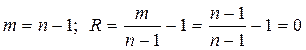 
.
Структура в виде полного графа: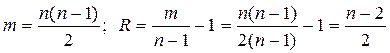 
.
Данная структурная характеристика используется для косвенной оценки экономичности и надежности исследуемой системы. Для систем с избыточностью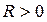 
, для систем с минимальной избыточностью 
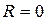, для несвязных систем 
.
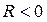Очевидно, что чем больше 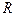, тем потенциально более надежна система. Но структурная избыточность может быть достигнута за счет увеличения связности только одних вершин. Поэтому вводят параметр 
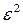, учитывающий неравномерность распределения связей или их несимметричность. Для этого введем понятие «степень вершины» 
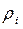, т.е. число ребер, инцидентных вершине с номером 
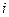. Нетрудно показать, что справедлива следующая формула: 
.
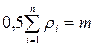Определим величину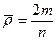 
, которую можно рассматривать как средняя степень вершины. В качестве параметра 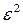можно теперь взять среднее квадратичное отклонение, т.е.
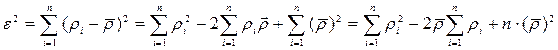. 1.3)
Так как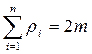 
и 
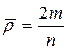, то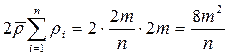 
. Кроме того, 
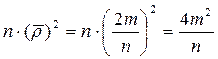. Подставив эти выражения в формулу (1.3), получим следующую формулу для вычисления параметра 
:
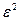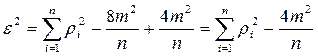. (1.4)
Параметр 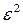характеризует недоиспользованные возможности заданной структуры, имеющей 
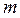ребер и 
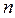вершин.
Определим структурную избыточность для рассмотренных типовых схем.
Для последовательной структуры имеем
, 
.
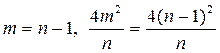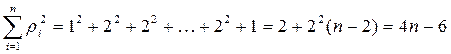Поэтому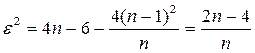 
.
Для кольцевой структуры имеем
.
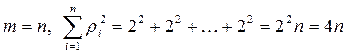Поэтому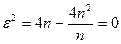 
.
Для радиальной структуры имеем
.
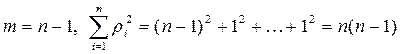Поэтому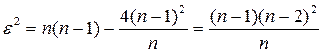 
.
Для структуры в виде полного графа имеем
,
.
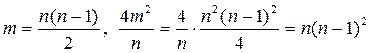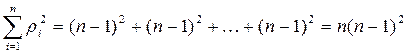Поэтому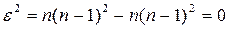 
.
3. Структурная компактность. Для ее оценки введем параметр, отображающий близость элементов между собой. Близость двух элементов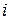 
и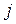 
определяется через минимальную длину пути для ориентированного графа (цепи – для неориентированного графа) - 
.
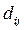Сумма всех минимальных путей (цепей) между всеми элементами отражает общую структурную близость элементов в анализируемой структуре. Обозначим эту величину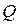 
и, в соответствии с определением, будем иметь
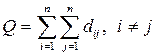. (1.5)
Рассмотрим вычислительные формулы для получения значений этого параметра для основных структур.
Последовательная структура:
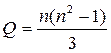. (1.6)
Кольцевая структура:
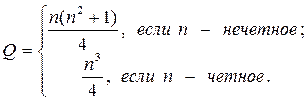(1.7)
Радиальная структура:
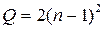. (1.8)
Структура в виде полного графа:
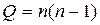. (1.9)
Для оценки структурной компактности часто используют относительный показатель
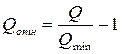, (1.10)
где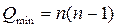 
- минимальное значение компактности для структуры типа полный граф.
Структурную компактность можно характеризовать и другим показателем – диаметром структуры:
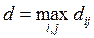. (1.11)
У полного графа указанная величина равна единице, поэтому он и обладает максимальной компактностью.
Учитывая преобладающий информационный характер связей в АСОИУ, можно сказать, что как величина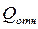 
, так и 
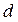интегрально оценивают инерционность процессов в системе, а при равных значениях 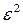и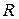 
(равномерность и структурная избыточность) их возрастание отражает увеличение числа разделяющих связей в структуре, характеризуя тем самым снижение общей надежности системы.
4. Степень централизации структуры. Для характеристики этого параметра можно воспользоваться следующим показателем:
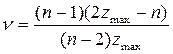, (1.12)
где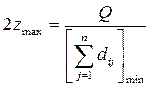 
.
Для структур с максимальной степенью централизации (радиальная)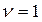 
, для структур с равномерным распределением связей (кольцевая и полный граф) 
.
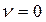Сравнительный анализ топологических структур, рассмотренных ранее, сведен в табл. 1.1.
Анализ табл. 1.1. показывает следующее.
1. Для несвязных структур структурная избыточность 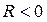, для структур без избыточности (последовательная, радиальная, древовидная) 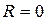; для структур с избыточностью по связям (кольцевая, полный граф) 
.
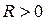2. Структуры (последовательная, радиальная, древовидная) с 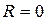различаются по показателю 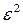, наибольшую неравномерность связей имеет радиальная структура.
Таблица 1.1
| Структура | Параметры | |||||
|
|
| 
|  
| 
| 
| |
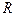
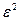
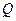
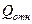
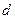
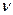
| Последовательная | 0 | 1,2 | 40 | 1,0 | 4 | 0,7 |
| Кольцевая | 0,25 | 0 | 30 | 0,5 | 2 | 0 |
| Радиальная | 0 | 7,2 | 32 | 0,6 | 2 | 1,0 |
| Древовидная | 0 | 3,2 | 36 | 0,8 | 3 | 0,81 |
| Полный граф | 2,5 | 0 | 20 | 0 | 1 | 0 |
| Несвязная | -0,25 | - | - | - | - | - |
3. Наибольшую близость элементов (показатель 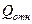) имеет структура типа полный граф, наименьшую — последовательная структура.
4. Радиальная и древовидная структуры, имеющие одинаковые или близкие значения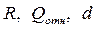 
значительно отличаются по показателям 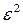и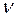 
, что соответствует физическому смыслу, так как отход от полной централизации в структуре ведет к большей равномерности распределения связей по элементам.
Рассмотрим следующий пример анализа структурно-топологических характеристик некоторой структуры.
Пусть дана структура, имеющая вид, показанный на рис. 1.5.
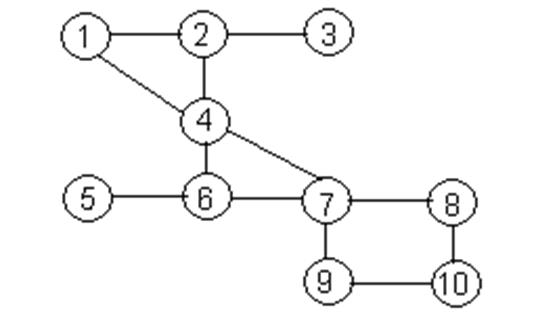
Рис. 1.5. Пример структуры
Вычислим все характеристики для данной структуры, а также для типовых структур, полагая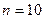 
. Результаты сведены в табл. 1.2
Таблица 1.2
| Структура | Параметры | |||||
|
|
|
|
|
|
| |
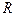
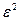
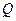
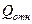
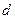
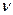
| Последовательная | 0 | 1,6 | 330 | 2,67 | 9 | 0,18 |
| Кольцевая | 0,1 | 0 | 250 | 1,78 | 2 | 0 |
| Радиальная | 0 | 57,6 | 162 | 0,8 | 2 | 1,0 |
| Древовидная | 0,33 | 7,6 | 257 | 1,85 | 5 | 0,76 |
| Полный граф | 4 | 0 | 90 | 0 | 1 | 0 |
| Анализируемая структура | 0,33 | 10,4 | 210 | 1,3 | 5 | 0,643 |
Из анализа табл. 1.2. следует, что по своим параметрам анализируемая структура ближе всего к древовидной структуре.
Если заранее изучить свойства типовых структур, то можно с большой долей уверенности судить о свойствах анализируемой структуры по близости соответствующих параметров.
1.4. Контрольные вопросы
1. Что является исходными данными для решения задач проектирования организационной структуры проектируемой АСОИУ?
2. По какому критерию выбирается оптимальный вариант организационной структуры проектируемой АСОИУ?
3. Как строится исходная организационная структура системы управления исследуемого объекта автоматизации?
4. В чем содержательный смысл матрицы циклических соединений?
5. По какому принципу корректируется исходная матрица организационной структуры?
6. Как строится матрица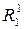 
?
7. Почему следует применять числовые характеристики полученной организационной структуры АСОИУ.