Осевые инварианты выполняют функцию поддержания движения оси симметрии, ориентированного в сторону роста размерности потока пространства—времени.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Представим таблицу величин, ориентирующих ось симметрии во времени.

Уровни оси симметрии	Размерность направляющего вектора во времени	Имя величины
Уровень 1		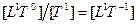Скорость
Уровень 2		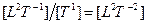Разность потенциалов
Уровень 3		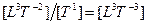Ток. Массовый расход
Уровень 4		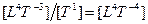Сила
Уровень 5		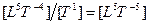Мощность
Уровень 6		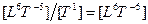Скорость передачи мощности

Каждый осевой инвариант есть ортогональное пересечение Времени и Пространства одинаковой размерности. В силу этого они поддерживают ось симметрии в равновесии на каждом ее уровне. Однако между уровнями имеет место неравновесие пространственно-временных потоков. Все пространственно-ориентированные потоки являются неравновесными: 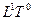, , 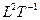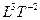и т.д.

Но именно эти потоки и обеспечивают переходы между осевыми инвариантами, т.е. переходы от замкнутых равновесных процессов к открытым неравновесным. Рассмотрим эти вопросы. Поддержание оси симметрии в равновесии обеспечивается симметрично инверсными свойствами осевых инвариантов. Каждый такой инвариант является одновременно стоком и истоком потоков, т.е. осциллятором. В силу этого образуются ортогональные замкнутые пространства L—T, симметрично расположенные по обе стороны оси симметрии.

Ось

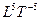
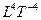
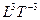
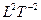
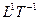
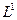
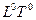
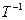
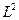
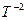
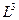
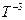
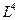
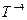
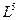
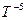
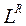
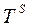
Замкнутые пространства являются частным случаем открытых. Замкнутость имеет место в ситуации, когда направляющие в пространстве вектора являются константами. В этом случае осевые инварианты равны нулю, и структура становится замкнутой. Например, если 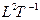= const, то 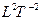= 0, или если 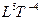= const, то 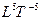= 0.

Однако инварианты имеют свои группы преобразований. эти группы образуются разложением инварианта в степенной ряд. Каждый член ряда является потенциальным источником нарушения замкнутости, так как увеличивает частоту колебаний и тем самым способствует тому, чтобы направляющие в пространстве вектора не были константами.

Как было показано ранее, процесс взаимодействия пространственно-временных потоков имеет ярко выраженный торообразный циклический характер. От 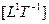до 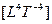протекает единый цикл формирования четырехмерного пространственно-временного тора*. Начиная с 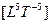и до 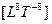, протекает второй торообразный цикл и так далее. Весь процесс взаимодействия L « T представляет цепь, звеньями которой выступают торы, «нанизанные» на ось симметрии .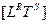