7. 7. Генератором времени является инвариант с допустимыми группами преобразований.
8. 8. Спектр пространственных мер
Рассмотрим теперь ортогональный ряд, где величина А находится в зависимости от изменения размерности пространства [L], а размерность времени «заморожена».
,
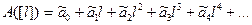где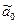 
— начальное положение 
;
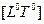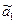= 0, сдвиг отрезка 
;
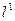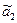= 0, сдвиг площади 
;
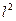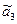= 0, сдвиг объема 
;
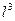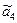= 0, сдвиг тора 
.
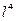Здесь также появляются новые качества, но они связаны со спектром геометрических мер.
| Геометрические меры |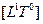 
отрезок
| 
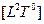площадь
| 
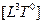объем
| 
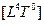тор
| 
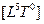гипертор
|
Однако, здесь будет уместно спросить: «Каким образом эти пространственные объекты связаны между собой?». Оказывается, чтобы на этот вопрос ответить, нельзя обойтись без времени. Время порождает пространство и, наоборот. Рассмотрим вначале связь одномерной длины 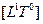с одномерным временем 
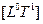и покажем как формируется размерность Пространства и Времени.
9. 9. Связь пространственных и временных мер
Второй парой предикатов, с логической необходимостью вытекающей из первой пары предикатов «идеальной точки» являются также два фундаментальных понятия:
· · 
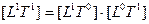— длительность расстояния;
· · 
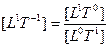— скорость.
Связь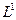 
с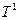 
есть длительность расстояния 
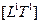, определяемая «площадью поверхности, пройденной с определенной скоростью»:
, .
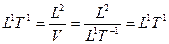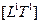Длительность расстояния и скорость определяют алгоритм формирования размерности Пространства и Времени любой целочисленной мерности.
При этом четномерные пространства определяются по формуле:
,
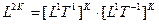где 2K — размерность пространства;
K — целые положительные числа.
Например: двухмерное пространство: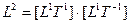 
;
четырехмерное пространство: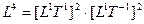 
.
Нечетномерные пространства:
.
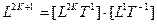Например: трехмерное пространство: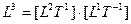 
;
пятимерное пространство: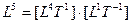 
.
Размерность Времени определяется как отношение длительности расстояния к скорости, с соответствующей мерностью Времени:
.
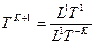Например: двухмерное время: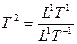 
;
трехмерное время: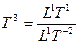 
;
пятимерное время: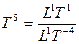 
.
Разделение Пространства на четно- и нечетномерные обусловлено особенностью проективных пространств, связанной с механизмом работы Универсума, а точнее с его механизмом замкнутости—открытости.
10. 10. Алгоритм взаимодействия Времени и Пространства
Его суть заключается в том, что для сохранения, то есть для поддержания, Универсума в процессе взаимодействия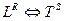 
формируется ось симметрии, на которой располагаются симметрично инверсные 
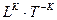— «осевые» инварианты, то есть имеющие одинаковую размерность, но разный знак.
Очевидно, что все «осевые» инварианты различаются по скоростям и обеспечивают ее сохранение в границах своей размерности. При этом их размерность в зависимости от скорости может быть определена отношением размерности пространства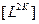 
к размерности длительности этого пространства: 
.
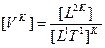11. 11. Ось симметрии как скоростной канал
Ось симметрии выполняет функцию скоростного канала. Он обладает определенной пропускной способностью в зависимости от скоростных свойств осевых инвариантов. Канал может закрываться и открываться в зависимости от свойств преобразуемых пространственно-временных потоков.
Подобно тому, как растет ствол обычного дерева, растет и ось симметрии, но этот рост, в отличие от дерева, проявляется в «наращивании» размерности инвариантов при переходе от одной скорости протекания LT-потоков к другой.
Это «наращивание» протекает в процессе чередования четно- и нечетномерных пространств и имеет определенную цикличность. Один цикл равен четырем мерностям LT и протекает от одномерного до четырехмерного LT. Начиная с пятой размерности цикл повторяется, но на «возросшей» оси симметрии.
Они располагаются по уровням в порядке возрастания размерности «осевых» инвариантов:
Уровень 1: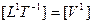 
= скорость;
Уровень 2: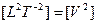 
= разность потенциалов;
Уровень 3: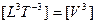 
= ток;
Уровень 4: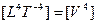 
= сила;
Уровень 5: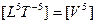 
= мощность;
Уровень 6: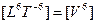 
= мобильность.
В графическом варианте это выглядит так:
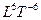
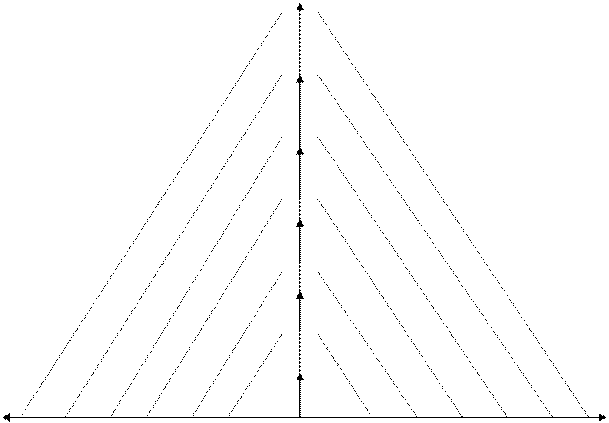
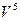
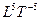
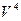
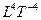
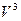
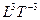
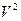
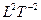
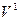
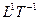
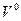
L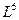 
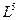
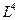
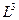
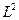
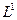
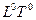
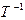
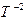
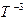
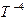
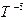
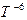T
12. 12. Алгоритм формирования направления движения
Рассмотрим алгоритм формирования направляющего вектора скорости оси симметрии. Его суть в двухтактном переходе от одного осевого инварианта к другому с возрастающими скоростными качествами. На первом такте формируется направляющий вектор в пространстве, а на втором — направляющий вектор во Времени. Их отношение определяет направляющий вектор скорости на каждом уровне оси симметрии. Рассмотрим этот алгоритм.
Каждый осевой инвариант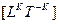 
может быть представлен как произведение ориентированной скорости 
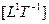на размерность величины предыдущего уровня.
.
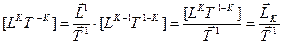Это означает, что направляющим вектором в пространстве для K-го осевого инварианта является величина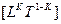 
. Представим список ориентирующих в пространстве величин для каждого уровня симметрии.
| Уровни оси симметрии | Размерность направляющего вектора в пространстве | Имя величины |
| Уровень 1 |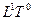 
| Длина (одномерная) |
| Уровень 2 |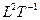 
| Двумерная поверхность с угловой скоростью |
| Уровень 3 |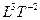 
| Масса, заряд |
| Уровень 4 |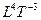 
| Скорость смещения заряда, импульс |
| Уровень 5 |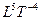 
| Энергия |
| Уровень 6 |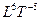 
| Скорость передачи энергии |