Система в целом — это, прежде всего, полная система универсальных понятий отображающих сущность систем реального мира.
Она является бесконечной. Это означает, что не существует ограничений на количество величин-понятий. В ходе развития научной мысли их список будет все время пополняться.
10. Иерархия величин
Система представляет иерархию вложенных понятий. Величина, являющаяся сущностью одного класса систем, может быть явлением-проекцией другого нижележащего класса систем. На данное время в вершине этой иерархии находятся понятия: мощность и мобильность (скорость переноса мощности). Другие величины имеют меньшую пространственно-временную размерность и поэтому могут быть выведены. Покажем это на примере величин, у которых размерность длины и времени одинаковые, но с разным знаком. Эти величины пересекают всю таблицу (см. рис. 3.1) по диагонали, разделяя ее на две части и образуя группу симметрично-инверсных, или «осевых», величин:
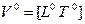 — константа;
— константа;
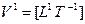 — скорость;
— скорость;
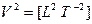 — разность потенциалов;
— разность потенциалов;
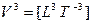 — ток;
— ток;
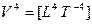 — сила;
— сила;
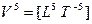 — мощность.
— мощность.
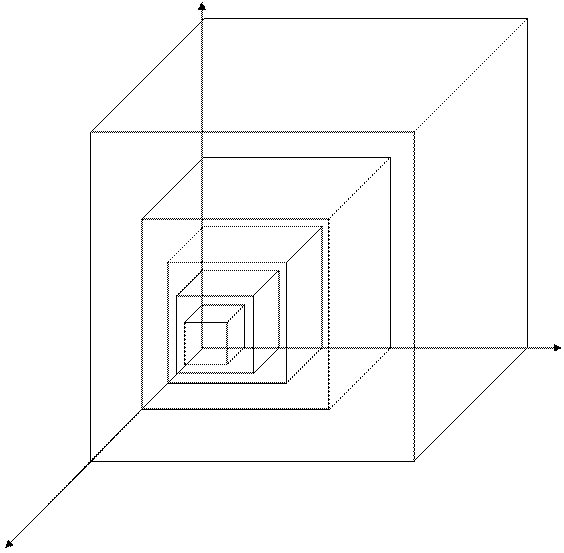
Все представленные величины различаются по скоростям и являются вложенными одна в другую, образуя полиэдральный куб (рис. 3.2).
5
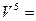 мощность
мощность
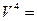 сила
сила
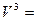 ток
ток
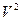
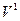
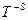
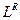
Рис. 3.2
Здесь наглядно видно, что величиной, объединяющей всю группу, является мощность. Все другие симметрично-инверсные величины являются составными элементами мощности и могут быть через нее выражены. В этом смысле мощность является наиболее общей величиной. Закон сохранения мощности имеет наибольшую силу, охватывая наиболее широкий класс систем. В классических консервативных системах требуется постоянство скорости. Это требование снимается при работе с инвариантом мощности.
В дальнейшем изложении это утверждение будет предметом специального рассмотрения.
11. Энергия и мощность
В системе 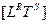 энергия имеет размерность
энергия имеет размерность 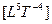 , а мощность —
, а мощность — 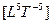 .
.
Основным свойством энергии является ее способность совершать работу в процессе превращения из одной формы в другую.
Основным свойством мощности является работоспособность в единицу времени.
По этой причине полная энергия Е произвольной системы является суммой двух частей:
1) 1) превратимой, или свободной, энергии В,
2) 2) непревратимой, или связной, энергии А (при данных природных и технологических условиях)
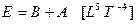 . (3.2)
. (3.2)
12. Свободная и связная энергия
Если полное максимальное значение энергии системы обозначить Emax, а минимальное значение энергии — Emin, тогда мы получаем еще одно значение энергии, которое есть разность между максимальным и минимальным значением энергии — это «свободная энергия» В:
В = Eсвоб = Emax - Emin. (3.3)
Мы можем записать
Emax = Eсвоб + Emin. (3.4)
Минимальное значение энергии Emin называется «связной энергией» А. Обозначая «связную энергию» º «минимальной энергии» А = Eсвяз , получим
Emax = Eсвоб + Eсвяз , или Emax = В + А. (3.5)
Очевидно, что Emax в классической термодинамике называется полной энергией системы.
«Одномерное» пространство можно изображать в виде «отрезка», состоящего из двух компонент: «свободной» энергии и «связной» энергии. Изобразим это на рис. 3.3.
1 А 2 В 3
|
|
| ||||
| Eсвяз | Eсвоб | ||||
|
| «свободная» энергия Eполн | ||||
| полная энергия | |||||
Рис. 3.3. Одномерное фазовое пространство энергии
Очевидно, что на этой диаграмме любое состояние системы представляется точкой 2, которая лежит МЕЖДУ точкой 1 и точкой 3.
В зависимости от значения «свободной» и «связной» энергии состояние системы изменяется, что проявляется в перемещении «точки 2». При увеличении «свободной» энергии точка перемещается влево, а при увеличении «связной» энергии — вправо.
Состояние системы может быть определено по соотношению «свободной» и «связной» энергий. Понятно, что чем больше значение «свободной» энергии, тем выше работоспособность системы. Поэтому отношение «свободной» энергии к полной энергии определяет коэффициент полезного действия (КПД) системы:
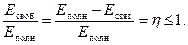 (3.6)
(3.6)
Очевидно, что КПД системы достигает значения 1, когда «связная» энергия обращается в нуль, и, наоборот, — КПД системы достигает значения близкого к нулю, когда связная энергия приближается к значению полной энергии системы.
Поэтому очень важно правильно определить «полную», «свободную» и «связную» энергии системы.
Естественно в этой связи обратиться к термодинамике, где и было введено понятие термодинамического коэффициента полезного действия для паровых машин, когда появился цикл Карно. Впоследствии в уравнениях Гельмгольца и Гиббса была показана связь «полной», «свободной» и «связной» энергий для изотермически замкнутых систем. В уравнениях Гельмгольца эта связь выглядит следующим образом:
Eполн = Eсвоб + T × S. (3.7)
Здесь «связная» энергия представляется произведением температуры Т термометрического тела и энтропии S изолированной системы.
Однако, нетрудно убедиться в том, что понятия «температура» и «энтропия» в пространственно-временной системе 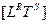 отсутствуют. Это обстоятельство вынуждает нас рассмотреть эти понятия внимательней.
отсутствуют. Это обстоятельство вынуждает нас рассмотреть эти понятия внимательней.
13. Температура и энтропия
Для определения связной энергии нужно измерять энтропию и температуру. Но что это такое?
Мы хотели бы обратить внимание на одну «физическую константу», известную как константа Больцмана. Константа Больцмана k = 1,38054 ´ 10-16 эрг×град-1 фигурирует в физике, как «постоянная» и связывает классическую термодинамику со статистической физикой, как в классическом случае, так и в квантовой механике. Действительно ли это «физическая постоянная»? Нетрудно доказать, что это не так.
Известно, что в школьной физике, да и в учебниках высшей школы, фигурирует формула:
E = pV = RT. (3.8)
Здесь E — энергия, накопленная в форме тепла в газе, p — давление газа, V — объем газа, R — газовая постоянная, T — температура газа.
Вообще говоря, такую зависимость теоретическая физика имеет только для «идеального газа».
Через некоторое время, когда было обнаружено, что теплоемкость газов различна и зависит от числа степеней свободы (которые считались определяемыми числом атомов в молекуле), было принято соглашение относить постоянную R не к одному молю газа, а относить на одну «степень свободы» молекулы — это соглашение превратило «газовую постоянную» в «константу Больцмана». Эта последняя выражается отношением газовой постоянной к числу молекул в грамм-молекуле.
k = R : N = 1,38054 ´ 10-16 эрг×град-1. (3.9)
Некоторое время спустя эту константу начали умножать на множитель, зависящий от сложности молекул, используя представление о степенях свободы. Формула (3.8) приобретает вид:
E = pV = nkNT, (3.10)
где E — энергия газа, p — давление газа, V — объем газа, kN = R — газовая постоянная, n — множитель, учитывающий число степеней свободы и принимающий значения: 3/2, 5/2, 7/2, … Через некоторое время спустя снова пришлось корректировать формулу теплоемкости газа, которая оказалась сама зависящей от температуры. Традиционный математический прием аппроксимации изменяющейся величины — это разложение в ряд по степеням независимой переменной. Возвращаясь снова к газовой постоянной (разложение в степенной ряд лишает эту величину статуса постоянной — теперь она переменная, представляемая суммой ряда) запишем разложение в ряд по степеням температуры:
E = pV = (R0 + R1T + R2T2 + R3T3 + …)T. (3.11)
Мы получили новый вид функции, выражающий ИЗМЕНЕНИЕ теплоемкости газа в зависимости от температуры, то есть установили, что газовая «постоянная» НЕ ЯВЛЯЕТСЯ «ПОСТОЯННОЙ», а что эта величина изменяется с изменением температуры. Формула (3.11) имеет очень громоздкий вид. Для уменьшения числа членов в степенном ряду можно заменить этот ряд некоторой новой буквой, заменяющей этот ряд. Выбираем для этого обозначения букву S. Имеем:
S = R0 + R1T + R2T2 + R3T3 + … (3.12)
Подставляем это значение в формулу (3.11), но не будем забывать, что скрывается за символом S:
E = pV = ST. (3.13)
Сравним формулу (3.13) с формулой (3.8) и зададимся вопросом: «На какой же формуле базируется статистическая физика?»
Ведь нельзя ПОСТУЛИРОВАТЬ в рамках одной и той же теории в качестве ИСТИННЫХ — ДВЕ различные формулы для одной и той же энергии газа.
Физик сразу же поймет, что буква S выбрана не случайно — да, это и есть ЭНТРОПИЯ. Нетрудно убедиться в этом, записывая выражение для «свободной энергии»:
F = pV - ST. (3.14)
Дифференцируя это выражение, мы получим хорошо известную формулу изменения свободной энергии:
dF = p dV + V dp - S dT - T dS. (3.15)
Интеграл от этого полного дифференциала возвращает нас к формулам (3.14) и (3.13). Для начала заметим, что для равновесных систем свободная энергия равна нулю. С другой стороны, обращаясь к формуле (3.11) и к формуле (3.13), зададимся не традиционным вопросом: «Что такое ЭНТРОПИЯ?», а вопросом: «Что мы измеряем, когда измеряем температуру?» Ведь измерение температуры задавалось правилом, что при постоянном давлении между температурой и объемом термометрического тела существует ЛИНЕЙНАЯ ЗАВИСИМОСТЬ, которая и выражается ГАЗОВОЙ ПОСТОЯННОЙ. ЭТО означает, что приращение энергии газа выражается через приращение температуры.
Небольшое размышление показывает, что исторически термин температура связан с изменением объема термометрического тела и ПРЕДПОЛОЖЕНИЕМ О ЛИНЕЙНОЙ ЗАВИСИМОСТИ ЭНЕРГИИ ТЕЛА ОТ ЕГО ОБЪЕМА. В этом случае в формуле (3.8) приращение энергии можно выразить через приращение объема, то есть:
dE = R dV. (3.16)
Здесь мы показываем, что измеряемой физической величиной, которую измеряла классическая физика и называла ТЕМПЕРАТУРОЙ, была величина изменения ОБЪЕМА термометрического тела, что мы делаем и в наши дни при использовании термометров расширения.
Обратимся к формуле (3.13) — здесь та же ситуация, только вместо буквы R стоит буква S. Но физический смысл остается без изменения — эта переменная величина связывает между собою энергию и объем термометрического тела. Имеем:
dE = S dV. (3.17)
При обсуждении парадоксального положения, связанного с использованием в основаниях статистической физики ДВУХ ВЗАИМОИСКЛЮЧАЮЩИХ ФОРМУЛ, приходилось слышать, что величина S существенно ПОЛОЖИТЕЛЬНА. И это положение не выдерживает критики: достаточно заполнить термометр расширения водой и нагревать от 0 до 40° по Цельсию, чтобы получить положительную величину прироста энергии (при уменьшающемся объеме) необходимо считать значение S отрицательным.
Еще в 1961 г. в одной из своих публикаций были показаны абсолютные отрицательные температуры при фазовых переходах, в окислительно-восстановительном потенциале и при фотохимических реакциях.
Вообще, абсолютные отрицательные температуры появляются там, где возможно устойчивое существование микрочастиц на верхнем и нижнем энергетических уровнях — например, фазовый переход и окислительно-восстановительный потенциал (железо-3 — более высокий энергетический уровень, чем железо-2). Фотосинтез: продукты фотосинтеза занимают более высокий энергетический уровень, чем исходные вещества.
Известна работа Э.Шредингера: «Что такое жизнь с точки зрения физики?». В ней Шредингер делает заявление, что растение питается «отрицательной энтропией». Проверка этого утверждения прямым расчетом показала, что Шредингер прав тогда и только тогда, когда температура листа растения имеет абсолютное отрицательное значение. Таким образом, «отрицательная энтропия» имеет ту же природу, что и абсолютные отрицательные температуры.
Вообще говоря, этот вывод хорошо объясняет, почему С.Подолинский, Э.Бауэр, В.Вернадский, а впоследствии и многие другие крупные ученые, для определения физических основ явлений жизни не стали обращаться к понятию ЭНТРОПИЯ, а использовали понятие «свободная энергия».
Мы вновь возвращаемся к этому понятию и хотим показать связь свободной энергии с другими видами энергии.
14. Связь свободной энергии с потенциальной и кинетической
Для установления связи мы будем использовать фазовые диаграммы, которые принято использовать при анализе работы различных машин. Мы можем показать эту связь на примере любого типа машин: механических, термодинамических, электрических, электромагнитных и др. Для простоты изложения воспользуемся обычным маятником (рис. 3.4).
Полная энергия маятника, состоящего из «пружины» и «массы» тела, будет при отсутствии «диссипативных» сил постоянна и состоять из «кинетической» и «потенциальной» энергии и еще какой-то «связной» энергии.

-F +F
Рис. 3.4. Обычный маятник
Наш «маятник» состоит из массы (размещен на тележке, которая катается без трения) и соединен с пружиной, которая обладает жесткостью K. В начальном положении сила натяжения-сжатия пружины равна нулю. Оттянем пружину до некоторой отметки на оси F, т.е. сообщим системе некоторое количество энергии, которое и будет «свободной» энергией. Отпустим тележку — она начнет совершать гармоническое колебание около положения равновесия. Общая и свободная энергия (из-за отсутствия диссипации) будут сохраняться, а «потенциальная» и «кинетическая» энергия будут переходить друг в друга. При этих взаимных переходах представляющая точка D будет перемещаться на отрезке 1—3.
Теперь мы должны «отождествить» наши точки 2 и 3 с точкой D; будем считать, что точка D находится в точке B, когда свободная энергия является «потенциальной» энергией; когда точка D находится в точке 3, то вся свободная энергия является «кинетической». Считая «кинетическую» и «потенциальную» энергию «компонентами» свободной энергии, мы можем рассматривать свободную энергию как векторную сумму своих компонент. Поскольку угол между кинетической и потенциальной энергией — прямой, а свободная энергия — постоянна — инвариант, то представляющая точка D будет описывать окружность (рис. 3.5).
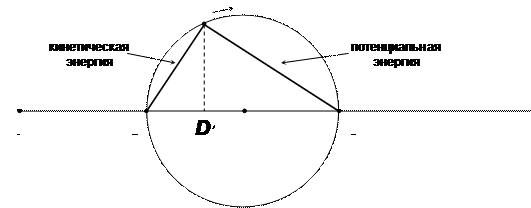
Рис. 3.5. «Гармоническое колебание» обычного маятника
Когда точка D находится в точке 2 — вся свободная энергия находится в форме потенциальной энергии. Когда D проходит через центр окружности, мы имеем равенство кинетической и потенциальной энергии. Приход в точку 3 соответствует пробеганию тележки с максимальной скоростью через нейтральное положение пружины — вся свободная энергия представлена в форме кинетической энергии. При движении по нижней полуокружности точки D происходит сжатие пружины. В точке 2 вся свободная энергия в потенциальной форме сжатия пружины. Следующий оборот точки D возвращает систему в исходное состояние.









 «связная» энергия
«связная» энергия