2. 2. Именем исходной системы координат.
3. 3. Именем «желательной» или «конечной» системы координат.
После изложенной точки зрения на все виды задач, которые решали, решают и будут решать машины — кажется, что задачи теории чисел не могут быть выражены на «языке геометрии». Это неверно. Первый пример использования геометрических образов в решении задач теории чисел продемонстрировал еще Гаусс. Об этом можно прочитать у Ф.Клейна в «Лекциях о развитии математики в XIX столетии», часть 1, с. 64—65.
13. Точечное преобразование и преобразование координат
Даны ДВА ВИДА ПРЕОБРАЗОВАHИЙ:
1. 1. Преобразование КООРДИHАТ.
2. 2. «ТОЧЕЧHОЕ» преобразование.
Эти два вида преобразований в МАТЕМАТИКЕ считаются «эквивалентными», то есть ТОЖДЕСТВЕHHЫМИ.
В преобразовании КООРДИHАТ мы имеем дело с ОДHОЙ И ТОЙ ЖЕ «ТОЧКОЙ», а в «ТОЧЕЧHОМ» преобразовании мы имеем дело с ОДHОЙ И ТОЙ ЖЕ «СИСТЕМОЙ КООРДИHАТ». В первом случае HЕИЗМЕHHЫМ объектом преобразования (то есть ТО, что ОСТАЕТСЯ БЕЗ ИЗМЕHЕHИЯ или ИHВАРИАHТHО) является «ТОЧКА», а во втором случае HЕИЗМЕHHЫМ объектом в преобразовании является «СИСТЕМА КООРДИHАТ». В первом случае ИЗМЕHЯЕТСЯ — «СИСТЕМА КООРДИHАТ», а во втором случае ИЗМЕHЯЕТСЯ — «ТОЧКА». Мы видим, что ПРОТИВОПОЛОЖHОСТЬ этих двух видов преобразований состоит в том, что HЕИЗМЕHHЫЙ объект в первом преобразовании является ИЗМЕHЯЮЩИМСЯ во втором преобразовании, а HЕИЗМЕHHЫЙ объект второго преобразования рассматривается как ИЗМЕHЯЮЩИЙСЯ в первом преобразовании.
Мы вполне согласны с математиками, что эти ДВЕ ТОЧКИ ЗРЕHИЯ на преобразование МАТЕМАТИЧЕСКИ ЭКВИВАЛЕHТHЫ, но мы не можем сказать, что эта эквивалентность математическая сохраняется, когда мы переходим к ПРИЛОЖЕHИЯМ МАТЕМАТИКИ, т.е. К ФИЗИЧЕСКОЙ РЕАЛЬHОСТИ.
14. Инварианты, системы координат и «точки зрения»
При описании физической реальности нам приходится искать в явлениях природы как раз то, что не зависит от ТОЧКИ ЗРЕHИЯ исследователя, т.е. ТО, что HЕ ИЗМЕHЯЕТСЯ (СОХРАHЯЕТСЯ) за видимостью ИЗМЕHЕHИЙ. Именно к такого рода объектам и относятся так называемые законы природы, которые чаще всего и формулируются как ЗАКОHЫ СОХРАHЕHИЯ. Историческая традиция математической физики как раз и состоит в том, что сохраняющийся в явлениях природы ОБЪЕКТ — отождествляется с тем или иным ГЕОМЕТРИЧЕСКИМ ОБЪЕКТОМ, а ПРОЯВЛЕHИЯ этого закона, наблюдаемого различными наблюдателями отождествляются с частными «системами координат», характеризующими особенности условий наблюдения того же самого ЗАКОHА.
Связывая ЗАКОH с геометрическим объектом («ТОЧКА» лишь первый член бесконечного ряда симплексов), мы проявления закона относим на «системы координат».
Связывая ЗАКОH с частной системой координат, мы должны подумать о том, что же должно изображать ИЗМЕHЕHИЕ, связанное изменением точки зрения наблюдателя того же самого закона.
15. Ум — измерение — наука
Здесь нам предстоит вернуться назад на половину тысячелетия. Только к середине пятнадцатого века само понятие «НАУКА» было связано с понятием «ИЗМЕРЕНИЕ», что и было совершено Николаем Кузанским. Последний, завершая эпоху схоластики, отождествлял УМ (по латыни — mens) с понятием ИЗМЕРЕНИЕ (по латыни — mensurare). В этом смысле «умный» — это человек «измеряющий». Проблема СООТНЕСЕНИЯ символов математических теорий с показаниями физических приборов — и есть проблема УМЕНИЯ использовать математику в решении прикладных проблем.
Подобно тому, как в приведенных выше формулах, мы встречали различное понимание «математических единиц», подобным образом и в реальном мире мы встречаемся с колоссальным разнообразием ФИЗИЧЕСКИХ ЕДИНИЦ. Проблема соотнесения математических и физических единиц и есть тот узел, который решается ДИАЛЕКТИКОЙ.
Уже двести лет тому назад, не без участия Канта, были сформулированы основные ЭСТЕТИЧЕСКИЕ понятия: чувственное восприятие ДЛИТЕЛЬНОСТИ и чувственное восприятие ПРОТЯЖЕННОСТИ. Мы встречаемся с этими понятиями под названием либо ПРОСТРАНСТВА, либо ВРЕМЕНИ. И здесь мы встречаемся со «злым гением» Минковского. Это с его легкой руки начали считать ПРОТЯЖЕННОСТЬ и ДЛИТЕЛЬНОСТЬ одним и тем же. Если просто помнить, что комплексное сопряжение означает поворот на угол в 90°, то можно понять, что ВРЕМЯ может считаться «ортогональным» к пространственной ПРОТЯЖЕННОСТИ. Мы уже имели исторический опыт Гамильтона, который (следуя Канту) хотел рассматривать алгебру, как НАУКУ О ЧИСТОМ ВРЕМЕНИ, считая ее дополнением к учению о ПРОСТРАНСТВЕ, изучаемому ГЕОМЕТРИЕЙ.
16. Геометрия и хронометрия
Именно здесь мы можем ПРОТИВОПОСТАВИТЬ как противоположенные два понятия: ГЕОМЕТРИЮ и ХРОНОМЕТРИЮ. Для сохранения исторической преемственности с классической математикой мы будем отождествлять ХРОНОМЕТРИЮ с ГОНИОМЕТРИЕЙ, следуя в этом пункте предложениям Ф.Клейна.
Обратим внимание на РАЗЛИЧИЕ их ЕДИНИЦ. Классическое различие единиц длины, площади и объема мы выражаем СТЕПЕНЯМИ (лучше говорить о СТУПЕНЯХ). Совсем иначе обстоит дело с единицами ВРЕМЕНИ. Основная единица ВРЕМЕНИ дается выражением (через углы) по Эйлеру.
17. Единицы измерения пространства и времени
Соотношение между пространственными единицами и единицами времени есть соотношение между АДДИТИВНОЙ и МУЛЬТИПЛИКАТИВНОЙ группами: сложению ДЛИН соответствует мультипликативное «сложение» УГЛОВ.
Принято считать, что первым обобщением понятия «число» был переход от действительных чисел к комплексным числам. Это неверно, хотя и закреплено исторической традицией. Давно известно, что комплексные числа можно представлять в виде спиноров в матричной форме. Но это не только ФОРМА: разве можно такое понятие как УГОЛ, образуемый пересечением ДВУХ ПРЯМЫХ, обозначить ОДНИМ числом, если уже обычную прямую аналитической геометрии мы не можем представить ОДНИМ числом? Заметим, что РАССТОЯНИЕ в геометрии является всегда ПОЛОЖИТЕЛЬНЫМ, в то же время измерение ДЛИТЕЛЬНОСТИ всегда предполагает ОРИЕНТАЦИЮ, которая отличает ПРОШЛОЕ ВРЕМЯ от БУДУЩЕГО ВРЕМЕНИ. Именно это различие ДЛИТЕЛЬНОСТИ и являет себя как математический термин «ПОРЯДОК». Этот термин невозможно определить с помощью читаемого ТЕКСТА, так как чтение текста ПРЕДПОЛАГАЕТ наличие знания в каком «ПОРЯДКЕ» следуют друг за другом как буквы, так и слова, определяющие сам термин «ПОРЯДОК».
Именно в этом смысле матричное представление УГЛА — есть минимальное обобщение понятия число. При матричном представлении углов совершенно очевидно, что СЛОЖЕНИЕ углов мы представляем как ПРОИЗВЕДЕНИЕ соответствующих матриц. Связь между сложением и умножением достигается с помощью логарифмического преобразования, что и приводит как к метрике Кэли, так и к метрике Лобачевского. Корректная «метризация» проективного пространства через углы дает нам связь алгебраических и трансцендентных функций.
Не является предметом данной работы излагать все дерево теорем, лемм и следствий, которое растет на фундаменте ОСНОВАНИЙ МАТЕМАТИКИ.
Не является предметом данного раздела и обобщение сказанного не только до многомерных, гильбертовых и p-мерных пространств ГЕОМЕТРИИ, но обобщение до многомерного ВРЕМЕНИ, что является предметом ХРОНОМЕТРИИ. Предложение О.Веблена по обобщению Эрлангенской программы Клейна, отвергнутое в Болонье, позволяет совершить переход от гармонического отношения четырех точек проективного пространства к гармоническому отношению ЧЕТЫРЕХ УГЛОВ на проективной плоскости. Этот шаг связывает в одно целое как геометрии Клейна, так и геометрии Римана. Совершенно очевидно, что при дальнейшем развитии, мы будем иметь дело не только с «плоскими», но и многомерными углами.
Понятие «многомерное время» не есть фантом пустого воображения. Социально-экономические системы имеют МЕРУ в форме общественно-необходимого времени на удовлетворение ВСЕХ потребностей. Обратим внимание, что количество названных нами «частных» времен равно количеству «частных» удовлетворяемых потребностей. Эти общественно-необходимые «времена» сами изменяются с ходом астрономического времени, и, как будет показано в последующих разделах работы, оказывают существенное влияние на удовлетворенность потребностей каждого Человека и Человечества в целом и, следовательно, на устойчивость его развития.
18. Какова «ключевая идея», которая приблизила нас
к современному уровню понимания математики?
Мы формулируем эту ИДЕЮ, как идею введения КООРДИHАТHЫХ СИСТЕМ. Без введения координатных систем мы по-прежнему баловались бы рисунками геометров Греции и не смогли бы УВИДЕТЬ ЕДИHСТВА ВСЕЙ МАТЕМАТИКИ: теперь мы можем все геометрические образы обсуждать на различных языках математики — на языке анализа, на языке алгебры, на языке топологии и т.д. Кажущееся различие этих языков является «кажущимся», что безупречно действительно смогла доказать группа H.Бурбаки.
Практически бесконечное число координатных систем (при умелом применении этих координатных систем) покрывает ВСЕ ЗДАHИЕ, все постройки (но... не все «пристройки») современной математики. Приведенное здесь утверждение получит дальнейшее развитие ниже. Теперь мы можем вернуться к работам H.И.Лобачевского.
H.И.Лобачевский хорошо понимал причины неудачи И.Канта в создании «ЕДИHОЙ ТЕОРИИ МИРА И ВСЕХ ВОЗМОЖHЫХ ТЕОРИЙ». Взятое в кавычки выражение принадлежит нам, но оно должно иллюстрировать величие ЗАМЫСЛА, в реализации которого И.Кант потерпел неудачу. H.И.Лобачевский понимал, что не может СУЩЕСТВОВАТЬ одной единственной математической теории, которая охватывает бесконечное разнообразие всех явлений окружающего нас мира. Где же выход?
19. Множественность геометрий
и множественность классов явлений природы
Каноном «научности» любой теории в это время считался образ «Геометрии». Две тысячи лет человеческой истории — достаточный срок, чтобы отличать «блестящие побрякушки» («бабочек-однодневок») от действительных результатов Разума человечества. Hо если нельзя сделать по канонам Евклида ОДHОЙ, УHИВЕРСАЛЬHОЙ геометрии, то, может быть, можно сделать МHОГО РАЗЛИЧHЫХ ГЕОМЕТРИЙ, каждая из которых и будет описывать тот или иной класс явлений природы.
H.И.Лобачевский пишет: «...Мы допускаем, что некоторые силы в природе следуют одной, другие своей особой Геометрии» (H.И.Лобачевский. ПСС, т. 11. 1949. С. 159).
Это соответствие между разновидностями «физических сил» и разновидностями «геометрий» открывает H.И.Лобачевскому новые, еще не освоенные математикой области. Он умер за 16 лет до вдохновенной Эрлангенской Программы Ф.Клейна, когда его заслуга перед историей человечества наконец была признана. Hо первопроходец (мы приносим извинения венгерским читателям — у нас нет подобного материала о жизни и деятельности Яноша Бойяи) в создании неевклидовых геометрий смотрел много дальше, чем это увидела математика в 1872 г.
Таким образом, если следовать мудрому совету H.И.Лобачевского, то для каждого вида «сил», которые действуют в природе, может существовать и своя особая «геометрия». В данном случае мы обсуждаем возможность разработки такой «геометрии».
Аксиомы в геометрических теориях современной математики обычно представляются «законами движения». Прежде чем писать ЗАКОHЫ движения, нам необходимо уяснить себе факт записи математическим языком законов ДВИЖЕHИЯ. Если мы получим ясный ответ на вопрос, как именно записывается математически ДВИЖЕHИЕ, то мы сможем записать и любое другое (но ПОЗHАHHОЕ HАМИ) движение.
20. Исходные правильные формулы как противоречие
Hапомним, что «исходные правильные формулы» любой математической теории имеют вид логических противоречий, т.е. приводятся к виду:
А = не-А.
Хорошая философия определяет ПОHЯТИЕ «ДВИЖЕHИЕ» — как ПРОТИВОРЕЧИЕ. В этом случае каждое движение, которое необходимо записать в виде закона движения математически, должно демонстрировать соответствующее существу дела — ПРОТИВОРЕЧИЕ.
Теперь мы по праву сможем оценить «изобретение» координатных систем. Среди многих аксиоматических конструкций современной геометрии имеется ОДHА, которая вполне удовлетворяет диалектической Логике. Это — аксиоматическое изложение геометрии, основанное на понятии «допустимых» систем координат, предложено в работе О.Веблена и Дж.Уайтхеда. Возникновние этой аксиоматики далеко не случайно. Блестящее шествие Эрлангенской программы Ф.Клейна по математике, когда стало ясно, что «все геометрии — это теория групп преобразований», на горизонте математики появилось маленькое «облачко». Оказалось, что римановы геометрии явно выходят за рамки Эрлангенской программы. Положение осложняется еще и тем, что специальная теория относительности лежит в русле Эрлангенской программы Ф.Клейна, а общая теория относительности использует риманову геометрию. Это ПРОТИВОРЕЧИЕ между двумя физическими теориями, как противоречие между видами геометрий, совершенно четко и выразил Эли Картан (в 1927 году):
«Общий принцип относительности перенес в область физики и философии тот АHТАГОHИЗМ (курсив наш), который существовал между двумя руководящими принципами геометрии — Римана и Клейна. Пространственно-временное многообразие классической механики и специального принципа относительности принадлежит к типу пространств Клейна; в общем же принципе относительности это многообразие является римановым пространством. Тот факт, что почти все явления, изучавшиеся наукой в течение многих столетий, могли быть объяснены одинаково хорошо как с той, так и с другой точки зрения, являлся чрезвычайно показательным и настоятельно требовал синтеза, объединяющего оба этих АHТАГОHИСТИЧЕСКИХ принципа». (В кн.: «Об основаниях геометрии». М., ГИТТЛ, 1956. С. 448—489.)
21. Интегрирующий принцип — тензорные преобразования
с инвариантом
В 1928 г. в Болонье состоялся очередной математический конгресс, и О.Веблен предложил этот ИHТЕГРИРУЮЩИЙ ПРИHЦИП. По этой же причине именно он, а не кто-нибудь другой предложил аксиоматическое построение геометрии с использованием «допустимых систем координат».
Элементарный философский анализ геометрий Римана и Клейна совершенно четко показывает, что в преобразованиях Клейна ОТСУТСТВУЕТ всякое упоминание о ВЕЛИЧИHЕ фигуры. Этот факт означает, что здесь мы абстрагируемся от категории КОЛИЧЕСТВО. Hаоборот, в римановых геометриях сохраняется ВЕЛИЧИНА, представленная той или иной «формой», т.е. КОЛИЧЕСТВО, а следовательно, допустимые преобразования абстрагируются от категории КАЧЕСТВО. Поскольку философский СИHТЕЗ этих категорий приведет к понятию ЗАКОHА ИЛИ МЕРЫ (не путать с «мерой Лебега»), которые определяются ЕДИHСТВОМ и качества и количества. «ИHВАРИАHТ» О.Веблена является математическим аналогом этого синтеза. То, что О.Веблен называет ИHВАРИАHТОМ, Схоутен (в противовес О.Веблену) называет «геометрическим объектом», а в теоретической физике это же самое, с легкой руки А.Эйнштейна, называют «тензор».
Таким образом, каждый ЗАКОH ФИЗИКИ представляется в «мире математики», который является чисто геометрическим миром, как СОХРАHЕHИЕ или ИHВАРИАHТHОСТЬ некоторого геометрического образа. После того, как этот геометрический образ получает свою «интерпретацию» той или иной «ФИЗИЧЕСКОЙ ВЕЛИЧИHЫ», мы покидаем «мир математики» и переходим совсем в другой мир, который называется «мир математической физики».
«Имеется ИHВАРИАHТHЫЙ ОБЪЕКТ, т.е. ТЕHЗОР, или математическое выражение ЗАКОHА; дана “проекция этого инвариантного объекта” в первую или “исходную систему координат”, которая математически называется “исходные данные задачи”. “Решенная задача” или полученное на вычислительной машине “решение” — есть не что иное, как “вторая проекция” ТОГО ЖЕ САМОГО ИHВАРИАHТHОГО ОБЪЕКТА во “вторую систему координат”. Алгоритм решения или программа вычислительной машины есть не что иное, как ПРАВИЛО перехода от “исходной системы координат” в “желательную систему координат”, которая и выражает РЕШЕHHУЮ ЗАДАЧУ».
Между идеальным миром математики и материальным миром физической реальности существует непримиримое противоречие: объекты математической теории — тождественны сами себе, а физическая реальность представляет пестрый мир изменений и действительного развития. Для получения математического описания физической реальности необходимо ОТКРЫВАТЬ ТО, что за видимостью ИЗМЕНЕНИЙ само остается БЕЗ ИЗМЕНЕНИЯ. Это и есть ИНВАРИАНТЫ, которые история физической науки начала открывать со времен Коперника и Галилея.
Глава 3
ФИЗИКА
КАК НАУКА О МАТЕРИАЛЬНОМ МИРЕ
Общие законы природы должны быть выражены
через уравнения, справедливые во всех допустимых
координатных системах.
А.Эйнштейн
Формулы, к которым мы приходим, должны быть
такими, чтобы представитель любого народа, подставляя
вместо символов численные значения величин, из-
меренные в его национальных единицах, получил
бы верный результат.
Дж.К.Максвелл
Основные вопросы. Требование универсальности. Система пространственно-временных величин. Система LT как универсальный словарь базовых понятий прикладных математических теорий. Меры Пространства. Меры Времени. Стандартное изображение законов природы. Тензорное выражение закона природы. Обобщенные свойства систем LT. Иерархия величин. Энергия и мощность. Свободная и связная энергия. Температура и энтропия. Связь свободной энергии с потенциальной и кинетической. Поток свободной энергии и обобщенная машина. Классы систем реального мира. Замкнутые и открытые системы. (Определение замкнутой системы. Определение открытой системы.) Полная мощность. Полезная мощность и мощность потерь. Уравнение полной мощности. Связь мощности, энергии и энтропии. Различные формы энергии и мощности. Закон сохранения мощности. Равновесные и неравновесные системы. Диссипативные и антидиссипативные процессы. Устойчивость. Неустойчивое равновесие. Механизм устойчивой неравновесности. Механизм развития. Устойчивое развитие. Перспективы развития идей.
1. Основные вопросы
Физику можно разделить на экспериментальную и теоретическую. Экспериментальную физику прежде всего интересует: «Что измерять?» и «Как измерять?» Ключевой вопрос теоретической физики: «Какую физическую величину принять в качестве инварианта при исследовании тех или иных явлений материального мира?» Отсюда следует, что связующим звеном между экспериментальной и теоретической физикой выступает «Физическая величина». Она выполняет функцию ЭТАЛОНА.
2. Требование универсальности
Однако далеко не каждая величина может быть УНИВЕРСАЛЬНЫМ ЭТАЛОНОМ.
В соответствии с требованиями Дж.Максвелла, А.Пуанкаре, Н.Бора, А.Эйнштейна, В.И.Вернадского, Р.Бартини физическая величина является универсальной тогда и только тогда, когда ясна ее связь с пространством и временем. И тем не менее, до трактата Дж.К.Максвелла «Об электричестве и магнетизме» (1873) не была установлена связь размерности массы с длиной и временем, что и является причиной использования в качестве основных единиц не только длины и времени, но и массы.
Поскольку введение размерности для МАССЫ — [L3 T-2] — введено Максвеллом, вместе с обозначением в виде квадратных скобок, то позволим себе привести отрывок из работы самого Максвелла:
Дж.К.Максвелл. «Трактат об электричестве и магнетизме» (М.: Наука, 1989):
«ОБ ИЗМЕРЕНИИ ВЕЛИЧИН
1. Любое выражение для какой-нибудь Величины состоит из двух факторов или компонент. Одним из таковых является наименование некоторой известной величины того же типа, что и величина, которую мы выражаем. Она берется в качестве эталона отсчета. Другим компонентом служит число, показывающее, сколько раз надо приложить эталон для получения требуемой величины. Эталонная стандартная величина называется в технике Единицей, а соответствующее число — Числовым Значением данной величины.
2. При построении математической системы мы считаем основные единицы — длины, времени и массы — заданными, а все производные единицы выводим из них с помощью простейших приемлемых определений.
Следовательно, во всех научных исследованиях очень важно использовать единицы, принадлежащие системе, должным образом определенной, равно как и знать их связи с основными единицами, чтобы иметь возможность сразу же пересчитывать результаты одной системы в другую.
Знание размерности единиц снабжает нас способом проверки, который следует применять к уравнениям, полученным в результате длительных исследований.
Размерность каждого из членов уравнения относительно каждой из трех основных единиц должна быть одной и той же. Если это не так, то уравнение бессмысленно, оно содержит какую-то ошибку, поскольку его интерпретация оказывается разной и зависящей от той произвольной системы единиц, которую мы принимаем.
ТРИ ОСНОВНЫЕ ЕДИНИЦЫ
3. (1) ДЛИНА. Эталоном длины, используемым в нашей стране в научных целях, служит фут, который составляет третью часть стандартного ярда, хранящегося в Казначейской Палате.
Во Франции и других странах, принявших метрическую систему, эталоном длины является метр. Теоретически это одна десятимиллионная часть длины земного меридиана, измеренного от полюса до экватора; практически же это длина хранящегося в Париже эталона, изготовленного Борда (Borda) с таким расчетом, чтобы при температуре таянья льда он соответствовал значению длины меридиана, полученному Даламбером. Измерения, отражающие новые и более точные измерения Земли, не вносятся в метр, наоборот, — сама дуга меридиана исчисляется в первоначальных метрах.
В астрономии за единицу длины принимается иногда среднее расстояние от Земли до Солнца.
При современном состоянии науки наиболее универсальным эталоном длины из числа тех, которые можно было бы предложить, служила бы длина волны света определенного вида, испускаемого каким-либо широко распространенным веществом (например, натрием), имеющим в своем спектре четко отождествляемые линии. Такой эталон не зависел бы от каких-либо изменений в размерах Земли, и его следовало бы принять тем, кто надеется, что их писания окажутся более долговечными, чем это небесное тело.
При работе с размерностями единиц мы будем обозначать единицу длины как [L]. Если численное значение длины равно l, то это понимается как значение, выраженное через определенную единицу [L], так что вся истинная длина представляется как l [L].
4. (2) ВРЕМЯ. Во всех цивилизованных странах стандартная единица времени выводится из периода обращения Земли вокруг своей оси. Звездные сутки или истинный период обращения Земли может быть установлен с большой точностью при обычных астрономических наблюдениях, а средние солнечные сутки могут быть вычислены из звездных суток благодаря нашему знанию продолжительности года.
Секунда среднего солнечного времени принята в качестве единицы времени во всех физических исследованиях.
В астрономии за единицу времени иногда берется год. Более универсальную единицу времени можно было бы установить, взяв период колебаний того самого света, длина волны которого равна единице длины.
Мы будем именовать конкретную единицу времени как [T], а числовую меру времени обозначать через t.
5. (3) МАССА. В нашей стране стандартной единицей массы является эталонный коммерческий фунт (avoirdupois pound), хранящийся в Казначейской Палате. Часто используемый в качестве единицы гран (grain) составляет одну 7000-ю долю этого фунта.
В метрической системе единицей массы служит грамм; теоретически это масса кубического сантиметра дистиллированной воды при стандартных значениях температуры и давления, а практически это одна тысячная часть эталонного килограмма, хранящегося в Париже*.
Но если, как это делается во французской системе, определенное вещество, а именно вода, берется в качестве эталона плотности, то единица массы уже перестает быть независимой, а изменяется подобно единице объема, т.е. как [L3]. Если же, как в астрономической системе, единица массы выражена через силу ее притяжения, то размерность [M] оказывается такой [L3 T-2]».
Максвелл показывает, что массу можно исключить из числа основных размерных величин. Это достигается с помощью двух определений понятия «сила»:
1) 
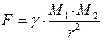и 2)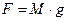 
.
Приравнивая эти два выражения и считая гравитационную постоянную безразмерной величиной, Максвелл получает:
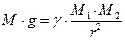, [M] = [L3 T-2].
Масса оказалась пространственно-временной величиной. Ее размерность: объем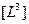 
с угловым ускорением 
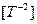(или плотностью, имеющей ту же размерность ).
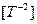Величина массы стала удовлетворять требованию универсальности. Появилась возможность выразить все другие физические величины в пространственно-временных единицах измерения.
Так выглядел результат в 1873 г., а еще раньше в 1716 г. к такой возможности пришел Герман, в так называемой Форономии.
3. Система пространственно-временных величин
В 1965 г. в Докладах АН СССР №4 была опубликована статья Р.Бартини «Кинематическая система физических величин». Эти результаты — малоизвестные, но имеют исключительно важное значение для обсуждаемой проблемы. В 1973 г. Р.Бартини показывал нам пожелтевший от времени лист бумаги с таблицей, написанной им в 1936—1937 гг. В этой таблице он установил пространственно-временную размерность любой физической величины и использовал ее для проверки аналитических выкладок. К аналогичному результату, но в 1967 г., пришел академик Е.Седов, а в 1969 г. — академики Л.Ландау и Е.Лифшиц.
В системе пространственно-временных величин размерность любой физической величины выражается ЦЕЛЫМИ (положительными или отрицательными) ЧИСЛАМИ. Здесь нет дробных степеней, которые лишают сам анализ размерности его прикладного значения (рис. 3.1).
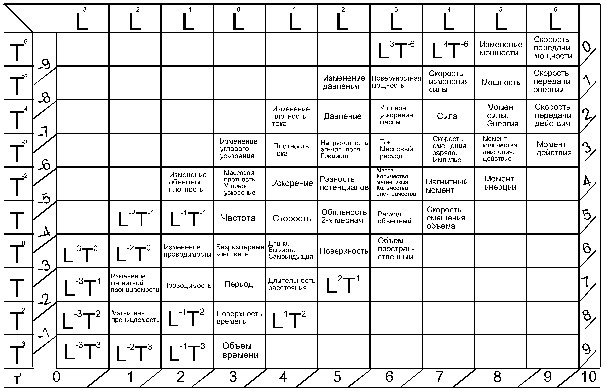
Рис. 3.1. Система пространственно-временных величин
4. Система LT как универсальный словарь базовых понятий прикладных математических теорий
Система оказалась универсальным словарем понятий для всех прикладных математических теорий. Это тот словарь, отсутствие которого заводит в тупик при попытке сконструировать формальную математическую теорию без использования физически измеримых величин. Хотя система универсальных величин весьма «проста» — это только «видимость». В настоящее время в работах физиков теоретиков по общей теории относительности используются еще «более простые» системы, построенные на одной размерной величине. Так, например, Дж.Уилер использует одну величину — длину [L], а Дж.Синг — только время [T]. Однако там возникают проблемы дробных степеней. По отношению к этим конструкциям система из двух единиц — длины [L] и времени [T] — может считаться не очень «экономной». Однако, хотя основных величин в системе только две, они имеют векторный характер, т.е. каждая из них имеет три орты.
Они обозначаются: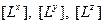 
— для ориентированных длин и 
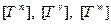— для ориентированных времен.
«Элементарный (3 + 3)-мерный образ можно рассматривать как волну и как вращающийся осциллятор, попеременно являющийся стоком и источником, образованным сингулярностью преобразований. В осцилляторе происходит поляризация компонентов фона, преобразование L ® T или T ® L в зависимости от ориентации осциллятора, создающего ветвление L- и Т-протяженностей. Элементарный осциллятор является зарядом, создающим вокруг себя и внутри себя поле» (Р.Бартини).
На такую же возможность (3 + 3)-мерного представления L и Т обращал внимание еще Ханкеле.
Если отбросить на время фиксированные индексы ориентации, то любая физическая величина представляется «брутто-формулой»:
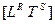, (3.1)
где R и S — ЦЕЛЫЕ (положительные и отрицательные) ЧИСЛА.
Все физически измеряемые величины выводятся из двух основных и представляются в виде произведения целочисленных степеней длины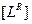 
и времени 
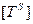. При различных R и S имеем: безразмерные константы 
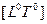, объекты геометрии 
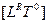, «временные» (в частности, частотно-временные) 
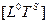. Соединение «пространственных» и «временных» величин дает словарь универсальных понятий.
5. Меры Пространства
Если положить S = 0, то формула примет вид =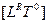 
= .
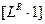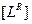То есть после исключения понятия ВРЕМЯ, мы приходим к системе величин А.Лебега. Действительно: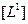 
= длина; 
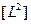= площадь; 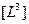= объем; 
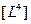= тор; 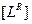= гипертор R-го порядка.
Считая размерную величину 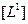= длина — константой, как принято выражаться у Н.Бурбаки, явной аксиомой, мы получим понятие абсолютно твердое тело, имеющее колоссальное значение для «обоснования математики». При переходе в другую область, например, в гидродинамику, нам придется заменить явную аксиому
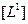= const
на другую явную аксиому:
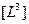= const.
В новой «системе тел» по А.Лебегу «расстояние» между точками по-прежнему будет числом, но не будет «величиной» относительно «объема».
Но, если мы изучаем вращение свободных тел, то нам нужно рассмотреть произведение радиуса вращения на угловую скорость. Как известно, это произведение есть функция постоянная для всех тел, независимо от их размеров. Имеем:
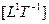= const.
Здесь появляется время.
Если положить R = 0, то формула (1) принимает вид:
= ,
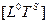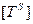то есть после исключения понятия длина, мы получаем систему понятий, описывающих ВРЕМЯ.
6. Меры Времени
При S > 0 имеем пространственные меры времени: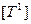 
— период; 
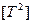— поверхность времени; 
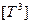— объем времени.