«Являются ли координаты A( , ) координатами ТОЙ ЖЕ САМОЙ ТОЧКИ, которая имеет координаты B( , ) во второй системе координат?»
Вот здесь возможен ОДИН И ТОЛЬКО ОДИН ОТВЕТ: либо «ДА», либо «НЕТ».
Никакой другой способ не дает «математически чистого» определения булевой переменной. Теперь мы можем получить и ПОНЯТИЕ «АЛГОРИТМ».
Это ПРАВИЛО-F, которое позволяет по координатам ОДНОЙ И ТОЙ ЖЕ ТОЧКИ, данным в первой системе координат, найти координаты той же самой точки во второй системе координат.
B( 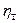 ,
,  ) = F & A(
) = F & A( 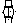 ,
, 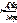 ).
).
Фактически существуют три правила, которые позволяют математику говорить «СЛЕДОВАТЕЛЬНО»:
1. 1. Если А > B и B > C, то, следовательно, A > C.
2. 2. Если A = B и B = C, то, следовательно, A = C.
3. 3. Если A Î B и B Î C, то, следовательно, A Î C.
Устройство математики, благодаря ее аксиоматической конструкции, позволяет передавать ВСЕ, ЧТО ПОНЯТО в вычислительную машину. Это открывает возможность создания «банка теорий», охватывающих все предметные области, т.е. все профессиональные знания.
Подведем итог: аксиомы, которые правильно называть ПРЕДПОЛОЖЕНИЯМИ, не могут рассматриваться без своего «отрицания», т.е. ПРОТИВОПОЛОЖЕНИЯ. Всякое ПОЛОЖЕНИЕ во всех случаях имеет ГРАНИЦУ, за пределами которой оно «превращается» в свою ПРОТИВОПОЛОЖНОСТЬ. Этот переход за ненаблюдаемую в математике ГРАНИЦУ, есть изменение КАЧЕСТВА. Этот переход через ГРАНИЦУ, т.е. переход к другому КАЧЕСТВУ, порождает известные математические «трудности»: нелинейность, бифуркацию, катастрофу и т.п. — математические термины, выражающие РАЗРЫВ непрерывности, СКАЧЕК или изменение ПРАВИЛА.
Именно И.Кант обнаружил, что невозможно описывать реальный мир, если пользоваться ТОЛЬКО УТВЕРДИТЕЛЬНЫМИ ВЫСКАЗЫВАНИЯМИ. Оказалось, что мы нуждаемся в ОТРИЦАТЕЛЬНЫХ высказываниях. Отдельные части реальности удовлетворяют утвердительным положениям, но существуют и такие части реальности, которые требуют ОТРИЦАНИЯ этих утвердительных положений. Анализ этой ситуации и привел к признанию сосуществования как утверждения, так и его отрицания. Объединение того и другого философы называют СИНТЕЗИСОМ, который охватывает как ТЕЗИС, так и АНТИТЕЗИС. Новое КАЧЕСТВО — есть НОВЫЙ ОБЪЕКТ. Именно он и есть ИНВАРИАНТ математического описания, а «старые» тезис и антитезис — есть не более как его «координатные представления».
4. О единстве и целостности математики
Требование ЕДИНСТВА или ЦЕЛОСТНОСТИ математической теории неясно витало и витает в сознании выдающихся людей различных эпох. Уже в своеобразном «манифесте» группы Н.Бурбаки мы встречаем крушение замысла унификации всей математики у пифагорейцев — «все вещи суть числа», но открытие иррациональности — отвергло эту попытку унификации. Хотя и принято считать, что унификации математики посвящено многотомное издание Н.Бурбаки, мы хотели бы выделить Эрлангенскую программу Ф.Клейна в качестве первой современной попытки унификации ВСЕЙ МАТЕМАТИКИ (1872 г.).
5. Математика и геометрия
Догадка, которой руководствовался Ф.Клейн, состояла в том, что ВСЯ математика может быть представлена как разновидности ПРОЕКТИВНОЙ ГЕОМЕТРИИ. Он писал:
«Между приобретениями, сделанными в области геометрии за последние пятьдесят лет, развитие проективной геометрии занимает первое место. Если в начале казалось, что для нее недоступно изучение так называемых метрических свойств, так как они не остаются без изменения при проектировании, то в новейшее время научились представлять и их с проективной точки зрения, так что теперь проективный метод охватывает всю геометрию». (Об основаниях геометрии. М., ГИТТЛ, 1956. С. 399.) Ф.Клейн считал, что ему удалось специфицировать типы геометрий с помощью ГРУПП ПРЕОБРАЗОВАНИЙ КООРДИНАТ.
Не очень бросается в глаза, что метрика, доступная проективной геометрии — это метрика, которая позволяет разделить на две равные части отрезок или увеличить отрезок в два раза. Таким образом эта метрическая шкала состоит из чисел, которые кратны 2n или 2 - n. Само собою разумеется, что это дискретная шкала, которая (в прикладных теориях, использующих вычислительные машины) вполне достаточна для всех технических приложений.
Другой подход к единству ВСЕЙ ГЕОМЕТРИИ был продемонстрирован Д.Гильбертом в его работах по основаниям геометрии. Гильберт положил в основу различия геометрий — различие в использовании АКСИОМ. Рассматривая каждую аксиому и ее отрицание, Гильберт предъявил не только не-евклидовы геометрии, но и не-дезарговы, не-архимедовы, не-паскалевы и др. геометрии. У Гильберта было введено 16 аксиом. Если считать, что все приведенные им аксиомы НЕЗАВИСИМЫ, то мы должны обозревать и «узнавать в лицо» — 216 геометрий, каждая из которых может быть выделена последовательностью из нулей и единиц (в зависимости от принятия данной аксиомы — 1, а если данная аксиома отрицается, то 0) — 65 536 различных геометрий. При интерпретации каждой в той или иной предметной области — мы можем получить такое количество качественно различных физических теорий.
Третий подход к единству ВСЕЙ ГЕОМЕТРИИ идет от О.Веблена. Не задерживаясь на антагонизме геометрий Клейна и Римана, блестяще разобранных Э.Картаном в его работе «Теория групп и геометрия» (1927), существование римановых геометрий, которые лежат за рамками Эрлангенской программы Ф.Клейна, привело О.Веблена и Дж.Уайтхеда к работе «Основания дифференциальной геометрии». Там О.Веблен упоминает о своем докладе на международном математическом конгрессе в Болонье. О.Веблен ожидал синтеза всех геометрий, как «...теорию пространств с инвариантом». Здесь мы встречаемся с понятием «РАЗМЕРНОСТЬ», которое будет иметь весьма важное значение в нашем последующем изложении. Развитием этого направления служит четырехтомное издание работ японской ассоциации прикладной геометрии (RAAG), изданных в 1955—1968 гг. на основе работ Г.Крона.
Хотя японская ассоциация и объявила работы Г.Крона «Новой эпохой в науке», только в Японии мы находим развитие идей Г.Крона. К сожалению в России и Европе идеи Г.Крона малоизвестны.
Многие ли математики в то время были знакомы с возможными обобщениями N-мерных пространств, о которых пишет Г.Крон (1939 г.):
«...N-мерые пространства можно обобщать до бесконечно-мерных пространств. Кроме того, вместо использования только четырех-, пяти- и вообще целочисленно-размерных пространств можно использовать 2/3-, 4,375- или p-мерные пространства, включающие все типы сложных структур. Эти пространства используются в исследовании более фундаментальных электродинамических явлений».
Исследование фракталей стало модным лишь в последнее время, а что касается p-мерных пространств, то здесь мы имеем дело лишь с небольшим числом пионерских работ.
Само собою разумеется, что наличие экспериментальных данных с одной стороны, и невозможность их теоретического обоснования — с другой стороны, ставит нас перед естественным вопросом: как должна быть изменена ТЕОРИЯ, чтобы:
1) она СОХРАНЯЛА действующую ТЕОРИЮ там, где ее выводы соответствуют (и нашли экспериментальное подтверждение) наблюдаемым фактам;
2) она ИЗМЕНЯЛА действующую ТЕОРИЮ там, где ее выводы не соответствуют некоторой группе экспериментальных данных (лежащих за ГРАНИЦЕЙ существующей ТЕОРИИ).
Не подлежит никакому сомнению, что подобное РАСШИРЕНИЕ действующей теории должно включать в себя (но уже на правах ЧАСТНОГО СЛУЧАЯ) уже СУЩЕСТВУЮЩУЮ теорию (теории).
Ответ лежит не в области физики, а в области математики. Мы должны РАЗЛИЧАТЬ те положения, которые принадлежат миру МАТЕМАТИКИ, от тех положений, которые связаны с ФИЗИЧЕСКОЙ ИНТЕРПРЕТАЦИЕЙ математической теории.
6. Устройство математических теорий
Изучение этой проблемы показало, что существуют и такие «теоретики», которые имеют слабое представление об устройстве математических теорий, полностью перенося выводы аксиоматики математических оснований на реальный мир. Для математической теории нет и не может быть ГРАНИЦ применимости: в математической теории ВСЕГДА получаемые выводы находятся в соответствии с принятыми ПРЕД-посылками. Это соответствие СЛЕДСТВИЙ принятым ПРЕД-посылкам называется ИСТИННОСТЬЮ математической теории. В этом смысле математик может заменять некоторые предпосылки на то, что раньше называлось следствием, но при этом сама математическая теория не теряет своей истинности. Такую переработку некоторых математических теорий совершила группа, публиковавшая свои материалы под псевдонимом Н.Бурбаки. Многотомное издание современной математики группой Н.Бурбаки имело своим основанием своеобразный «стандарт» или «технические условия», которым должна удовлетворять любая МАТЕМАТИЧЕСКАЯ теория. Этот же «стандарт» применяется и при переходе от одной теории к другой.
Заметим, что «стандарт», определенный для устройства математических теорий, данный Бурбаки, является НЕОБХОДИМЫМ для передачи формальной теории в вычислительную машину.
Рассмотрим «стандарт», который предложен группой Н.Бурбаки.
Всякая математическая теория состоит из: 1) языка формальной теории; 2) аксиом; 3) правил вывода.
Наличие указанных трех составных частей характеризует ЛЮБУЮ МАТЕМАТИЧЕСКУЮ ТЕОРИЮ. Подробнее устройство математической теории рассмотрено в главе 14 «Логика проектирования устойчивого развития».
7. Отличие математического языка от естественного
Введенный группой Н.Бурбаки язык — язык теории множеств — являясь унифицированным языком математики, имеет кардинальное отличие от естественного языка. В математической теории не только следствия находятся в однозначном соответствии с принятыми предпосылками, но имеется такое же взаимнооднозначное соответствие между ТЕРМОМ (или термином) и обозначаемым этим термом математическим ОБЪЕКТОМ.
Математический объект всегда выведен из под действия ВРЕМЕНИ. Это выражается в том, что некоторые формулы принято называть в математике АТОМАМИ (или АТОМАРНЫМИ ВЫСКАЗЫВАНИЯМИ). Атом несет в себе два значения: неделимый и объект, который не изменяется с ходом действительного времени. Последнее должно означать, что обозначенный этим термом или соотношением объект так же не изменяется, как не изменяется (по написанию) его «имя».
Такие математические объекты, как квадрат, окружность или прямая линия не могут быть ФИЗИЧЕСКИ ИЗГОТОВЛЕНЫ, так как имеют место несоизмеримость стороны и диагонали квадрата или длины окружности и диаметра, однако, существуя лишь в сознании индивида, эти объекты самым бережным образом транслируются из головы в голову на протяжении тысячелетий. Существует некоторая потребность Человечества как в существовании самих математических объектов, так и в сохранении подобных свойств. Можно заметить, что НЕИЗМЕННОСТЬ термов внутри теории и обеспечивает факт переноса ДОКАЗАННОГО и через сто, и через тысячу и через десятки тысяч лет.
Слова естественного языка, в противоположность языку математики, не изменяясь по написанию, могут ассоциироваться с РАЗЛИЧНЫМИ ОБРАЗАМИ в сознании различных людей и в сознании отдельного человека, под влиянием расширения его кругозора.
8. Интерпретация математических теорий
Интерпретация математической теории ВСЕГДА имеет границы применимости, ибо однозначное соответствие получаемых СЛЕДСТВИЙ принятым АКСИОМАМ (другое название ПРЕД-посылок) соответствует ЛИНЕЙНОМУ МИРУ, а физическая реальность поражает нас своей существенной НЕЛИНЕЙНОСТЬЮ. Этот факт и вносит кардинальное различие между миром математики и реальностью, отражаемой математической ФИЗИКОЙ. Мы нуждаемся в таком МАТЕМАТИЧЕСКОМ определении НЕЛИНЕЙНОСТИ, которое, будучи перенесенным в прикладную область, позволяло ИЗМЕНЯТЬ АКСИОМЫ (ПРЕД-посылки), сохраняя старую теорию в тех границах, где она соответствует наблюдаемым фактам. Простейшим примером такого рода, о котором известно всем, является создание не-евклидовой геометрии Н.И.Лобачевским и Я.Бойяи. Такое изменение АКСИОМ сохраняет старую теорию и, в то же время, позволяет существовать НОВОЙ теории.
Мы предполагаем, что изменение ТИПА физической теории соответствует в основаниях математики — СМЕНЕ АКСИОМ. Внутри самой ФИЗИКИ данное явление проявляет себя так, что при простом изменении некоторого параметра поведение системы РЕЗКО ИЗМЕНЯЕТСЯ. Предсказания старой теории в этой области перестают соответствовать экспериментальным данным, наблюдаемым в этой области. Такое изменение поведения системы при изменении некоторого параметра можно называть «бифуркацией», можно описывать подобные изменения особой теорией («теория катастроф»), но существо дела этим не объясняется.
Перейдем к третьему вопросу.
9. Почему ЗНАНИЕ математики не гарантирует УМЕHИЯ ей пользоваться
в конкретном проектировании систем?
Тот, кто когда-нибудь пережил «ОЗАРЕНИЕ» легко поймет, что всякое математическое описание той или иной предметной области, это — ВСПЫШКА, которая так правильно названа «ОЗАРЕНИЕМ». Озарение «не-логично», вернее, оно «не-логично» в смысле математической логики. Если всякий акт творчества, как «не-логичный», можно считать ЧУДОМ, то все творческие люди, хотя они и не волшебники, но они... «учатся» волшебству.
Если принять во внимание, что каждое такое ЧУДО являет себя в математической форме, то НЕОБХОДИМОСТЬ владения математикой не подлежит сомнению. Тем не менее, как и принято в математике, необходимое условие еще не является условием ДОСТАТОЧНЫМ. Именно эта «недостаточность» чисто математического образования и не позволяет РЕГУЛЯРНО творить ЧУДЕСА, что легко обнаруживается при переходе от «высказываний» на естественном языке к логическим формам математики.
Известно, что в грамматическом предложении мы выделяем подлежащее и сказуемое. Подлежащим обычно является имя существительное, а роль сказуемого выполняет глагол.
Хотя процесс превращения «подлежащего» грамматической формы в «субъект» логической формы и «сказуемого» грамматической формы в «предикат» логической формы потребовал тысячелетий развития культуры научного мышления, мы должны зафиксировать терминологическое различие грамматической формы от логической формы. Это означает, что термин «подлежащее» как и термин «сказуемое» мы будем использовать для описания грамматической формы предложения, а термины «субъект» и «предикат» только для описания логической формы суждения.
Уже грамматическая форма предложения намечает расчленение явлений наблюдаемого мира на два больших класса:
— класс предметов (пространственно-протяженных тел);
— класс движений (характеризуемых длительностью).
Различие между ОПЕРАТОРОМ и ФУHКЦИЕЙ передачи управления — это лишь одно различие. Хотелось провести еще одно расчленение: расчленение ОБЪЕКТА, над которым осуществляется ОПЕРАЦИЯ, и самого ОПЕРАТОРА, который осуществляет эту операцию.
Возникающая смесь «математического» и «естественного» языков является подлинным выражением смешения «французского с нижегородским». Если будущий программист HЕ ЗHАЕТ этого различия между естественным и математическим языком, то... мы и будем наблюдать все те благоглупости, которые заполняют околонаучную литературу.
10. Классификатор возможных задач
Учитывая специфические особенности вычислительных машин и специфику самой математики, мы можем дать следующий классификатор ВСЕХ (!) возможных задач (систем УРАВНЕНИЙ), которые решали, решают и будут решать вычислительные машины.
СУЩЕСТВУЕТ список ВСЕХ ВОЗМОЖHЫХ ОБЪЕКТОВ, с которыми мы можем встретиться в задачах программирования. Они различаются друг от друга «РАЗМЕРHОСТЬЮ". Размерность является «ИМЕHЕМ КАЧЕСТВА» математического объекта. Hабор «ИМЕH» мы берем из языка ГЕОМЕТРИИ. Фактически это «размерность симплекса» комбинаторной топологии. Итак:
1. 1. Hульмерный симплекс — «точка».
2. 2. Одномерный симплекс — «отрезок» или 1-длина.
3. 3. Двумерный симплекс — «площадка» или 2-длина.
4. 4. Трехмерный симплекс — «объем» или 3-длина.
5. 5. Четырехмерный симплекс — ... или 4-длина.
. . .
K. K-мерный симплекс — ... или K-длина.
Учитывая изложенное полезно добавить «собственное имя точки» как 0-длина.
11. Введение системы координат
Превращение геометрического объекта соответствующей размерности в математический ТЕКСТ предполагает введение той или иной системы координат. Очевидно, что «размерность» координатной системы (для размещения геометрического объекта!) должна быть как минимум HА ЕДИHИЦУ РАЗМЕРHОСТИ БОЛЬШЕ.
Так, например, для помещения «точки» нам необходима координатная система типа «отрезок» или 1-длина. В вычислительной машине может располагаться лишь конечное число точек, т.е. точки на отрезке «занумерованы» в виде булевых переменных. Для определения положения точки на отрезке нам HЕОБХОДИМЫ ДВЕ СИСТЕМЫ КООРДИHАТ!
Что это означает? Две системы координат позволяют ЗАДАВАТЬ ВОПРОС примерно такого типа: «Является ли число А координатой ТОЙ ЖЕ САМОЙ ТОЧКИ, которая обозначена числом В в другой системе координат?» Если ответ положителен, то мы говорим «ДА». Если ответ отрицателен, то мы говорим «HЕТ». Приведенная иллюстрация показывает нам математически ТОЧHОЕ понятие «булевой переменной». Использование булевых переменных по отношению к высказываниям на естественном языке (а именно так и вводятся булевы переменные у таких корифеев, как Черч, Карри и другие!) — является и философским и математическим невежеством.
Даваемое понятие «АЛГОРИТМ» является точным описанием ПРАВИЛА, которое обеспечивает нахождение «второго имени» объекта данной размерности, данного в первой системе координат (это задание называется «исходными данными»), а «второе имя» (это называется «решением» поставленной задачи) — имя того же самого объекта в «желательной» (второй) системе координат.
Точно так же, как мы дали «имена» самим геометрическим объектам, можно дать «имена» всем возможным системам координат.
Такой перенумерованный список всех возможных систем координат и дает нам правило для записи алгоритмов.
12. Правило записи алгоритма
Алгоритм определяется ТРЕМЯ «ИМЕHАМИ»:
1. 1. Именем геометрического объекта.








