«Властивості відображення,що співставляє кожному метричному компакту сімейство його непустих компактних підмножин»
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМ. І. СІКОРСЬКОГО”
Фізико-математичний факультет
Кафедра диференціальних рівнянь
Курсова робота
з дисципліни «Диференціальні рівняння»
«Властивості відображення,що співставляє кожному метричному компакту сімейство його непустих компактних підмножин»
Виконав: студент гр. ОМ-61
Мартинов Д.О.
Затвердив: Пелюх Г. П.
Київ 2018
Зміст
Вступ ................................................................................................................................................ 1
1.Основні визначення і попередні результати. ............................................................................... 1
2.Основні результати ...................................................................................................................... 2
3.Приклади ...................................................................................................................................... 3
4.Додаткові властивості відображення Н ......................................................................................... 5
Список літератури............................................................................................................................ 5
Вступ
В даній праці досліджуються властивості відображення H, що співставляє кожному метричному компакту сімейство його непустих компактних підмножин. Показано, що це відображення є неперервним и 1-ліпщецевим. Існує гіпотеза, що не буває бієкція ізометрій простору Громова-Хаусдорфа на собі, окрім тотожного відображення Н, можливо, є ізометричним вкладенням простору Громова-Хаусдорфа в себе. В праці приведено декілька класів прикладів просторів, відстань між якими зберігається при даному відображенні. В доповненні наводяться властивості, які можливо спрощуют доведення ізометричності Н.
1.Основні визначення і попередні результати.
Нехай А- довільна множина. Через #А будемо позначати потужність множини А. Нехай Z - довільний метричний простір. Відстань між його точками x i y будемо позначати через |xy|. Через diam Z позначимо діаметр Z. Якщо X,Y C Z – непорожні підмножини, то покладемо |XY|=inf{|xy|:x 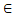 X, y
X, y 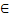 Y}, а |XY|’=sup{|xy|:x
Y}, а |XY|’=sup{|xy|:x 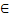 X, y
X, y 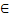 Y}. Якщо X={x}, то замість |{x}Y|=|Y{x}| i |{x}Y|=|Y{x}|’ будемо писати |xY|=|Yx| i |xY|’=|Yx|’ відповідно.
Y}. Якщо X={x}, то замість |{x}Y|=|Y{x}| i |{x}Y|=|Y{x}|’ будемо писати |xY|=|Yx| i |xY|’=|Yx|’ відповідно.
Для непорожніх X,Y C Z положимо 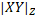 =max{
=max{ 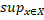 |xY|,
|xY|, 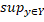 |yX|}. Отримана величина називається відстанню Хаусдорфа між X i Y. Сім’єю усіх непорожніх замкнутих обмежених підмножин метричного простору Z позначимо через H(Z). Відомо[1],що H(Z) з відстанню Хаусдорфа є метричним простором.
|yX|}. Отримана величина називається відстанню Хаусдорфа між X i Y. Сім’єю усіх непорожніх замкнутих обмежених підмножин метричного простору Z позначимо через H(Z). Відомо[1],що H(Z) з відстанню Хаусдорфа є метричним простором.
Нехай X i Y – метричні простори. Трійка (X’,Y’,Z), яка складається з метричного простору Z і двух його підмножин X’ i Y’, ізометричних відповідно X i Y, називається реалізацією пари (X,Y). Відстанню 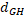 (X,Y) по Громову-Хаусдорфу між X i Y називається точна нижня грань чисел r, для яких існує реалізація (X’,Y’,Z) пари (X,Y) така, що
(X,Y) по Громову-Хаусдорфу між X i Y називається точна нижня грань чисел r, для яких існує реалізація (X’,Y’,Z) пари (X,Y) така, що 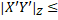 r. На множині М всіх компактних метричних просторів, які розглядаються с точністю до ізометрії, функція
r. На множині М всіх компактних метричних просторів, які розглядаються с точністю до ізометрії, функція 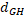 (X,Y) є метрикою[1].
(X,Y) є метрикою[1].
Метричний простір називається симплексом, якщо всі його ненульові відстані однакові. Зауважимо, що симплекс компактний, тоді і тільки тоді, якщо він скінчений. Симплекс, який складається з n точок , відстань між якими дорівнює t , позначимо через t 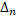 . Якщо t=1, то простір t
. Якщо t=1, то простір t 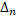 будемо для стислості позначати
будемо для стислості позначати 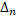 .
.
Озачення 1.1.(|2|). Для натуральних p , q і речових t , s > 0, має місце:
2 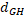 (t
(t 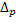 , s
, s 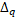 )=
)= 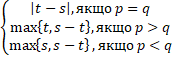
Озачення 1.2.(|2|). Нехай М-кінцевий метричний простір, n =# M . Тоді для кожного m 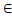 N , m > n , t > 0, маємо:
N , m > n , t > 0, маємо:
2 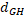 (t
(t 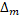 , M)=max{t,diam M – t}.
, M)=max{t,diam M – t}.
Для довільного метричного простору М положимо :
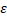 (М)=inf{|xy|:x,y
(М)=inf{|xy|:x,y 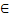 M, x
M, x 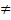 y}.
y}.
Озачення 1.3.(|2|). Нехай М- кінцевий метричний простір і n =# M , тоді
2 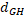 (t
(t 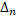 , M)=max{t-
, M)=max{t- 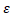 (М),diam M – t}.
(М),diam M – t}.
Нехай М – довільна множина, тоді через 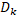 (M) позначимо сім’ю всеможливих розбиттів М на k його непорожніх підмножин. Нехай тепер М – метричний простір і D={
(M) позначимо сім’ю всеможливих розбиттів М на k його непорожніх підмножин. Нехай тепер М – метричний простір і D={ 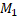 ,
, 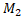 ,…,
,…, 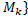
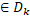 (M). Положимо diam D = max(diam
(M). Положимо diam D = max(diam 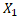 , …, diam
, …, diam 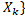 ,
, 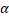 (D)=
(D)= 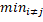 |
| 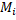 ,
, 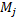 |, а
|, а 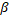 (D)=
(D)= 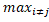 |
| 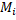 ,
, 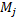 |’.
|’.
Озачення 1.4.(|2|). Нехай М- компактний метричний підпростір і m 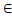 N , m<#M. Тоді для будь-якого t >0, виконується
N , m<#M. Тоді для будь-якого t >0, виконується
2 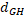 (t
(t 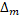 , M)=inf{max{diam D, t -
, M)=inf{max{diam D, t - 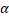 (D),
(D), 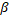 (D) – t): D
(D) – t): D 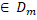 (M)}.
(M)}.
2.Основні результати
Відомо[1], що якщо Х-компактний метричний простір, то H(X)- також компакт. Розглянемо відображення H:M 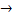 M,що співставляє кожному метричному компакту X сім‘ю всіх його непорожніх компактних підмножин. Доведемо, що відображення Н є 1-липщецевим.(и,слідовно,неперервним).
M,що співставляє кожному метричному компакту X сім‘ю всіх його непорожніх компактних підмножин. Доведемо, що відображення Н є 1-липщецевим.(и,слідовно,неперервним).
Нехай 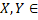 M-неізометричні метричні компакти, і
M-неізометричні метричні компакти, і 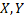 ізометрично вкладені в метричний простір Z. В силу компактності Y, для будь-якого x
ізометрично вкладені в метричний простір Z. В силу компактності Y, для будь-якого x 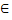 X існує y’
X існує y’ 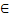 Y таке, що |xY|=|xy’|. Введемо позначення y’=
Y таке, що |xY|=|xy’|. Введемо позначення y’=  (x), тим самим визначив відображення
(x), тим самим визначив відображення  : X
: X 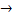 Y. Нехай А С X – довільна замкнута підмножина, тоді
Y. Нехай А С X – довільна замкнута підмножина, тоді 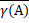
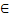 H(Y), де
H(Y), де 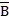 означає замкнення підмножини В метричного простору. Доведемо декілька теорем, що описують властивості компакта
означає замкнення підмножини В метричного простору. Доведемо декілька теорем, що описують властивості компакта 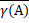 .
.
Озачення 2.1. Для будь-якого A 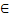 H ( X ) i a
H ( X ) i a 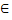 A маємо | a
A маємо | a 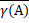 |=| a
|=| a 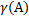 |
|
Д-ня.В силу визначення  , для будь-якого y
, для будь-якого y 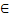 Y справедливо, що |ay|
Y справедливо, що |ay| 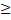 |a
|a  (a)|, тому |a
(a)|, тому |a 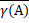 |=
|= 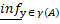 |ay|=|a
|ay|=|a 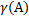 |, так як
|, так як 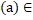
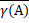 .
. 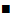
Озачення 2.2. Для будь-якого A 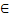 H ( X ) , виконується
H ( X ) , виконується 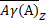 =
= 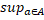 | a
| a  ( a )|.
( a )|.
Д-ня. Нехай 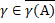 . Роздивимося два випадки.
. Роздивимося два випадки.
1.Якщо 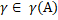 , то існує
, то існує 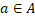 таке, що y=
таке, що y= 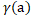 . Але так як |yA|=
. Але так як |yA|= 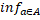 |ya|, то |yA|
|ya|, то |yA| 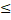 |a
|a  (a)|.
(a)|.
2.Якщо 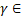
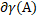 ,то існує послідовність
,то існує послідовність 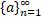 точок из А така,що
точок из А така,що  (
( 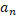 )
) 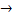 y при n
y при n 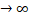 . Так як в метричному компакті будь-яка послідовність точко має східну послідовність, то, без обмеження спільності, можно вважати ,що
. Так як в метричному компакті будь-яка послідовність точко має східну послідовність, то, без обмеження спільності, можно вважати ,що 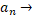 a
a 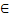 A. Припустимо,що |a
A. Припустимо,що |a  (a)| < |ay|, тоді
(a)| < |ay|, тоді 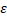 :=|ay|-|a
:=|ay|-|a  (a)|>0. Існує номер k>0 такий, що |a
(a)|>0. Існує номер k>0 такий, що |a 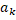 | <
| <  i |y
i |y  (
( 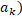 |<
|< 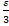 . Із нерівності трикутника для ay
. Із нерівності трикутника для ay 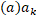 отримуєм:
отримуєм:
| 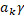 (a)|
(a)| 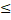 |a
|a  (a)|+|a
(a)|+|a 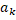 |<|a
|<|a  (a)|+
(a)|+ 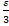 =|ay|-
=|ay|- 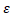 +
+  =|ay| -
=|ay| - 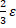 <|ay|-| a
<|ay|-| a 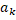 |-|y
|-|y  (
( 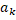 )|
)| 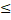 |
| 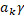 (
( 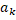 )|, протиріччя з визначенням
)|, протиріччя з визначенням  (
( 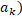 . Отже |ay|=|a
. Отже |ay|=|a  (a)| i, слідовно, |yA|
(a)| i, слідовно, |yA| 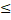 | a
| a  (a)|.
(a)|.
Отже, для будь-якого 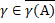 існує
існує 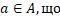 |yA|
|yA| 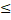 | a
| a  (a)|, звідки
(a)|, звідки 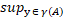 |yA|
|yA| 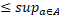 |a
|a  (a)|. Отже, в силу теореми 2.1,
(a)|. Отже, в силу теореми 2.1, 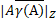 =max{
=max{ 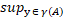 |yA|,
|yA|, 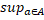 |a
|a  (a)|}=
(a)|}= 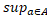 |a
|a  (a)|, що і потрібно було довести.
(a)|, що і потрібно було довести.  .
.
Наслідок 2.1. Для будь-якого A 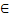 H ( X ) має місце
H ( X ) має місце 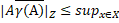 | x
| x  ( X )|.
( X )|.
Озачення 2.3. Для будь-яких A 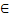 H ( X ) і В
H ( X ) і В 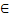 H ( Y ) маємо
H ( Y ) маємо 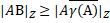 .
.
Д-ня. Зауважимо, що для будь-якого а 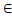 А має місце |aB|=
А має місце |aB|= 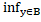 |ay|
|ay| 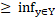 |ay|
|ay| 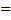 |a
|a 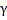 (a)|. Отже,
(a)|. Отже, 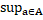 |aB|
|aB| 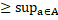 |a
|a 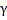 (a)|=
(a)|= 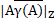 , тому
, тому 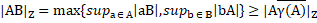 , що і потрібно було довести.
, що і потрібно було довести. 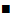
Наслідок 2.2. Для будь-якого A 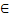 H ( X ) має місце: | AH ( Y )|=
H ( X ) має місце: | AH ( Y )|= 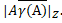
Теорема 2.1. Нехай X i Y – метричні компакти, занурені в метричний простір Z , тоді 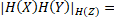
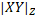 .
.
Д-ня. Зауважимо, що із наслідку 2.1 випливає обмеженість усіх відстаней 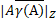 величиною
величиною 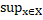 |x
|x 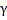 (X)|, а , значить,
(X)|, а , значить, 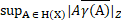
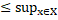 |x
|x 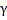 (X)|=
(X)|= 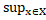 |xY|. Беручи до уваги наслідок 2.2, маємо що
|xY|. Беручи до уваги наслідок 2.2, маємо що 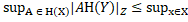 |xY|. З іншою сторони, для будь якого x
|xY|. З іншою сторони, для будь якого x 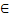 X виконується |x
X виконується |x  (x)|=
(x)|= 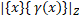 =
= 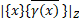 . Отже,
. Отже, 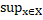 |xY|=
|xY|= 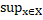 |x
|x 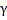 (X)|
(X)| 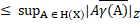 =
= 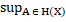 |
| 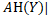 . Таким чином,
. Таким чином, 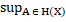 |
| 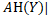 =
= 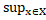 |xY|. Побудувавши аналогічне
|xY|. Побудувавши аналогічне  відображення
відображення 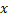 :Y
:Y 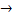 X, отримаємо, що
X, отримаємо, що 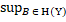 |
| 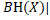 =
= 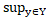 |yX|. Але тоді
|yX|. Але тоді 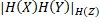 =
= 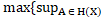 |
| 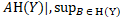 |
| 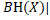 }=
}= 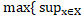 |xY|,
|xY|, 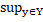 |yX|}=
|yX|}= 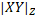 , що и треба було довести.
, що и треба було довести. 
Теорема 2.2. Для будь-яких метричних компактів X i Y виконується : 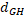 ( H ( X ), H ( Y ))
( H ( X ), H ( Y )) 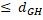 ( X , Y ).
( X , Y ).
Д-ня. Із теореми 2.1 випливає, що якщо для X,Y існує реалізація (X,Y,Z) така, що 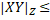 g, то для H(X), H(Y) існує реалізація (H(X), H(Y), H(Z)) така, що
g, то для H(X), H(Y) існує реалізація (H(X), H(Y), H(Z)) така, що 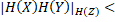 g. Тоді, в силу визначення відстані по Громову-Хаусдорфу,
g. Тоді, в силу визначення відстані по Громову-Хаусдорфу, 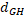 (H(X), H(Y))
(H(X), H(Y)) 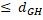 (X,Y).
(X,Y).
Наслідок 2.3. Відображення Н неперервне.
Наслідок 2.4. Відображення Н є 1-ліпщецевим.
Д-ня. Із теореми 2.2 випливає, що відображення Н є ліпшецевим с константою С, де С 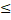 1. Покажемо, що С=1.Відомо, що відстань від одноточкового простору до будь-якого метричного простору дорівнює половині діаметра. Очевидно, що H({x})={x} і d(H(Y))=d(Y), де d(X)- діаметр простору Х. Отже, |{x}Y|=|H({x})H(Y)|. Тому С
1. Покажемо, що С=1.Відомо, що відстань від одноточкового простору до будь-якого метричного простору дорівнює половині діаметра. Очевидно, що H({x})={x} і d(H(Y))=d(Y), де d(X)- діаметр простору Х. Отже, |{x}Y|=|H({x})H(Y)|. Тому С 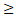 1, отже С=1.
1, отже С=1. 
3.Приклади
В цьому розділі будуть побудовані декілька класів прикладів, в яких зберігається відстань Громова-Хаусдорфа між X i Y, при відображенні Н.
Означення 3.1. Відображення Н зберігає відстань між симплексами.
Д-ня. Відмітимо, що H(t 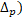 =t
=t 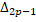 . Отже, згідно з формулою, що вказана в означенні 1.1, Н зберігає відстань Громова-Хаусдорфа між довільними кінцевими симплексами.
. Отже, згідно з формулою, що вказана в означенні 1.1, Н зберігає відстань Громова-Хаусдорфа між довільними кінцевими симплексами. 
Означення 3.2. Нехай М-кінцевий простір m =# M , n 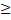 m i t > 0, тоді
m i t > 0, тоді 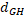 ( t
( t 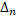 , M )
, M ) 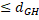 ( H ( t
( H ( t 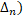 , H ( M )).
, H ( M )).
Д-ня. Відмітимо, що 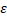 (М)=inf{|xy|:x,y
(М)=inf{|xy|:x,y 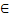 M, x
M, x 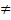 y}=
y}= 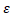 (H(М)) i diam X = diam H(X). Із означення 1.2 і означення 1.3 випливає те, що нам потрібно.
(H(М)) i diam X = diam H(X). Із означення 1.2 і означення 1.3 випливає те, що нам потрібно. 
Покажемо наступну оцінку відстані Хаусдорфа.
Означення 3.3. Нехай X ={ 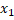 ,
, 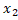 ,…
,… 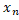 } i Y ={
} i Y ={ 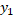 ,
, 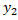 ,…
,… 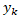 } – кінцеві метричні підпростори Z , тоді для будь-якої перестановки
} – кінцеві метричні підпростори Z , тоді для будь-якої перестановки 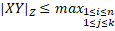 |
| 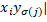
Д-ня. Відмітимо, що для будь-якої точки 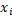 маємо |
маємо | 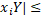 |
| 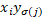 |, отже
|, отже 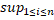 |
| 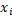 Y|
Y| 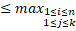 |
| 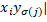 . Аналогічно,
. Аналогічно, 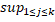 |
| 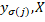 |
| 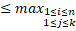 |
| 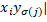 , значить і
, значить і 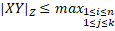 |
| 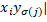 , що і потрібно було довести.
, що і потрібно було довести. 
Для побудови ще одного класа прикладів потрібно довести наступний факт (ідея доведення взята з [3]).
Означення 3.4. Якщо X - зв ’ язний метричний компакт, то H ( X ) теж зв ‘ язне.
Д-ня. Відмітимо, що якщо X зв’язний, то зв’язна і будь-яка його степінь ( 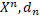 ), де
), де 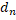 (x,x’)=
(x,x’)= 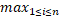 d(
d( 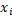 ,
, 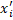 ). Роздивимося вкладення
). Роздивимося вкладення 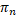 :
: 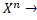 H(X), певне наступним чинном:
H(X), певне наступним чинном: 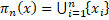 . Очевидно, що
. Очевидно, що 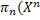 ) є сім’єю усіх кінцевих підмножин X з не більш, чим n елементами. В силу означення 3.3 ,
) є сім’єю усіх кінцевих підмножин X з не більш, чим n елементами. В силу означення 3.3 , 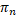 є 1-ліпшицевим, а отже, неперервним. Отже
є 1-ліпшицевим, а отже, неперервним. Отже 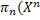 ) буде зв’язним, тому що
) буде зв’язним, тому що 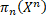
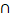
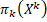 =
= 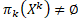 , при всіх k
, при всіх k 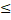 n. Але кінцеві множини скрізь щільні в H(X),отже, H(X)=
n. Але кінцеві множини скрізь щільні в H(X),отже, H(X)= 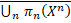 також зв’язане, як замикання зв’язаного простору.
також зв’язане, як замикання зв’язаного простору. 
Доведемо наступну властивість зв’язаних просторів
Означення 3.5. Якщо X = 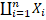 - з в’язаний метричний простір, то для будь-якого натурального i
- з в’язаний метричний простір, то для будь-якого натурального i 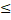 n існує j
n існує j 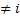 таке, що |
таке, що | 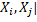 =0
=0
Д-ня. Покажемо, що якщо для деякого натурального I при будь-яких j 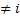 виконується |
виконується | 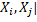 >0, то Х не зв’язний.
>0, то Х не зв’язний.
Доведемо спочатку це твердження для випадку n=2. Припустимо, що X= 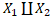 , де |
, де | 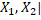 >0. Покажемо, що |
>0. Покажемо, що | 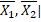 =inf{|x₁,x₂|:x₁
=inf{|x₁,x₂|:x₁ 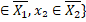 >0, де
>0, де 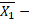 замкнення. Підмітимо, що для будь-яких x₁
замкнення. Підмітимо, що для будь-яких x₁ 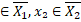 існують послідовності
існують послідовності 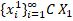 i
i 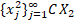 , для яких
, для яких 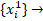 x₁ , i
x₁ , i 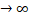 , a
, a 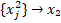 , j
, j 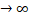 . Але тоді |x₁
. Але тоді |x₁ 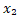 |
| 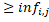 |
| 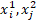 |, отже, |x₁
|, отже, |x₁ 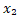 |>0, тобто |
|>0, тобто | 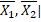 > 0. Але
> 0. Але 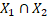 =
= 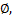 а отже і
а отже і 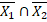 =
= 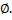 Виходить, що ми представили Х як об’єднання двох непорожніх замкнутих перетинаючихся підмножин
Виходить, що ми представили Х як об’єднання двох непорожніх замкнутих перетинаючихся підмножин 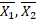 , а отже і Х – не зв’язний.
, а отже і Х – не зв’язний.
А зараз нехай n>2. Роздивимося будь-яке 1 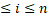 . Припустимо, що для будь-якого j
. Припустимо, що для будь-якого j 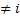 , маємо |
, маємо | 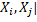 >0. Але тоді |
>0. Але тоді | 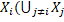 )|>0, так як у нас скінченне число множин. Використовуючи випадок n=2, отримаємо, що Х знову не зв’язний.
)|>0, так як у нас скінченне число множин. Використовуючи випадок n=2, отримаємо, що Х знову не зв’язний. 
Означення 3.6. Нехай Х – зв’ язний метричний компакт, тоді для будь-якого дійсного числа t такого, що t 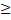 diam X , ш будь-якого натурального р маємо:
diam X , ш будь-якого натурального р маємо:
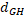 ( t
( t 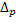 , X )
, X ) 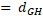 ( H ( t
( H ( t 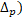 , H ( X )).
, H ( X )).
Д-ня. Покажемо, що 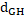 (t
(t 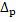 ,X)=
,X)=  t =
t = 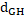 (H(t
(H(t 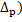 ,H(X)). Для цього використаємо формулу із означення 1.4: 2
,H(X)). Для цього використаємо формулу із означення 1.4: 2 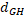 (t
(t 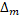 , M)=inf{max{diam D, t -
, M)=inf{max{diam D, t - 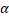 (D),
(D), 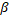 (D) – t): D
(D) – t): D 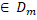 (M)}. Відмітимо, що для будь –якого розбиття D виконується diam D
(M)}. Відмітимо, що для будь –якого розбиття D виконується diam D 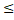 diam X
diam X 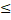 t і
t і 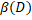 =
= 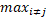 |
| 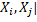 ’
’ 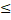 diam X
diam X 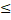 t. В силу означення 3.5, маємо
t. В силу означення 3.5, маємо 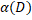 =
= 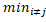 |
| 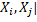 =0, тому t -
=0, тому t - 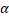 (D)=t. Отже, max{diam D, t -
(D)=t. Отже, max{diam D, t - 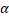 (D),
(D), 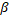 (D) – t)=t, а отже,
(D) – t)=t, а отже, 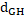 (t
(t 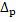 ,X)=
,X)=  t.
t.
В силу того, що Н зберігає зв’язність (означення 3.4) і діаметр, для Н(Х) вірні ті ж міркування, тому 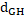 (H(t
(H(t 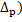 ,H(X))=
,H(X))= 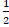 t, що і потрібно було довести.
t, що і потрібно було довести. 
4.Додаткові властивості відображення Н
В цьому розділі наводяться міркування, які можуть допомогти в доведенні ( або в знаходженні контр-прикладу) ізометричності Н.
Означення 4.1. Припустимо, що відображення Н зберігає відстань між точками деякої скрізь щільної підмножини 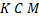 . Тоді Н ізометрична на всій М.
. Тоді Н ізометрична на всій М.
Д-ня. Так як Н є 1-ліпщецевим( наслідок 2.4), то воно, очевидно, зберігає збіжність. Тепер нехай X i Y – деякі метричні компакти, тоді, в силу скрізь щільності K в M, існують послідовності метричних просторів 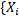 } i {
} i { 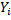 } із К такі, що
} із К такі, що 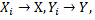 при i
при i 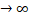 . Тоді H(
. Тоді H( 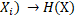 , а H(
, а H( 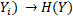 , більше того, в силу нерівності трикутника,
, більше того, в силу нерівності трикутника, 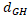 (
( 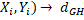 (
( 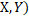 , а
, а 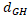 (
( 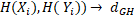 (
( 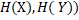 при i
при i 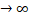 . Якщо Н зберігає відстань між компактами із К, то для будь-якого натурального і має місце
. Якщо Н зберігає відстань між компактами із К, то для будь-якого натурального і має місце 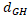 (
( 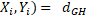 (
( 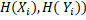 , отже
, отже 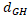 (
( 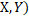 =
= 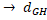 (
( 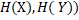 для будь-яких метричних компактів X і Y, що і було потрібно.
для будь-яких метричних компактів X і Y, що і було потрібно. 
Наслідок 4.1. Якщо обмеження Н на множині усіх кінцевих метричних просторів ізометричне, то воно ізометричне на всій М
Кінцевий метричний простір назвемо простором загального положення, якщо всі його відстані попарно різні, а нерівність трикутника завжди строге.
Наслідок 4.2. Якщо Н зберігає відстань між просторами загального положення з однаковим числом точок, то воно ізометричне на всій М.
Список літератури 








