3 Пучок кривых второго порядка
Пусть M1, M2, M3, M4, — четыре точки, не лежащие на одной прямой. Задавая по произволу еще одну точку M5 (не коллинеарную никаким трем из точек M1, M2, M3, M4, получим, по теореме 1, единственную кривую второго порядка, проходящую через точки M1, M2, M3, M4, и точку M5 .
Поэтому множество всех кривых второго порядка, проходящих через четыре точки M1, M2, M3, M4, бесконечно. Это множество кривых называется пучком кривых второго порядка, определяемым точками M1, M2, M3, M4.
Будем обозначать кривую той же буквой F, которой обозначена левая часть F(x, у) ее уравнения (1), так что F и λ F при любом λ ≠0 — это одна и та же кривая. Если
F (х, y) = λ 1 F 1 (x, y) + λ 2 F 2 (x, y),
то будем говорить, что кривая F есть линейная комбинация (с коэффициентами λ 1 и λ 2) кривых F1 и F2. Если кривые F1 и F2 принадлежат пучку, определяемому точками M i = (x i , y i ) (i = l, 2, 3, 4), то уравнения F1(x, у)=0 и F2(x, у)=0 удовлетворяются, если в них подставить значения х = xi , у = yi при любых i = l, 2, 3, 4. Но тогда и уравнение λ 1 F 1 (x, y) + λ 2 F 2 (x, y)=0 будет при х = xi , у = yi удовлетворяться. Другими словами, всякая кривая, являющаяся линейной комбинацией двух (или более) кривых, принадлежащих данному пучку, принадлежит этому пучку. Докажем обратное предложение. Пусть в пучке кривых второго порядка выбраны две определенные кривые F1 и F2. Тогда всякая кривая F данного пучка есть линейная комбинация этих двух кривых F1 и F2.
Пусть пучок определен четверкой точек M1, M2, M3, M4. Возьмем на кривой F какую-нибудь точку M5, не коллинеарную ни с какими тремя из точек M1, M2, M3, M4. Кривая F есть единственная кривая второго порядка, проходящая через точки M1, M2, M3, M4, M5. Поэтому для доказательства сделанного утверждения достаточно найти такую линейную комбинацию λ 1 F 1 + λ 2 F 2 чтобы кривая
λ 1 F 1 (x, y) + λ 2 F 2 (x, y)=0 (12)
проходила через точку M5 = (х5, у5), т. е. достаточно определить λ 1 и λ 2, вернее, их отношение λ 1: λ 2, из условия
λ 1 F 1 (х5, у5) + λ 2 F 2 (х5, у5), (13)
Итак, любой пучок кривых второго порядка вполне определен, если даны две какие-нибудь кривые F 1 и F 2 из этого пучка: он состоит из всех кривых, являющихся линейными комбинациями λ 1 F 1 + λ 2 F 2 двух данных. Все эти кривые определяются значениями одного параметра— отношением λ = λ1: λ 2 двух коэффициентов в линейной комбинации λ 1 F 1 + λ 2 F 2. Другими словами, пучок кривых второго порядка является одномерным многообразием кривых — совершенно в том же смысле, в каком пучок прямых является одномерным многообразием прямых (а пучок плоскостей —
 |
одномерным многообразием плоскостей).
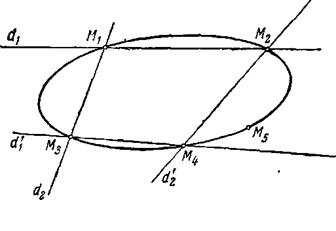
Понятие пучка кривых позволяет очень просто найти уравнение кривой второго порядка, проходящей через заданные пять точек M1, M2, M3, M4, M5. В самом деле, возьмем четыре точки из числа данных пяти, например M1, M2, M3, M4.
Легко написать уравнения прямых:
d 1 : M 1 M 2 d ′1: M 3 M 4 ,
d 2 : M 1 M 3 d ′2: M 2 M 4 .
Теперь имеем две распадающиеся кривые второго порядка: кривую F1 распадающуюся на пару прямых d 1 и d ′1, и кривую F2, распадающуюся на прямые d 2 и d ′2 . Многочлены F1(х, у) и F2(х, у) суть произведения трехчленов первой степени, являющихся левыми частями уравнений, соответствующих прямым d 1 и d ′1, d 2 и d ′2. Распадающиеся линии F1 и F2, очевидно, проходят через точки M1, M2, M3, M4 т. е. принадлежат пучку, определяемому этими точками. Остается только определить отношение λ1: λ 2 из условия, чтобы кривая λ 1 F 1 + λ 2 F 2 проходила через точку M5 = (х5, у5), этим условием является равенство (13), из которого находим
λ1: λ 2 = - F 2 (х5, y 5 ) : F 1 ( x 5 , у5).








