Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
9 класс Алгебра 06.03.2023
Тема: Формулы n-го члена арифметической и геометрической прогрессий, суммы первых n членов.
Цели: вывести формулу суммы первых п членов арифметической прогрессии; формировать умение применять эту формулу при решении задач.
Ход урока
I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
II. АКТУАЛИЗАЦИИ ЗНАНИЙ.
Являются ли арифметическими прогрессиями последовательности чисел:
3, 7, 12, … (нет) 28, 31,34… (да)
Дайте определение арифметической прогрессии.
an +1 = an + d .
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Как называется каждый компонент этой формулы?
Как найти разность арифметической прогрессии? (d = an +1 - an )
Любая арифметическая прогрессия может быть задана формулой вида an = kn + b , где k и b – некоторые числа
Какие из формул задают арифметическую прогрессию: an = 5 n + 7 , a n =3n2+1, a n =4 – n 3 , an = 3 – 4 n?
Найти 5-ый член числовой последовательности заданной формулой an = 5 n + 7 (32)
Найти 4-ый член числовой последовательности заданной формулой an = 3 – 4 n (-13)
Чему равна разность арифметической прогрессии: 3; 0; -3; -6; … (-3)
Продолжите арифметическую прогрессию: 28, 31,34… Ответ: 37,40,43…
Найдите пятый член арифметической прогрессии: 3; 7; 11; … (19)
III. ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА И ЗАКРЕПЛЕНИЕ ЗНАНИЙ В СТАНДАРТНОЙ СИТУАЦИИ.
Скажите, сколько времени вам понадобится для того, чтобы сложить, к примеру, все натуральные числа от 1 до 100?
S = 1 + 2 + 3+ …+98 + 99 + 100,
S = 100 + 99 + 98+ …+3 +2 +1,
2 S = 101∙100, S = 
=5050.
Сумму п первых членов арифметической прогрессии принято обозначать как Sn. Вывод формулы проведем в ходе решения задачи «Найти сумму п первых членов арифметической прогрессии, если известны ее первый и n-ый члены.»
Запишите в тетради.
(аn) – арифметическая прогрессия.
Sn = a1 + a2 + a3 + … + an-2 + an-1 + an,
Sn = an + an-1 +an-2 + …+ a3+ a2 + a1.
a2 + an-1 = (a1 + d) + (an – d) = a1 + an,
a3 + an-2 = (a1 + 2d) + (an– 2d) = a1 + an,
a4 + an-3 = (a1 + 3d) + (an– 3d) = a1 + an и т.д.
2Sn = (a1 + an)∙n.
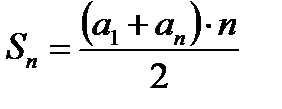
Используя формулу решите № 603(а) стр.158
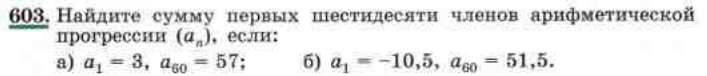
S60 =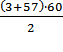 
= 60 ∙ 30 = 1800.
Решите № 605(а) стр.158.
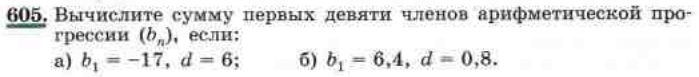
Удобно ли применить формулу, применительно к данной задаче? Что из условия известно? Ваши предложения по решению?
Выведем в общем виде вторую формулу суммы n-первых членов арифметической прогрессии, если известны a1 и d. Запишите формулы в тетради.
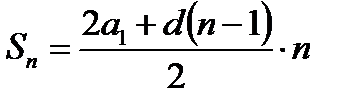
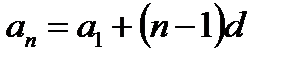Если учесть, что , то получим:
№605(а) Решение.
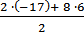S9 =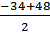 
∙9 = 
∙ 9 =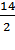 
∙ 9 = 7 ∙ 9 = 63.
IV. ЗАКРЕПЛЕНИЯ ЗНАНИЙ. № 607(а), 609(а, в)
V. ДОМАШНЕЕ ЗАДАНИЕ.
П. 26 стр. 154-158 выучить формулы, выполнить №604, 606 (а,в)