Возведение в степень
Эти две операции — возведение в степень и взятие логарифма — одинаково
просты или сложны для понимания, ведь между ними много общего . На самом
деле они противоположны друг другу: одна операция отменяет другую . Если
выбрать какое-то число, возвести его в степень, а затем взять логарифм от ре-
зультата, то мы получим то самое число, с которого начали . Как бы то ни было,
со степенями мы в повседневной жизни сталкиваемся намного чаще, поэтому
они нас не так ужасают . Начнем с них . 
502
Приложение . Математика
Операция возведения в степень означает, что мы берем некое число, на-
зываемое основанием, и возводим его в степень другого числа . То есть попросту
умножаем основание само на себя ровно столько раз, в какую степень его
требуется возвести . Основание записывается в виде обычного числа, а сте-
пень — в виде индекса сверху . Вот несколько простых примеров:
22 = 2 ∙ 2 = 4,
25 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32,
43 = 4 ∙ 4 ∙ 4 = 64 .
(Мы используем точку для обозначения операции умножения, а не символ ×,
так как его очень легко перепутать с буквой x.) Один из самых удобных случа-
ев возведения в степень — тот, когда в качестве основания берется число 10;
в этом случае степень соответствует просто-напросто числу нулей справа от
единицы:
101 = 10,
102 = 100,
109 = 1 000 000 000,
1021 = 1 000 000 000 000 000 000 000
В этом и заключается идея возведения в степень . Если говорить конкретно
о показательной функции, то здесь мы имеем в виду, что фиксируем какое-то
определенное основание и позволяем степени, в которую возводится это ос-
нование, быть переменной величиной . Если обозначить основание через a,
а степень — через x, то получим:
a x = a ∙ a ∙ a ∙ a ∙ a ∙ a … a ∙ x раз .
К сожалению, это определение может создавать впечатление, что показа-
тельная функция имеет смысл только в том случае, если степень x — это по-
ложительное целое число . Как умножить число на само себя минус два раза?
Или 3,7 раза? Здесь вам остается только верить, что магия математики позво-
ляет определять показательную функцию для любого значения x . Результатом
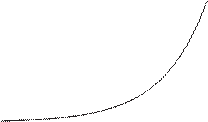
является гладкая функция с очень маленьким значением, когда x — отрицатель-
ное число, но резко возрастающая, когда x становится положительным, как
показано на рис . П1 .
Что касается показательных функций, есть две важные вещи, о которых
необходимо помнить . Любое основание, возведенное в степень 0, равно 1, 
Приложение . Математика
10
8
6
4
2
10
x
503
–1
–0,5
0
0,5
1
x
Рис . П1 . Показательная функция 10x . Обратите внимание, что она возрастает так быстро,
что совершенно невозможно изобразить ее для больших значений x
а любое основание, возведенное в степень 1, равно самому себе . Для основания
10 это выглядит так:
100 = 1,
101 = 10 .
Если степень — это отрицательное число, то результатом операции явля-
ется число, обратное результату возведения в соответствующую положительную
степень:
10–1 = 1/101 = 0,1,
10–3 = 1/103 = 0,001 .
То, что вы видите выше, — это всего лишь конкретные примеры из бо-
лее общих свойств, которым подчиняется показательная функция . Одно
из этих свойств является невероятно важным: если умножить два числа,
представляющих собой одно и то же основание, возведенное в разные степе-
ни, то при перемножении степени складываются, а основание остается тем
же самым:
10x ∙ 10y = 10(x+y) .
То же верно и в обратную сторону: показательная функция от суммы сте-
пеней равна произведению двух чисел, равных основанию, возведенному в эти
степени .1 











































504
Приложение . Математика
Большие числа
Нетрудно понять, почему показательная функция так полезна: числа, с кото-
рыми нам приходится иметь дело, иногда бывают чрезвычайно большими,
а с помощью возведения в степень вы можете превратить число средней вели-
чины в просто огромное . Как мы обсуждали в главе 13, количество различных
состояний, необходимых для описания возможных конфигураций нашего со-
путствующего объема Вселенной, равно примерно
120
Это число настолько неимоверно, невообразимо огромное, что было бы
совершенно непонятно, с какой стороны вообще подступиться к его описанию,
если бы на помощь не пришло возведение в степень .
Давайте рассмотрим несколько других больших чисел, для того чтобы
оценить, насколько огромно это . Один миллиард равен 109, тогда как один
триллион — это 1012; с этими значениями мы хорошо знакомы благодаря
обсуждениям экономики и правительственных трат . Количество частиц
в нашей наблюдаемой Вселенной составляет около 1088; настолько же велика
была энтропия в ранние времена . Теперь, когда у нас есть черные дыры, эн-
тропия наблюдаемой Вселенной равна приблизительно 10101, хотя вполне
могла бы дорасти до 10120 . (Это число, 10120, также представляет собой от-
ношение предсказываемого значения плотности энергии вакуума к наблюда-
емой плотности .)
Для сравнения, энтропия макроскопического объекта, такого как чашка
кофе, — где-то 1025 . Это значение сравнимо с числом Авогадро, которое равно
6,02 ∙ 1023 — примерно столько атомов составляют один грамм водорода . Чис-
ло песчинок на всех пляжах Земли — приблизительно 1020 . Число звезд в ти-
пичной галактике — около 1011, а число галактик в наблюдаемой Вселенной —
около 1011, то есть в наблюдаемой Вселенной существует примерно 1022
звезд — немного больше, чем песчинок на Земле .
Базовые единицы измерения, используемые физиками, — это единицы
времени, длины и массы; используются также их комбинации . Самый короткий
интервал времени, представляющий интерес, — это планковское время, при-
мерно 10–43 секунд . Предположительно инфляция продолжалась около10–30 се-
кунд или меньше, хотя это значение чрезвычайно неточно . Вселенная создала
гелий из протонов и нейтронов где-то через 100 секунд после Большого взры-
ва, а прозрачной стала в момент рекомбинации, 380 000 лет (1013 секунд)
спустя . (В одном году около 3 ∙ 107 секунды .) Сейчас наблюдаемой Вселенной 
|
Приложение . Математика
505
14 миллиардов лет (примерно 4 ∙ 1017 секунды) . Еще через 10100 лет или около
того все черные дыры практически полностью испарятся, оставив после себя
холодную и пустую Вселенную .
Самая маленькая длина — это планковская длина, около 10–33 сантиметров .
Размер протона — примерно 10–13 сантиметров, а размер человеческого суще-
ства — примерно 102 сантиметров (это очень низкое человеческое существо,
но мы сейчас оперируем приблизительными значениями) . Расстояние от Зем-
ли до Солнца — около 1013 сантиметров; расстояние до ближайшей звезды —
около 1018 сантиметров, а размер наблюдаемой Вселенной — около 1028 сан-
тиметров .
Планковская масса — это примерно 10–5 граммов; для отдельной частицы
это было бы невероятно много, но по макроскопическим стандартам — совсем
нет . Самые легкие частицы с ненулевой массой — нейтрино; мы даже пока не
знаем точно, какова их масса, но минимальная вроде бы составляет около 10–36
граммов . Масса протона — приблизительно 10–24 граммов, а человеческого
существа — примерно 105 граммов . Солнце весит около 1033 граммов, галак-
тика — около 1045 граммов, а масса, содержащаяся в пределах наблюдаемой
Вселенной, составляет около 1056 граммов .
Логарифмы
Логарифмическая функция — самая простая вещь на свете: она всего лишь
отменяет показательную функцию . Если у нас есть какое-то число, которое
может быть выражено в форме 10x, а это возможно для любого положительно-
го числа, то логарифм этого числа равен просто2
lg(10x) = x .
Что может быть проще? Точно так же возведение в степень отменяет лога-
рифм:
10lgx = x .
Можно также думать об этом так: если число представляет собой целую
степень десяти (например, 10, 100, 1 000 и т . п .), то логарифм — это просто-
напросто число нулей справа от единицы:
lg(10) = 1,
lg(100) = 2,
lg(1000) = 3 . 
506
lg(x)
2
1,5
1
0,5
Приложение . Математика
0
20
40
60
80
100
x
–0,5
–1
Рис . П2 . Логарифмическая функция lg(x) . Она не определена для отрицательных значений x,
и по мере приближения x к нулю справа значение логарифма стремится к минус бесконеч-
ности
Однако так же как и показательная функция, логарифм — это гладкая функ-
ция, как показано на рис . П2 . Логарифм числа 2,5 равен 0,3979, логарифм 25
равен примерно 1,3979, логарифм 250 — примерно 2,3979 и т . д . Единственное
ограничение заключается в том, что невозможно взять логарифм от отрица-
тельного числа, и это разумно, так как логарифм отменяет показательную
функцию, а получить отрицательное число в результате операции возведения
в степень невозможно . Грубо говоря, для больших чисел логарифм — это про-
сто «количество цифр в числе» .
Логарифм демонстрирует свойство, аналогичное тому, с которым мы уже
познакомились выше для возведения в степень (результат возведения в степень,
равную сумме чисел, равен произведению соответствующих степеней): лога-
рифм произведения равен сумме логарифмов, то есть
log(x ∙ y) = log(x) + log(y) .
Это чудесное свойство делает логарифмы невероятно полезными для изуче-
ния энтропии . Как мы обсуждали в главе 8, физическое свойство энтропии
заключается в том, что энтропия двух систем после объединения равна сумме
энтропий этих систем по отдельности . Но число возможных состояний объеди-
ненной системы равно произведению количеств возможных состояний двух
систем . Поэтому Больцман сделал вывод о том, что энтропия должна быть
равна логарифму числа состояний, а не самому числу состояний . В главе 9 мы
рассказали схожую историю, но уже для информации: Шэннон хотел найти
меру информации, для которой общая информация, переданная в двух неза- 





















































Приложение . Математика
507
висимых сообщениях, была бы равна сумме количеств информации в каждом
из сообщений, и он также прибегнул к помощи логарифма .
Проще говоря, логарифмы обладают таким милым свойством, что они берут
огромные числа и стачивают их до управляемых размеров . Беря логарифм от
такого тяжеловесного числа, как миллиард, мы получаем симпатичную девятку .
Логарифм — функция монотонная, то есть его значение всегда увеличивается
по мере увеличения значения, от которого берется логарифм . Таким образом,
логарифм предоставляет специфическую меру того, насколько число велико,
но при этом сжимает громадные числа до разумных размеров, что чрезвычай-
но полезно в таких областях, как космология, статистическая механика и даже
экономика .
В заключение необходимо отметить, что, так же как и степенная функция,
логарифмы могут браться по разным основаниям . «Логарифм по основанию b»
числа x — это степень, в которую необходимо возвести b, для того чтобы полу-
чить x:
log2(2x) = x,
log12(12x) = x
и т . д . Если мы не записываем основание явно, то подразумевается, что оно
равно 10, потому что именно таким количеством пальцев обладает большинство
людей . Однако ученые и математики частенько используют нечто странное,
а именно натуральный логарифм, который часто записывается как ln(x) и ос-
нованием в котором служит число Эйлера:
ln(x) = loge(x),
e = 2,7182818284…
Число Эйлера — это иррациональное число, как π или квадратный корень
из двух, так что в десятичной записи, которая частично показана выше, оно
продолжается бесконечно . На первый взгляд кажется, что использовать нечто
подобное в качестве основания логарифма невероятно странно . Но в действи-
тельности если углубиться в математику, то выяснится, что число e обладает
множеством приятных свойств: в математическом анализе, например, функ-
ция e x — единственная (за исключением вырожденной функции, всегда равной
нулю), которая равна своей производной, а также интегралу от себя самой .
В этой книге все наши логарифмы брались по основанию 10 и обозначались lg,
но если вы решите взяться за физику и математику на высшем уровне, то буде-
те постоянно встречаться с натуральными логарифмами . 
508
Примечания
Приложение . Математика
1
2
Эти свойства — часть той же «магии математики», о которой мы упоминали выше . На-
пример, нам интересно было бы понять, что означает «возвести 10 в степень 0,5» . Я знаю,
что какими бы ни оказались реальные числа, должно выполняться свойство 100,5 ∙ 100,5 =
10(0,5+0,5) = 101 = 10 . Другими словами, если мы умножим число 100,5 на само себя, то полу-
чим 10; это означает, что 100,5 должно быть всего лишь квадратным корнем из 10 (это
рассуждение верно и для любого другого основания, возведенного в степень 0,5) . С по-
мощью этого трюка мы можем понять, каким будет результат возведения любого основа-
ния в любую другую степень .
Здесь везде используются десятичные логарифмы, поэтому мы обозначаем их lg . Лога-
рифмы по основанию, отличному от 10, обозначаются как logax, где a — основание .
Скажем, если бы речь шла о логарифме от x по основанию 2, мы бы обозначили его
log2x . — Примеч. пер . 
Благодарности
Для того чтобы выпестовать книгу — от концепции до публикации, необходи-
мо приложить большие коллективные усилия, и я должен поблагодарить мно-
жество людей, которые помогали мне на этом пути . В период, когда существо-
вали еще только лишь неясные очертания будущей книги, мне посчастливилось
повстречать, полюбить и создать семью с женщиной, которая оказалась неве-
роятно талантливым писателем и популяризатором науки . Я бесконечно благо-
дарен Дженнифер Оллетт ( Jennifer Ouellette), благодаря которой эта книга
стала несравнимо лучше, а весь процесс обрел смысл .
Я разослал черновики рукописи многим своим друзьям, и в ответ они при-
слали мне массу шутливых комментариев и кучу до невозможности разумных
предложений по улучшению . Огромное спасибо Скотту Ааронсону (Scott
Aaronson), Эллисон Беатрис (Allyson Beatrice), Дженни Чен ( Jennie Chen),
Стивену Фладу (Stephen Flood), Дэвиду Гре (David Grae), Лорен Гандерсон
(Lauren Gunderson), Робину Хэнсону (Robin Hanson), Мэтту Джонсону (Matt
Johnson), Крису Лакнеру (Chris Lackner), Тому Левенсону (Tom Levenson),
Карен Лорре (Karen Lorre), Джорджу Массеру (George Musser), Хью Прайсу
(Huw Price), Тэду Пайну (Ted Pyne), Мари Рути (Mari Ruti), Алексу Сингеру
(Alex Singer) и Марку Троддену (Mark Trodden) за то, что не давали сбиться
с пути истинного . Подозреваю, что многие из них в скором будущем примутся
за написание собственных книг, и я буду счастлив прочитать каждую .
На протяжении многих лет я обсуждал стрелу времени и другие вопросы,
о которых говорится в этой книге, с коллегами-учеными, и теперь уже невоз-
можно сказать, кто из них в какой степени повлиял на формирование моей
точки зрения . Помимо перечисленных выше первых читателей, я хочу поблаго-
дарить Энтони Агирре (Anthony Aguirre), Дэвида Альберта (David Albert),
Андреаса Альбрехта (Andreas Albrecht), Тома Бэнкса (Tom Banks), Рафаэля
Буссо (Raphael Bousso), Эдди Фари (Eddie Farhi), Брайана Грина (Brian Greene),
Джима Хартла ( Jim Hartle), Курта Хинтербихлера (Kurt Hinterbichler), Тони
Леггетта (Tony Leggett), Андрея Линде (Andrei Linde), Лауру Мерсини (Laura
Mersini), Кена Олума (Ken Olum), Дона Пейджа (Don Page), Джона Прескил- 
510
Благодарности
ла ( John Preskill), Игги Савики (Iggy Sawicki), Козму Шализи (Cosma Shalizi),
Марка Средники (Mark Srednicki), Кипа Торна (Kip Thorne), Алекса Виленки-
на (Alex Vilenkin) и Роберта Уайлда (Robert Wald) (а также остальных, кого я,
к стыду своему, забыл упомянуть) за все разговоры, которые мы вели в течение
этих лет . Особую благодарность я хочу выразить Дженни Чен ( Jennie Chen),
которая не только внимательно прочитала рукопись, но также оказала неоце-
нимую поддержку в период, когда я лишь начинал всерьез заниматься изучени-
ем стрелы времени .
Сам я в последнее время был довольно нерадивым ученым, работая над
завершением книги в то время, пока мои коллеги в одиночку форсировали наши
совместные исследовательские проекты . Так что спасибо и простите меня,
Лотти Акерман (Lotty Ackerman), Мэтт Бакли (Matt Buckley), Клаудиа де Рам
(Claudia de Rham), Тим Дюлане (Tim Dulaney), Эдриэн Эриксек (Adrienne
Erickcek), Мойра Грешем (Moira Gresham), Мэтт Джонсон (Matt Johnson),
Марк Камионковски (Marc Kamionkowski), Сонни Мантри (Sonny Mantry),
Майкл Рэмси-Масолф (Michael Ramsey-Musolf), Лиза Рэнделл (Lisa Randall),
Хейвуд Там (Heywood Tam), Чин-Яо Цен (Chien-Yao Tseng), Инганн Вехас
(Ingunn Wehus) и Марк Вайз (Mark Wise), за то, что вам в последнее время
постоянно приходилось мириться с моей отстраненностью и невозможностью
сосредоточиться на задачах .
Катинка Мэтсон (Katinka Matson) и Джон Брокман ( John Brockman) су-
мели превратить мои первоначальные идеи в основательный замысел для новой
книги и постоянно двигали процесс вперед . Я познакомился с моим редактором
Стивеном Морроу (Stephen Morrow) задолго до того, как мысль о написании
книги вообще пришла мне в голову, и мне было чрезвычайно приятно порабо-
тать с ним . Джейсон Торчински ( Jason Torchinsky) взял мои жалкие наброски
и превратил их в привлекательные иллюстрации . Каким-то образом Майкл
Берубе (Michael Bérubé), при посредничестве Эллиота Тарабура (Elliot
Tarabour), сумел предложить свою помощь в рецензировании книги еще до
того, как она была фактически написана . Но учитывая тематику — природа
времени, — чего еще можно было ожидать?
Я принадлежу к тому типу людей, которых утомляет длительная работа дома
или в офисе, поэтому частенько я собираю свои бумаги и учебники по физике
и устраиваюсь с ними в ресторане или кофейне, для того чтобы сменить обста-
новку . Неизбежно кто-нибудь подойдет и спросит, что я читаю, и — вместо
того чтобы убежать в страхе перед всей этой грозной наукой и математикой —
начнет задавать вопросы о космологии, квантовой механике и Вселенной .
В одном лондонском пабе бармен записал для себя ISBN-номер «Современной 
Благодарности
511
космологии» Скотта Додельсона (Scott Dodelson, Modern Cosmology); в джа-
зовом клубе Green Mill в Чикаго я получил бесплатный напиток за то, что объ-
яснил, что такое темная энергия . Я хочу поблагодарить всех тех, кто, не будучи
ученым, все же продолжает интересоваться внутренними механизмами При-
роды, стремится задавать вопросы и размышлять над ответами . Изучение
природы времени, возможно, не поможет нам изобрести лучшие телевизоры
или научиться худеть без упражнений, но мы все живем в одной общей Вселен-
ной, и стремление понять ее — это часть того, что делает нас людьми . 
Ш. Кэрролл
Вечность. В поисках окончательной теории времени
Перевела с английского Е. Шикарева
Научный редактор Дмитрий Геннадиевич Левков,
научный сотрудник Института ядерных исследований РАН, кандидат физ.-мат. наук
Заведующая редакцией
Ведущий редактор
Литературный редактор
Художник
Корректор
Верстка
Ю. Сергиенко
Н. Римицан
О. Лапина
В. Шимкевич
Н. Викторова
Л. Егорова
ООО «Питер Пресс», 192102, Санкт-Петербург, ул. Андреевская (д. Волкова), 3, литер А, пом. 7Н.
Налоговая льгота — общероссийский классификатор продукции ОК 034-2014, 58.11.12.000 —
Книги печатные профессиональные, технические и научные.
Подписано в печать 18.12.15. Формат 60×90/16. Бумага офсетная. Усл. п. л. 32,000.
Тираж 3500. Заказ 0000.
Отпечатано в полном соответствии с качеством предоставленного электронного оригинал-макета
в типографии филиала АО «ТАТМЕДИА» «ПИК «Идел-Пресс».
420066, Казань, ул. Декабристов, 2. E-mail: idelpress@mail.ru








