Кривизна пространства
Представьте себе, что вы взяли карандаш и пытаетесь поставить его на кончик
грифеля . Очевидно, что он сразу же начнет падать . Но если бы в вашем рас-
поряжении была чрезвычайно устойчивая поверхность, а вы были бы настоящим
мастером балансировки, то вы бы могли установить эту конструкцию так,
чтобы карандаш оставался в вертикальном положении очень долгое время .
Скажем, более 14 миллиардов лет .
Этот пример хорошо иллюстрирует нашу Вселенную, а карандаш пред-
ставляет такую ее характеристику, как кривизна пространства. В действитель-
ности это не самое запутанное понятие, но космологи зачастую искусственно
усложняют его, говоря то о «кривизне пространства—времени», то о «кри- 
|
|
|
|
|
Глава 14 . Инфляция и Мультиленная
421
визне пространства» . Это разные вещи, и нам приходится каждый раз из
контекста догадываться, что именно имелось в виду . Так же как пространство—
время может обладать кривизной, кривизна может быть и у пространства само-
го по себе, и вопрос о том, искривлено ли пространство, абсолютно не связан
с вопросом искривленности пространства—времени .4
Одна из проблем, которые потенциально могут всплыть при обсуждении
кривизны пространства самого по себе, заключается в том, что общая теория
относительности предоставляет нам возможность нарезать пространство—вре-
мя на трехмерные копии эволюционирующего во времени пространства множе-
ством разных способов; определение «пространства» не уникально . К счастью,
в нашей наблюдаемой Вселенной существует естественный вариант подобной
нарезки: мы определяем «время» так, чтобы плотность материи оставалась при-
близительно одинаковой в пространстве на больших масштабах, но уменьшалась
по мере расширения Вселенной . Другими словами, распределение материи
определяет естественную покоящуюся систему координат во Вселенной . Это ни
в коем случае не нарушает принципы относительности, так как отражает свойства
одной конкретной конфигурации материи, а не базовые законы физики .
В целом пространство может совершенно произвольным способом ис-
кривляться в разных точках, и для того чтобы справиться с математикой, опи-
сывающей искривление, была разработана особая дисциплина, носящая на-
звание дифференциальной геометрии . Но космологам повезло: пространство
при рассмотрении очень больших расстояний является однородным и выглядит
одинаково во всех направлениях . В такой ситуации достаточно указать одно
значение — «пространственную кривизну», чтобы узнать все необходимое
о геометрии трехмерного пространства . Кривизна пространства может вы-
ражаться положительным числом, отрицательным числом или быть равной
нулю . Если кривизна равна нулю, то мы, естественно, говорим, что пространство
«плоское» и обладает всеми геометрическими характеристиками в привычном
для нас понимании . Эти характеристики впервые были сформулированы Эв-
клидом и включают такие свойства, как «параллельные линии никогда не пере-
секаются» и «сумма углов треугольника равна в точности 180 градусам» . Если
кривизна положительна, то пространство напоминает поверхность сферы, —
за исключением того, что оно трехмерно . Линии, параллельные на каком-то
участке, в конечном счете пересекутся, а сумма углов треугольника превышает
180 градусов . Если же кривизна отрицательная, то пространство похоже на
седло или картофельные чипсы . Линии, параллельные на каком-то участке,
расходятся в стороны, а сумма углов треугольника — ну, вы, вероятно, уже
догадались .5 
422
(
)
Часть IV . Из кухни в Мультиленную
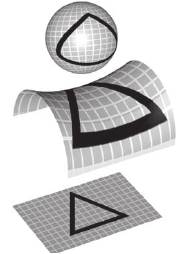
Рис . 14 .2 . Варианты пространств с постоянной кривизной . Сверху вниз: положительная
кривизна, как на сфере; отрицательная кривизна, как на седле; нулевая кривизна, как на плос-
кой поверхности
Согласно правилам общей теории относительности, если при рождении
Вселенная была плоской, то она остается плоской . Если она появилась в ис-
кривленном состоянии, то кривизна постепенно, по мере расширения Вселен-
ной, уменьшается . Однако, как мы уже знаем, плотность материи и излучения
также уменьшается . (Пока позабудьте даже о том, что вы когда-либо слышали
такой термин, как темная энергия, потому что она все ставит с ног на голову .)
Написав уравнения, можно убедиться, что плотность материи или излучения
уменьшается быстрее, чем вклад кривизны пространства . По сравнению с ма-
терией и излучением кривизна по мере расширения Вселенной оказывает все
большее влияние на эволюцию Вселенной .
Следовательно, если в ранней Вселенной присутствовал хоть сколько-нибудь
заметный вклад кривизны, сегодня искривленность Вселенной должна быть
очевидной . Плоская Вселенная подобна карандашу, поставленному на кончик
грифеля: малейшее отклонение влево или вправо моментально приведет к па-
дению карандаша . Схожим образом, любое мельчайшее отклонение от идеаль-
ной плоскостности в ранние годы должно с годами становиться все более
и более заметным . Но наблюдения показывают, что Вселенная выглядит очень
плоской . Насколько можно судить, никакой поддающейся измерению кривиз-
ны в современной Вселенной не наблюдается .6 
|
Глава 14 . Инфляция и Мультиленная
423
Такое состояние дел известно под названием проблемы плоскостности. Раз
Вселенная настолько плоская сегодня, она должна была быть невероятно пло-
ской и в прошлом . Но почему?
Проблема плоскостности имеет определенное сходство с проблемой эн-
тропии, которую мы разбирали в предыдущей главе . В обоих случаях загвоздка
не в ужасающем несоответствии между теорией и наблюдением — нам доста-
точно постулировать, что ранняя Вселенная пребывала в какой-то определен-
ной форме, и тогда головоломка прекрасно складывается . Проблема в том, что
«определенная форма» создает впечатление формы неестественной и при-
нудительно тонко подстроенной, причем без всяких очевидных на то причин .
Конечно, мы могли бы сказать, что и энтропия и пространственная кривизна
ранней Вселенной были малы, и на этом закончить историю безо всяких до-
полнительных объяснений . Но эти очевидно неестественные свойства Вселен-
ной могут быть ключом к чему-то важному, поэтому надлежит относиться к ним
со всей серьезностью .