Эта догадка получила название голографического принципа. Впервые данный
принцип был предложен нидерландским ученым, нобелевским лауреатом Ге-
рардом 'т Хоофтом и американским физиком-теоретиком, специалистом в об-
ласти теории струн Леонардом Сасскиндом, а позднее он был формализован
немецко-американским физиком Рафаэлем Буссо (бывшим учеником Стивена
Хокинга) .22 На первый взгляд голографический принцип может казаться не
слишком интересным . Хорошо, число возможных состояний в области про-
порционально размеру этой области в квадрате, а не ее размеру в кубе . Но это
совсем не тот тип замечаний, которые позволяют привлечь к себе внимание
и моментально очаровать незнакомцев на вечеринке .
Вот почему голография важна: этот принцип означает, что пространство—
время не фундаментально . Обычно, размышляя о происходящем во Вселенной,
мы неявно предполагаем существование чего-то вроде локальности; мы от-
дельно описываем то, что случилось здесь, и отдельно то, что случилось там, не
связывая между собой все возможные положения в пространстве . Голография
утверждает, что в принципе так делать нельзя, потому что еле уловимые связи
существуют между любыми событиями, происходящими в разных точках про-
странства, и это здорово ограничивает нашу свободу в описании конфигурации
материи в пространстве .
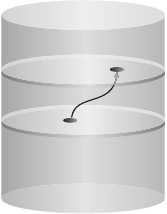
Обычная голограмма создает впечатление объемного изображения за счет
отражения света от особой двумерной поверхности . Голографический принцип
гласит, что на фундаментальном уровне Вселенная примерно такая же: все, что,
по нашему мнению, происходит в трехмерном пространстве, в действитель-
ности тайно закодировано на двумерной поверхности, насыщенной информа-
цией . Трехмерное пространство, в котором мы живем и дышим, можно было
бы (опять же в принципе) реконструировать, отталкиваясь от намного более 
372
Часть IV . Из кухни в Мультиленную
компактного описания . Доступ к этому описанию у нас может быть, а может
и отсутствовать . Второй вариант намного более вероятен, но в следующем
разделе мы детально рассмотрим пример ситуации, когда эта информация нам
доступна .
Возможно, ничто из этого вас не удивляет . Как мы говорили в предыдущей
главе, квантовой механике присущ определенный тип нелокальности даже без
учета гравитации; состояние Вселенной описывает все частицы скопом, не
ссылаясь на каждую конкретную частицу . Таким образом, когда в игру вступа-
ет гравитация, вполне естественно предполагать, что состояние Вселенной
будет включать все пространство—время сразу . И все же тип нелокальности,
подразумеваемый голографическим принципом, отличается от нелокальности
квантовой механики как таковой . В квантовой механике можно вообразить
такие волновые функции, в которых состояние кошки запутано с состоянием
собаки, но точно так же можно вообразить состояния, которые вообще не за-
путаны между собой, или же состояния, запутанность которых принимает
какую-то другую форму . В то же время голографический принцип утверждает,
что есть процессы, которые попросту не могут происходить, что информация,
необходимая для описания мира, может быть сжата во много раз . Следствия,
вытекающие из этой идеи, по сей день до конца не изучены, и можно не со-
мневаться, что впереди нас ждет еще очень много сюрпризов .
Хокинг сдается
Голографический принцип — очень общая идея; он должен быть частью теории
квантовой гравитации, какой бы она ни оказалась, которая в итоге будет при-
знана верной . А нам хотелось бы иметь возможность рассмотреть какой-нибудь
конкретный пример, демонстрирующий следствия голографического принци-
па . Например, мы думаем, что энтропия черной дыры в нашем обычном трех-
мерном пространстве пропорциональна двумерной площади ее горизонта
событий . Значит, в принципе мы могли бы описать все возможные микросо-
стояния этой черной дыры в терминах различных величин, заданных на этой
двумерной поверхности . Это цель многих физиков-теоретиков, работающих
в области квантовой гравитации, но, к сожалению, пока мы не знаем, как ее
достичь .
В 1997 году физик-теоретик Хуан Малдасена, американец аргентинского
происхождения, перевернул с ног на голову наше понимание квантовой гра-
витации, обнаружив явный пример голографии в действии .23 Он рассматривал
гипотетическую Вселенную, совершенно непохожую на нашу: в ней, как ми- 
Глава 12 . Черные дыры: конец времени
373
нимум, энергия вакуума была отрицательной (тогда как в нашей она представ-
ляется положительной) . Поскольку пустое пространство с положительной
энергией вакуума называется пространством де Ситтера, пустое пространство
с отрицательной энергией вакуума удобно называть «пространством анти-
де Ситтера» . Кроме того, Малдасена рассматривал пять измерений вместо
наших обычных четырех . И наконец, он работал в рамках очень специфической
теории гравитации и материи — «супергравитации», представляющей собой
суперсимметричную версию общей теории относительности . Суперсимме-
трия — это гипотетическая симметрия между бозонами (частицами силы)
и фермионами (частицами материи), играющая критически важную роль во
многих теориях современной физики элементарных частиц; к счастью, подоб-
ные детали не так важны для наших текущих целей .
Малдасена обнаружил, что эта теория — супергравитация в пятимерном
пространстве анти-де Ситтера — полностью эквивалентна абсолютно другой
теории — четырехмерной теории квантового поля, вообще без гравитационно-
го взаимодействия. Голография в действии: у всего, что только может произой-
ти в этой конкретной пятимерной теории с гравитацией, есть полный аналог
в теории без гравитации и без одного пространственного измерения . Мы го-
ворим, что эти теории «дуальны» по отношению друг к другу, — это означает,
что они совершенно не похожи внешне, но описывают одно и то же . Словно
у нас есть два разных, но при этом эквивалентных языка, и Малдасена нашел
розеттский камень, позволяющий переводить тексты с одного языка на другой
и обратно . Между состояниями той частной теории гравитации в пяти изме-
рениях и конкретной негравитирующей теории в четырех измерениях суще-
ствует взаимно-однозначное соответствие . Зная состояние в одной из них, мы
можем перевести его на язык другой, и, подчиняясь уравнениям движения для
каждой из рассматриваемых теорий, эти состояния эволюционируют в новые,
также соответствующие друг другу согласно тому же словарю (по крайней
мере, в принципе; на практике мы можем провести вычисления для простых
примеров, но более сложные ситуации пока нам не покоряются) . Очевидно,
что данное соответствие обязано быть нелокальным; невозможно соотнести
отдельные точки в четырехмерном пространстве с точками в пятимерном про-
странстве . Но можно представить, каким образом состояния в одной теории,
определенные в какой-то момент времени, будут соотноситься с состояниями
в другой теории .
Если это не убеждает вас, что пространство—время не фундаментально,
то даже представить не могу, какие еще доказательства вам требуются . У нас
есть явный пример двух разных версий одной и той же теории, описывающих 
374
—
Часть IV . Из кухни в Мультиленную
(
)
(
-
)
Рис . 12 .7 . Соответствие Малдасены . Теория гравитации в пятимерном пространстве анти-
де Ситтера эквивалентна теории без гравитации в четырехмерном плоском пространстве—
времени
пространство—время с разным числом измерений! Ни одна из этих теорий не
может считаться «единственно верной»; они полностью эквивалентны друг
другу .
Благодаря открытию Малдасены Стивен Хокинг согласился признать свое
поражение в споре с Прескиллом и Торном (хотя до этого, по обыкновению,
провел все вычисления своим способом, для того чтобы окончательно во всем
удостовериться) . Вспомните, что главный вопрос заключался в том, уничтожа-
ет ли информацию процесс испарения черной дыры (в отличие от эволюции
в соответствии с обычными правилами квантовой механики) или же информа-
ция, попадающая в черную дыру, каким-то образом уносится хокинговским
излучением .
Если Малдасена прав, то мы можем рассмотреть этот вопрос в контексте
пятимерного пространства анти-де Ситтера . Это не реальный мир, но детали,
отличающие его от реального мира, не связаны с загадкой потери информации;
в частности, можно вообразить, что отрицательная космологическая постоян-
ная очень мала и, по сути, не играет никакой роли . Итак, мы создаем черную
дыру в пространстве анти-де Ситтера и позволяем ей испаряться . Теряется ли
при этом информация? Давайте переведем этот вопрос на язык аналогичной
ситуации в четырехмерной теории . В этой теории гравитация отсутствует, и,
следовательно, все подчиняется правилам обычной квантовой механики . Од-
нако в четырехмерной негравитационной теории информация попросту не 











|
Глава 12 . Черные дыры: конец времени
375
может теряться, а раз теории эквивалентны, то и в пятимерной теории с гра-
витацией дела с информацией должны обстоять точно так же . Итак, если мы
не упустили какую-то критическую мелочь, информация должна каким-то
образом сохраняться в процессе испарения черной дыры .
Это основная причина, почему Хокинг признал поражение в споре и теперь
согласен с тем, что черные дыры не разрушают информацию . Но вы видите,
что это доказательство, хотя и кажется довольно основательным, все же явля-
ется косвенным . В частности, оно не предоставляет никакого конкретного
физического понимания того, каким образом информация попадает в хокин-
говское излучение . Очевидно, что это как-то происходит, но каков конкретный
механизм — пока неясно . Вот почему Торн со своим проигрышем в споре не
согласился, а Прескилл неохотно принял причитающуюся ему энциклопедию .
Независимо от того, соглашаемся мы с утверждением о сохранении информа-
ции или нет, ясно одно: ученым еще предстоит серьезно поработать, чтобы
выяснить, что же именно происходит при испарении черной дыры .