Сколько состояний поместится в контейнер?
Мы неспроста пытаемся докопаться до самой сути черных дыр в книге, которая,
по идее, должна быть посвящена стреле времени: стрела времени связана
с увеличением энтропии, а главная причина этого увеличения кроется в низкой
энтропии сразу после Большого взрыва — в тот период истории Вселенной,
когда гравитация играла принципиально важную роль . Таким образом, нам
необходимо знать, как энтропия ведет себя в присутствии гравитации, и не-
полное понимание квантовой гравитации сдерживает нас, не давая добраться
до сути . Единственный намек, которым мы располагаем, — это формула Хо-
кинга для энтропии черной дыры; попробуем воспользоваться этой подсказкой
и посмотрим, куда это нас приведет . Действительно, попытки понять энтропию
черной дыры и разобраться с парадоксом о потере информации в черных дырах
существенно продвинули исследования пространства—времени и пространства
состояний в квантовой гравитации .
Рассмотрим такую загадку: сколько энтропии может уместиться в контей-
нере? Больцману и его современникам этот вопрос показался бы глупым — ведь
в коробку можно вместить столько энтропии, сколько душа пожелает . Если
у нас есть контейнер, полный молекул газа, то состояние с максимальной эн-
тропией (равновесная конфигурация) будет существовать для любого фикси-
рованного числа молекул — газ будет равномерно распределен по контейнеру
при постоянной температуре . При желании мы могли бы впихнуть в этот
контейнер еще больше энтропии; все, что нам для этого потребовалось бы, —
это добавить больше молекул . Если нас вдруг начнет волновать вопрос о том,
что молекулы занимают определенный объем пространства и существует некое 
368
Часть IV . Из кухни в Мультиленную
максимальное число молекул, которые могут поместиться в контейнер, то и эту
проблему мы сможем без труда решить, взяв контейнер, полный фотонов (частиц
света), а не молекул газа . Фотоны можно нагромождать друг на друга беско-
нечно, и мы сможем уместить в контейнере столько фотонов, сколько нам по-
требуется . С этой точки зрения ответ вроде бы таков, что в любой конкретный
контейнер можно уместить бесконечный (или, по крайней мере, произвольно
большой) объем энтропии .
В этой истории, однако, отсутствует критически важный ингредиент: грави-
тация . Мы вталкиваем в контейнер все больше вещества, и масса содержимого
контейнера возрастает .20 В конце концов материю, которую мы засовываем
в контейнер, ожидает та же судьба, что и массивную звезду, израсходовавшую
свое ядерное топливо: она сколлапсирует под воздействием собственного гра-
витационного притяжения и превратится в черную дыру . Каждый раз, когда это
происходит, энтропия увеличивается — энтропия черной дыры больше, чем
энтропия материи, из которой она была сделана (в противном случае второй
закон термодинамики не позволил бы черным дырам образовываться) .
В отличие от контейнеров с атомами создавать черные дыры одинакового
размера, но с разными массами невозможно . Размер черной дыры характери-
зуется радиусом Шварцшильда, в точности пропорциональным ее массе .21 Если
вам известна масса, то вы знаете размер; и наоборот, если у вас имеется кон-
тейнер фиксированного размера, то вы не сможете запихнуть в него черную
дыру тяжелее определенной массы . Но если энтропия черной дыры пропор-
циональна площади ее горизонта событий, это означает, что существует мак-
симальный объем энтропии, который может уместиться в области какого-то
фиксированного размера, что обеспечивается черной дырой этого размера.
Это весьма примечательный факт . Он отражает разительное отличие, появ-
ляющееся в поведении энтропии, как только влияние гравитации становится
существенным . В гипотетическом мире, в котором такой штуки, как гравитация,
не существует, мы могли бы втиснуть сколько угодно энтропии в любую заданную
область, но в реальном мире гравитация не позволяет нам это сделать .
Значимость этого результата становится очевидной, когда мы обращаемся
к больцмановскому пониманию энтропии как (логарифма) числа микрососто-
яний, неразличимых с макроскопической точки зрения . Если существует какой-
то конечный максимальный объем энтропии, который может уместиться
в области фиксированного размера, значит, данная область допускает лишь
конечное число возможных состояний . Это фундаментальное свойство кван-
товой гравитации, кардинально отличное от свойств теорий, не включающих
гравитацию . Посмотрим, куда эта цепочка рассуждений нас приведет . 
Глава 12 . Черные дыры: конец времени
369
Голографический принцип
Для того чтобы оценить, насколько серьезный урок преподает нам энтропия
черных дыр, необходимо сначала прочувствовать глубину почитаемого многи-
ми принципа, который черные дыры со своей энтропией, очевидно, опровер-
гают, — локальности. Его основная идея заключается в том, что разные места
во Вселенной функционируют более или менее независимо друг от друга . На
объект, находящийся в каком-то конкретном месте, может воздействовать его
ближайшее окружение, но не то, что находится очень и очень далеко . Пред-
меты, разнесенные на большое расстояние, могут влиять друг на друга косвен-
ным образом, отправляя из одного место в другое какие-то сигналы, например
возмущение гравитационного поля или электромагнитную волну (свет) . Од-
нако то, что происходит здесь, не оказывает непосредственного влияния на то,
что происходит в какой-то другой области Вселенной .
Вспомним снова шахматные доски . На событие, происходившее в опреде-
ленный момент времени, влияло событие, происшедшее моментом ранее . Но
то, что происходило в определенной точке «пространства» (совокупности
клеток в пределах одной строки), никак не было связано с происходящим
в любой другой точке пространства в тот же момент времени . В любой кон-
кретной строке у нас могло быть абсолютно любое распределение белых
и серых квадратиков . Никаких правил типа «если здесь находится серая клет-
ка, то через двадцать мест направо должна находиться белая» не существова-
ло . Да, по ходу времени клетки «взаимодействовали» друг с другом, но взаи-
модействие всегда ограничивалось соседними клетками . Схожим образом,
в реальном мире объекты сталкиваются друг с другом и воздействуют на
другие объекты, находящиеся поблизости, но не где-то далеко . Это локальность .
Локальность приводит к важному следствию для энтропии . Возьмем, как
обычно, контейнер с газом и подсчитаем энтропию газа в контейнере . Теперь
мысленно поделим контейнер на две части и вычислим энтропию в каждой
половине . (Не нужно воображать физический барьер, просто рассматривайте
левую и правую половины контейнера по отдельности .) Как связаны между
собой полная энтропия контейнера и энтропии двух половин, взятые отдельно?
Ответ таков: энтропию целого контейнера можно получить, просто сложив
энтропию одной его половины с энтропией другой его половины . Казалось
бы, это непосредственно следует из определения энтропии по Больцману —
собственно, поэтому в данном определении и присутствует логарифм . У нас
есть определенное количество допустимых микросостояний в одной половине
контейнера и определенное количество допустимых микросостояний в другой . 
370
Часть IV . Из кухни в Мультиленную
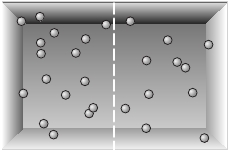
Рис . 12 .6 . Контейнер с газом, мысленно поделенный на две половины . Полная энтропия
содержимого контейнера равна сумме энтропий двух половин содержимого
Общее количество микросостояний рассчитывается так: для каждого возмож-
ного микросостояния левой половины мы можем выбрать любое из возможных
состояний правой половины . Таким образом, мы получаем общее количество
микросостояний путем умножения числа микросостояний слева на число микро-
состояний справа . Но энтропия — это логарифм полученного значения, а ло-
гарифм «X умноженного на Y» равен «логарифм X» плюс «логарифм Y» .
Итак, энтропия всего контейнера равна простой сумме энтропий двух по-
ловин . И это правило будет работать независимо от того, каким образом мы
разделим исходный контейнер и на сколько частей; полная энтропия системы
всегда равна сумме энтропий подсистем . Это означает, что максимальная воз-
можная для выбранного контейнера энтропия всегда будет пропорциональна
его объему: чем больше у нас пространства, тем большее значение может при-
нимать энтропия, так что она естественным образом масштабируется с увели-
чением объема .
Однако обратите внимание на коварное предположение, присутствующее
в этом рассуждении: мы подсчитали количество состояний в одной половине
контейнера, а затем умножили его на количество состояний в другой половине .
Другими словами, предполагалось, что то, что происходило в одной половине
контейнера, никак не зависело от происходящего в другой его половине . А это
как раз предположение о локальности .
Когда на сцену выходит гравитация, все эти доводы рушатся . Гравитация
устанавливает верхний предел на энтропию, которую мы можем впихнуть
в контейнер, равный энтропии самой большой черной дыры, способной по-
меститься в данную тару . Однако энтропия черной дыры не пропорциональна
заключенному в ней объему — она пропорциональна площади горизонта со-
бытий . А площадь может очень сильно отличаться от объема! Если у нас есть 
|
Глава 12 . Черные дыры: конец времени
371
сфера диаметром один метр и мы увеличим ее в размере так, чтобы ее диаметр
возрос до двух метров, то внутренний объем сферы возрастет в восемь раз (23),
тогда как площадь ее поверхности возрастет лишь в четыре раза (22) .
Вывод прост: квантовая гравитация не подчиняется принципу локальности .
В квантовой гравитации происходящее здесь не может быть абсолютно неза-
висимым от происходящего там . Максимальное количество вещей, которые
могут происходить в какой-то области пространства (число возможных микро-
состояний в ней), не пропорционально объему этой области; оно пропорцио-
нально площади поверхности границы данной области . В реальном мире, ко-
торый описывает квантовая гравитация, в заданную область получается втиснуть
намного меньше информации, чем мы могли бы наивно предполагать, не беря
в расчет гравитацию .