Полезная и бесполезная энергия
У нашего примера с контейнером газа есть интересная особенность: стрела
времени там — явление временное . После того как концентрация газа вы-
равнивается (примерно в момент времени t = 150 на рис . 8 .3), ничего боль-
ше не происходит . Отдельные молекулы продолжают перелетать из левой
половины в правую и обратно, но число таких молекул взаимно компенсиру-
ется, и большую часть времени количество молекул слева и справа будет
одинаково . Это конфигурации, соответствующие наибольшему числу рас-
становок отдельных молекул, в которых система соответственно обладает
наибольшей энтропией .
Система, обладающая максимально возможной энтропией, находится
в равновесии. Когда наступает состояние равновесия, системе становится не-
куда двигаться дальше; такая конфигурация для нее наиболее естественна .
В равновесной системе стрела времени отсутствует, так как энтропия не уве-
личивается (и не уменьшается) . Для макроскопического наблюдателя система
в равновесии предстает статичной, не меняющейся .
Ричард Фейнман в своей лекции «Характер физических законов» расска-
зывает историю, иллюстрирующую концепцию равновесия .8 Представьте себе,
что вы сидите на пляже и внезапно на вас обрушивается ливень . Вы принесли
с собой полотенце, но пока вы успеваете добежать до укрытия, оно также про-
мокает . Оказавшись под крышей, вы начинаете вытираться полотенцем . Какое-
то время это работает, потому что полотенце промокло чуть меньше, чем вы .
Тем не менее вскоре вы обнаруживаете, что оно пропиталось влагой и вы,
вытираясь им, настолько же быстро смачиваете свою кожу, насколько быстро
стираете с нее капли воды . Вы с полотенцем достигли состояния «равновесия
влажности», и оно уже не может высушить вас . Это состояние, в котором
число способов разместить молекулы воды на вас и на вашем полотенце мак-
симально .9
После достижения состояния равновесия полотенце становится непри-
годным для достижения первоначальной цели (обсушиться) . Обратите внима-
ние, что когда вы вытираетесь, полный объем воды не меняется — она просто
переходит с вас на полотенце . Аналогично, в контейнере с газом, изолирован-
ном от внешнего мира, полная энергия не меняется; она остается постоянной,
по крайней мере в ситуациях, когда расширением пространства можно пре-
небречь . Однако энергия может быть распределена так, чтобы приносить
какую-то пользу, а может быть и бесполезной . Когда энергия находится в кон-
фигурации с низкой энтрпией, ее можно использовать для совершения работы . 
212
Часть III . Энтропия и ось времени
Но тот же объем энергии в состоянии равновесия абсолютно бесполезен .
Энтропия — это также мера бесполезности конфигурации энергии .10
Снова вернемся к нашему контейнеру с перегородкой . Но на этот раз пусть
это будет не перегородка с отверстием, жестко зафиксированная внутри кон-
тейнера и лишь позволяющая некоторой части молекул пролетать из одной его
половины в другую, а сплошная подвижная пластина, прикрепленная к стерж-
ню, выходящему за пределы контейнера . То, что мы сейчас описали, — всего
лишь обыкновенный поршень, с помощью которого при определенных обсто-
ятельствах можно производить работу .
На рис . 8 .4 показаны две разные ситуации, в которых может оказаться наш
поршень . Вверху проиллюстрирована конфигурация с низкой энтропией: все
молекулы газа находятся с одной стороны от перегородки . Внизу изображена
ситуация с высокой энтропией: с обеих сторон от перегородки находятся
равные объемы газа . Полное количество молекул и полная энергия одинаковы
в обоих случаях; отличается только энтропия . Также очевидно, что развивать-
ся события в этих двух случаях будут совершенно по-другому . В случае, пред-
ставленном в верхней части рисунка, весь газ находится с левой стороны от
поршня . Сила молекул, ударяющихся о перегородку, оказывает давление, ко-
торое выталкивает поршень до тех пор, пока газ не заполнит весь объем кон-
тейнера . Подвижный стержень поршня можно использовать для выполнения
полезной работы, например кручения маховика (по крайней мере, в течение
какого-то небольшого промежутка времени) . При этом расходуется энергия
газа, поэтому в конце процесса его температура станет ниже . (Поршни в дви-
гателе вашего автомобиля работают точно так же, расширяя и охлаждая горячие
газы — продукты сгорания паров бензина; эта полезная работа и приводит
автомобиль в движение .)
В нижней части рисунка показан процесс, в котором первоначальная энер-
гия такая же, но энтропия намного выше: по обеим сторонам перегородки
находится одинаковое количество частиц . Высокая энтропия подразумевает
равновесие, что, в свою очередь, свидетельствует о бесполезности энергии .
И действительно, мы видим, что поршень не движется . Давление газа с одной
стороны перегородки компенсируется давлением с другой стороны . Полная
энергия газа в этом контейнере равна полной энергии в контейнере, изобра-
женном в левом верхнем углу, однако в данном случае мы не можем воспользо-
ваться ею в своих целях, например заставить газ передвинуть поршень и помочь
нам сделать что-то полезное .
Этот пример помогает нам понять связь между взглядом Больцмана на
энтропию и мнением Рудольфа Клаузиуса, который впервые сформулировал 
Глава 8 . Энтропия и беспорядок
213
Рис . 8 .4 . Газ в разделенном сплошной перегородкой контейнере, применяемый для при-
ведения в движение поршня . Вверху газ в состоянии с низкой энтропией выталкивает
поршень вправо, производя полезную работу . Внизу газ в состоянии с высокой энтропией
никак не влияет на положение поршня
второе начало термодинамики . Вспомните, что Клаузиус и его предшествен-
ники вообще не думали об энтропии в терминах атомов, они рассматривали ее
как независимую субстанцию с собственной динамикой . В исходной версии
второго начала термодинамики энтропия даже не упоминалась; это было все-
го лишь утверждение о том, что «теплота не может спонтанно начать течь от
более холодного объекта к более горячему» . Когда контактируют два объекта
с разной температурой, их температуры постепенно изменяются по направле-
нию к некоторому равновесному значению между ними . Если же в контакте
находятся два объекта с одинаковой температурой, то с ними ничего не про-
исходит (так как они уже находятся в температурном равновесии) .
С точки зрения физики атомов все это также имеет смысл . Возьмем клас-
сический пример соприкосновения двух объектов с разной температурой:
кубик льда в стакане теплой воды (о котором мы говорили в конце прошлой
главы) . И кубик льда, и жидкость состоят из совершенно одинаковых молекул,
а именно H2O . Единственное различие заключается в том, что температура льда
намного ниже . Как мы уже говорили выше, температура — это мера средней
энергии движения молекул в веществе . Таким образом, молекулы жидкой воды
двигаются относительно быстро, а молекулы льда — медленно .
Однако такой тип условий — два набора молекул, в одном из которых моле-
кулы движутся быстро, а в другом медленно, концептуально почти не отличает-
ся от двух наборов молекул, заключенных в контейнере по разные стороны от
перегородки . В любом случае присутствуют макроскопические ограничения на 
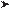
|
|
|
|
214
Часть III . Энтропия и ось времени
перестановки микроскопических частей этих систем . Если бы у нас был только
стакан воды, имеющей постоянную температуру, мы могли бы заменять молеку-
лы в одной части стакана молекулами из какой-то другой его части, и с макроско-
пической точки зрения никаких различий при этом мы бы не увидели . Но если
в воде плавает кубик льда, то нельзя запросто поменять местами молекулы льда
и молекулы обычной воды — при этом кубик льда начал бы двигаться, и мы за-
метили бы это даже со своей макроскопической точки зрения . Деление молекул
воды на «жидкость» и «лед» накладывает серьезные ограничения на число
доступных перестановок, поэтому данная конфигурация обладает низкой эн-
тропией . По мере того как температура молекул воды, составлявших в начале
эксперимента ледяной кубик, и температура «жидкой» воды в стакане вырав-
ниваются, энтропия возрастает . Правило Клаузиуса о тенденции к выравниванию
температур и о том, что теплота не может спонтанно течь от холодного объекта
к горячему, абсолютно эквивалентно утверждению, что энтропия, как ее опре-
делил Больцман, в замкнутой системе никогда не уменьшается .
Ничто из этого, разумеется, не означает, что охладить объект невозможно .
Однако в повседневной жизни с учетом того, что большинство вещей вокруг
нас имеют одинаковую температуру, это требует большей изобретательности,
чем нагревание . Холодильник — куда более сложное устройство, чем плита
(работа холодильника основывается на том же базовом принципе, что и рабо-
та поршня, показанного на рис . 8 .4: двигатель устройства расширяет газ, за-
бирая у него энергию и таким образом охлаждая его) . Когда Гранту Ачатцу,
шеф-повару чикагского ресторана «Alinea», потребовалось устройство, кото-
рое умело бы быстро охлаждать продукты — точно так же, как поставленная
на огонь сковорода мгновенно нагревает их, для создания такой машины ему
пришлось объединить усилия с Филипом Престоном, технологом, специали-
зирующемся на кухонном оборудовании . Результатом их совместной работы
стала «антисковорода» — устройство размером с микроволновую печь, ме-
таллическая верхняя поверхность которого имеет температуру –34 °С . Если
вылить на эту «антисковороду» горячее пюре или соус, то нижний его слой
мгновенно замерзнет, а верхняя часть останется мягкой . Мы уже давно усвои-
ли основы термодинамики, но продолжаем изобретать новые способы при-
менения науки для облегчения собственной жизни .
Не зацикливайтесь на деталях
В пятницу вечером вы выбрались с друзьями в клуб поиграть в бильярд . Сейчас
мы говорим о бильярде из реального мира, а не о «бильярде физиков», в кото- 
Глава 8 . Энтропия и беспорядок
215
ром мы пренебрегаем трением и шумом .11 Один из ваших друзей только что
эффектно разбил пирамиду . Раскатившиеся по столу шары остановились, вы
принялись обдумывать свой следующий удар, и вдруг проходящий мимо не-
знакомец восклицает: «Ух ты! Это невероятно!»
В недоумении вы спрашиваете, что же тут невероятного, и слышите в ответ:
«Вы только посмотрите: все эти шары оказались ровно в этих точках на столе!
Какова вероятность того, что вам когда-либо удастся расположить их в точ-
ности таким же образом? Да вы не сможете повторить этого и за миллион лет!»
От загадочного незнакомца попахивает безумием — наверное, он немного
свихнулся, читая слишком много философских трактатов об основах статисти-
ческой механики . Однако в его словах есть определенный смысл . На столе
с несколькими шарами появление любой заданной конфигурации крайне мало-
вероятно . Представьте, что вы запустили биток в группу случайным образом
расставленных по столу шаров, а они, покатавшись туда-сюда, остановились
ровно в тех же точках, в которых находились до удара . Увидев такое, вы были
бы поражены до глубины души! Однако вероятность данной конфигурации
(конечные положения в точности совпадают с начальными) не больше и не
меньше вероятности любого другого расположения шаров на столе .12 Имеем
ли мы право выделять ее на фоне других, называя «поразительной» или «не-
вероятной», а все остальные именовать «непримечательными» или «случай-
ными»?
Этот пример превосходно иллюстрирует центральный вопрос больцманов-
ского определения энтропии и понимания второго начала термодинамики: кто
решает, можно ли считать два данных микроскопических состояния системы
одинаковыми с нашей, макроскопической, точки зрения?
Формула для энтропии, выведенная Больцманом, основывается на величи-
не W, которую мы определили как «количество способов разместить микро-
скопические составляющие системы так, чтобы ее макроскопический образ не
изменился» . В предыдущей главе мы определили «состояние» физической
системы как полный набор информации, необходимой для однозначного опи-
сания ее движения с течением времени; в классической механике это положения
и импульсы всех составляющих систему частиц . Теперь, когда мы рассматрива-
ем статистическую механику, удобно использовать термин «микросостояние»,
подразумевая точное состояние системы, в противоположность «макрососто-
янию», включающему лишь те характеристики, которые поддаются наблюдению
с макроскопической точки зрения . В этом случае можно дать величине W
краткое определение: число микросостояний, соответствующих данному ма-
кросостоянию . 
216
Часть III . Энтропия и ось времени
Для контейнера с газом, разделенного перегородкой на две половины,
микросостоянием в любой момент времени является список положений и им-
пульсов всех молекул газа . Однако нас интересовало только, сколько молекул
находится слева от перегородки, а сколько — справа . Неявным образом каждый
вариант деления группы молекул на части — сколько-то слева, а оставшиеся
справа — определял «макросостояние» контейнера . А когда мы вычисляли
значения W, мы всего лишь подсчитывали количество микросостояний, соот-
ветствующих данному макросостоянию .13
Раньше решение не отслеживать ничего, кроме количества молекул в каждой
половине контейнера, казалось нам совершенно безобидным . Но мы могли бы
следить и за массой других параметров . Имея дело с атмосферой в настоящей
комнате, мы можем учитывать намного больше параметров, чем просто коли-
чество молекул в каждой части помещения: например, отслеживать темпера-
туру, плотность и атмосферное давление в каждой точке комнаты или, по
крайней мере, в некотором наборе точек . Если в атмосфере содержится смесь
газов, то мы могли бы по отдельности следить за плотностью и другими пара-
метрами каждого из газов . В любом случае, объем информации, которым нам
пришлось бы при этом манипулировать, все равно был бы намного меньше, чем
если бы мы записывали положения и импульсы всех молекул в комнате . Тем не
менее процедура выбора, какую информацию относить к макроскопическим
характеристикам, а какую отбрасывать как несущественную составляющую
микросостояния, определена недостаточно четко .
Процесс деления пространства микросостояний какой-то физической систе-
мы (газ в контейнере, стакан воды или Вселенная) на наборы, которые мы по-
мечаем как «макроскопически неразличимые», называется «огрублением» . Это
такая черная магия, играющая критически важную роль в наших рассуждениях
об энтропии . Рисунок 8 .5 демонстрирует, как она работает: мы всего лишь делим
пространство всех состояний системы на области (макросостояния), которые
с точки зрения макроскопического наблюдателя кажутся одинаковыми . Каждая
точка внутри любой такой области соответствует одному из микросостояний,
а энтропия, связанная с данным микросостоянием, пропорциональна логарифму
площади этой области, которому это микросостояние принадлежит (в действи-
тельности не площади, а объема, так как мы говорим о чрезвычайно многомерном
пространстве) . При взгляде на подобную схему становится очевидно, почему
энтропия имеет тенденцию к увеличению: как правило, система развивается по
направлению от состояний с низкой энтропией, соответствующих крошечной
части пространства состояний, к состояниям из объемных областей, с которыми
связаны большие значения энтропии . 
Глава 8 . Энтропия и беспорядок
217
Рис . 8 .5 . Процедура огрубления представляет собой разделение пространства всех воз-
можных микросостояний на области, считающиеся неразличимыми с макроскопической
точки зрения, — макросостояния . С каждым макросостоянием связано значение энтропии,
пропорциональное логарифму объема этого макросостояния в пространстве состояний .
Размер областей с низкой энтропией увеличен в целях наглядности; в действительности они
чрезвычайно малы по сравнению с областями с высокой энтропией
Рисунок 8 .5 не масштабирован; если бы мы хотели представить реальную
систему, то макросостояния с низкой энтропией занимали бы намного меньшую
площадь по сравнению с площадью, отведенной под макросостояния с высокой
энтропией . Как мы убедились на примере с поделенным на две части контей-
нером, количество микросостояний, соответствующих макросостояниям
с высокой энтропией, куда больше количества микросостояний, определяющих
макросостояния с низкой энтропией . Нет ничего удивительного в том, что
система с низкой начальной энтропией перейдет в более объемные области
пространства состояний, к макросостояниям с высокой энтропией . Если же
вначале система обладает высокой энтропией, то она может очень долго блуж-
дать по пространству состояний, не встречая при этом областей с низкой эн-
тропией . Вот что мы имеем в виду, говоря, что система находится в равновесии:
она не находится в статическом микросостоянии, просто никогда не выходит
из области, соответствующей макросостоянию с высокой энтропией .
Все эти рассуждения могут показаться вам нелепыми . Два микросостояния
принадлежат одному и тому же макросостоянию, если они макроскопически
неразличимы . Но это всего лишь один из способов сказать: «…когда мы не
можем отличить одно от другого, основываясь на своих макроскопических 
|
218
Часть III . Энтропия и ось времени
наблюдениях» . Именно это «мы» и должно вызывать у вас тревогу . Почему
вообще мы приплели сюда какие-то свои способности? Мы говорим об энтро-
пии как о характеристике всего мира, а не как об одной из сторон нашего умения
воспринимать мир . Два стакана воды находятся в одном и том же макрососто-
янии, если весь объем воды в них имеет одинаковую температуру, даже если
распределения положений и импульсов молекул воды в них отличаются, по-
тому что мы не можем непосредственно измерить эти величины . Однако пред-
ставьте себе, что нам встретилась раса супернаблюдательных инопланетян,
способных впериться взором в толщу воды и увидеть положения и импульсы
каждой заключенной там молекулы . Неужели эта раса вправе будет заявить, что
энтропии вообще не существует?
Ученые, работающие в области статистической механики, пока что не при-
знали единственно верным ни один из возможных ответов на озвученные выше
вопросы (если бы это произошло, то мы бы только его и рассматривали) . Да-
вайте обсудим пару мнений .
Прежде всего, многие считают, что это вообще не важно . То есть вам-то
может быть очень даже важно, как именно вы будете объединять микрососто-
яния в макросостояния в целях какой-то конкретной актуальной для вас физи-
ческой задачи, но в конечном итоге не имеет значения, как вы сделаете это, если
единственная ваша цель — доказать истинность какого-то утверждения вроде
второго начала термодинамики . Если посмотреть на рис . 8 .5, станет понятно,
почему второе начало термодинамики работает: в пространстве состояний
гораздо больший объем отведен под состояния с высокой энтропией, чем
с низкой, поэтому если мы начнем путешествие из последнего состояния, нет
ничего удивительного в том, что в итоге мы окажемся в первом . Однако так
будет всегда, независимо от того, как мы отсортируем микросостояния . Второе
начало термодинамики непоколебимо; оно зависит от определения энтропии
как логарифма от некоего объема внутри пространства состояний, но не от
точного способа выбрать этот объем . Как бы то ни было, на практике из мно-
жества альтернатив мы выбираем что-то одно, поэтому такая прозрачная по-
пытка избежать прямого ответа не может нас полностью удовлетворить .
Второе мнение заключается в том, что выбор — как именно провести
огрубление — не может быть абсолютно произвольным и зависящим от чело-
века, даже если без определенной степени предвзятости не обойтись . Действи-
тельно, мы сортируем микросостояния естественным, на наш взгляд, образом,
учитывая реальные физические условия, а не собственные прихоти . Например,
наблюдая за температурой и давлением в стакане воды, мы отбрасываем ту
информацию, получить которую можно лишь путем изучения содержимого 
Глава 8 . Энтропия и беспорядок
219
данного стакана под микроскопом . Мы определяем средние свойства в отно-
сительно небольших областях пространства, потому что так работают наши
органы чувств . Определившись с доступными критериями огрубления, мы
получаем относительно хорошо определенный набор поддающихся макроско-
пическому наблюдению величин .
Усреднение величин в небольших областях пространства — это не случай-
ный метод и не специфическая особенность функционирования человеческих
органов чувств в противоположность органам чувств гипотетических ино-
планетян . Это совершенно естественный подход с учетом того, как работают
законы физики .14 Когда я среди нескольких чашек кофе отмечаю те, куда только
что вылили ложку молока, и те, в которых молоко уже хорошенько перемешали
с основным содержимым, мои решения, к какой категории «состояний кофе»
отнести ту или иную чашку, не случайны; я руководствуюсь тем, как кофе, с моей
точки зрения, выглядит — непосредственно и феноменологически . Итак, даже
если, в принципе, наш подход к огрублению микросостояний в макросостояния
кажется абсолютно произвольным, в действительности мудрая природа одари-
ла нас умением делать это правильно и разумно .