Angelopoulos, A. et al . (CPLEAR Collaboration) . First Direct Observation of Time Reversal
Noninvariance in the Neutral Kaon System // Physics Letters, 1998, B 444, p . 43–51 . Группа
KTeV из лаборатории Fermilab под Чикаго провела похожий эксперимент . Его целью
также была оценка с помощью нейтральных каонов инвариантности относительно об-
ращения времени, но выполнен он был немного другим способом (Alavi-Harati, A. et al .
(KTeV Collaboration) . Observation of CP Violation in KL → π+π-e+e- Decays // Physical Review
Letters, 2000, 84, p . 408–411) .
Процитировано из работы Maglich, B . Adventures in Experimental Physics, Gamma
Volume . — Princeton, NJ: World Science Communications, 1973 . Первоначальные публи-
кации: Lee, T. D., Yang, C. N. Question of Parity Conservation in Weak Interactions, // Physical
Review, 1956, 104, p . 254–258; Wu, C. S., Ambler, E., Hayward, R. W., Hoppes, D. D., Hudson, R. P .
Experimental Test of Parity Nonconservation in Beta Decay // Physical Review, 1957, 105,
p . 1413–1415 . В полном соответствии с опасениями Ву другие физики сумели очень быстро
воспроизвести достигнутый ею результат . Действительно, еще одна группа ученых Ко-
лумбийского университета поспешно провела эксперимент, подтвердивший правильность
первоначальных выводов, и их статья была опубликована немедленно после выхода рабо-
ты Ву и др . (Garwin, R. L., Lederman, L. L., Weinrich, M . Observation of the Failure of
Conservation of Parity and Charge Conjugation in Meson Decays: The Magnetic Moment of
the Free Muon // Physical Review, 1957, 105, p . 1415–1417) . 
198
Часть III . Энтропия и ось времени
20
21
Christenson, J. H., Cronin, J. W., Fitch, V. L., Turlay, R. Evidence for the 2π Decay of the K20
Meson // Physical Review Letters, 1964, 13, p . 138–140 . В стандартной модели физики эле-
ментарных частиц существует общепринятый способ учета нарушения CP-инвариантности,
разработанный Макото Кобаяси и Тосихидэ Масукава (Kobayashi, M., and Maskawa, T. CP-
Violation in the Renormalizable Theory of Weak Interaction // Progress of Theoretical Physics
49 (1973): 652–57), которые обобщили идею Николы Кабиббо . Кобаяси и Масукава
удостоились Нобелевской премии в 2008 году .
Здесь мы также делаем пару предположений: во-первых, мы считаем, что физические
законы инвариантны относительно сдвига по времени (то есть не меняются от одного
момента к другому), а во-вторых, что они детерминированы (будущее можно пред-
сказать абсолютно точно, а не просто с какой-то вероятностью) . Если любое из этих
предположений оказывается неверным, то определение, является ли интересующий нас
набор законов инвариантным относительно направления времени, становится несколь-
ко сложнее . 
Гл а в а 8
Энтропия и беспорядок
Никому не дано представить в телесных об-
разах обращение времени . Время необратимо .
Владимир Набоков.
Смотри на арлекинов!
Почему обсуждения энтропии и второго начала термодинамики так часто за-
канчиваются разговорами о еде? Вот несколько популярных (и вкусных) при-
меров, когда энтропия увеличивается в ходе необратимых процессов:
‹
‹
‹
‹
‹
вы разбиваете яйца и готовите яичницу;
смешиваете кофе с молоком;
проливаете вино на новый ковер;
вынимаете пирог из духовки, и его аромат распространяется по квартире;
кидаете кубики льда в стакан воды, и они постепенно тают .
Честно говоря, не все эти примеры одинаково аппетитны; тот, что с кубиком
льда, пресноват, — хотя это легко исправить, заменив воду джином . Кроме того,
пример с приготовлением яичницы требует дополнительного разъяснения . На
самом деле приготовление яиц нельзя считать прямолинейной демонстрацией
второго начала термодинамики . Готовка — химическая реакция, вызываемая
нагреванием, и этот процесс не был бы возможен, если бы яйца не были от-
крытыми системами . Энтропия вступает в игру, когда мы разбиваем яйца
и перемешиваем белки с желтками; смысл тепловой обработки получившейся
смеси в том, чтобы избежать отравления сальмонеллой, а не продемонстриро-
вать принципы термодинамики .
Взаимоотношения между энтропией и едой основываются по большей
части на таком вездесущем процессе, как смешивание . На кухне мы очень часто
именно этим и занимаемся — смешиваем два вещества, которые до этого су-
ществовали сами по себе или хранились раздельно . Это могут быть как две
разные формы одной и той же субстанции (лед и жидкая вода), так и два со-
вершенно разных ингредиента (молоко и кофе, белки и желтки яиц) . Перво-
проходцы термодинамики были чрезвычайно заинтересованы в изучении
влияния тепла на различные объекты из повседневной жизни, и таяние кубика
льда стало бы для них проблемой первоочередной важности . Куда меньшее
любопытство у них вызвали бы процессы, в которых принимают участие
200
Часть III . Энтропия и ось времени
ингредиенты, имеющие одинаковую температуру, например пролитое на ковер
вино . Однако совершенно очевидно, что независимо от температуры между
всеми этими процессами есть нечто сходное: изначально субстанции разъеди-
нены, а в конечном состоянии перемешаны между собой . Смешать вещи очень
легко, а вот разъединить куда труднее . Стрела времени накладывает свой от-
печаток на все, что мы делаем на кухне .
Почему смешивать ингредиенты легко, а отделять их друг от друга сложно?
Когда мы смешиваем две жидкости, мы видим, как разноцветные завихрения
постепенно сливаются, образуя равномерно окрашенную текстуру . Это зрели-
ще не слишком помогает разобраться, что именно там происходит . Так что
давайте вместо этого рассмотрим смешивание песка двух разных цветов . Важ-
но то, что песок состоит из дискретных частей — отдельных песчинок . Это ни
у кого не вызывает сомнения . Смешивая, например, синий песок с красным,
мы получаем песок фиолетового цвета . Но это не означает, что каждая песчин-
ка из обеих порций окрасилась в фиолетовый цвет . Песчинки сохраняют ин-
дивидуальность — синие остаются синими, а красные красными; они просто
беспорядочно перемешиваются . Только если мы глядим издалека («макроско-
пически») смесь кажется однообразно фиолетовой; если приглядеться (по-
смотреть на нее «микроскопически»), мы увидим те же самые синие и красные
песчинки .
Одним из величайших достижений пионеров кинетической теории — Да-
ниила Бернулли из Швейцарии, Рудольфа Клаузиуса из Германии, Джеймса
Клерка Максвелла и Уильяма Томсона из Великобритании, Людвига Больцма-
на из Австрии и Джозайи Уилларда Гиббса из США — было то, что они пер-
выми стали рассматривать все жидкости и газы так, как мы только что описы-
вали песок: как наборы крохотных кусочков, сохраняющих свои отличительные
черты . Разумеется, мы не ищем в жидкостях и газах песчинки; мы знаем, что
они сделаны из атомов и молекул . Однако принцип остается неизменным .
Когда мы наливаем молоко в кофе, не происходит никакого чудесного объеди-
нения отдельных молекул молока с отдельными молекулами кофе, и молекулы
нового вида не появляются в этой смеси . Два набора молекул просто переме-
шиваются . Даже тепло — это свойство атомов и молекул, а не какая-то отдель-
ная самостоятельная жидкость . Теплота объекта — характеристика энергии
быстро движущихся молекул, из которых он состоит . Когда кубик льда тает
в стакане воды, молекулы не меняются . Они всего лишь сталкиваются друг
с другом, вследствие чего их энергия равномерно распределяется между всеми
молекулами, содержащимися в стакане . 
Глава 8 . Энтропия и беспорядок
201
Не давая (пока что) точного математического определения энтропии, на
примере смешивания песка двух цветов мы можем показать, что перемешивать
вещи значительно проще, чем разделять их обратно . Представьте себе миску,
в которую насыпали песок: все синие песчинки находятся у одного бортика,
а все красные у противоположного . Очевидно, что эта конфигурация доста-
точно специальная: если потрясти миску или помешать содержимое ложкой,
то красный песок начнет смешиваться с синим . Если же с самого начала на-
сыпать в миску смесь двух типов песка, то конфигурация будет устойчива:
сколько ни перемешивай, менее разнородной смесь не станет . Причина про-
ста: для того чтобы разделить два типа песка, нам потребуется применить
намного более точное действие, чем простое потряхивание или перемеши-
вание . Нам придется взять увеличительное стекло и аккуратно порабо-
тать пинцетом, перенося красные песчинки к одному бортику миски, а си-
ние к другому . Для создания нестабильного специального состояния
необходимо вкладывать куда больше труда, чем для создания стабильной
неразберихи .
Все то же самое можно изложить с ужасающе научной количественной
точки зрения — что Больцман и другие, собственно говоря, и сделали
в 1870-х годах . Мы тщательно изучим результаты их работы и попробуем
понять, на какие вопросы они дают ответы, а на какие нет и насколько эти
ответы согласуются с основополагающими законами физики, которые, как
мы знаем, полностью обратимы . Однако уже сейчас должно быть понятно,
что ключевую роль здесь играет большое количество атомов, составляющих
макроскопические объекты в реальном мире . Если бы у нас была только одна
красная песчинка и одна синяя, то между «смешанным» и «несмешанным»
состояниями никакого различия бы не было . В предыдущей главе мы говори-
ли о том, что физические законы работают совершенно одинаково как вперед
во времени, так и назад (при условии, что мы дали надлежащее определение
направлению времени) . Это микроскопическое описание, требующее тща-
тельного отслеживания каждой индивидуальной составляющей системы .
Однако в реальном мире, где в различных процессах участвует невообразимое
количество атомов, мы попросту не в состоянии обрабатывать такие объемы
информации . Нам приходится прибегать к упрощениям — рассматривать
средний цвет, или температуру, или давление вместо положения и импульса
каждого атома . Когда мы мыслим макроскопически, мы забываем (или от-
брасываем) детальную информацию об отдельных частицах, — и здесь на
сцену выходят энтропия и необратимость . 
202
Часть III . Энтропия и ось времени
Огрубление
Главное, что мы хотим понять, — это «как макроскопические характеристики
системы, состоящей из множества атомов, меняются вследствие движения от-
дельных атомов?» (Я буду попеременно использовать все три термина — «ато-
мы», «молекулы» и «частицы», подразумевая примерно одно и то же, так как
для нас важно лишь то, что это крохотные объекты, подчиняющиеся обратимым
законам физики, и что для того, чтобы сконструировать нечто макроскопиче-
ское, нужно взять необычайно много таких объектов .) Чтобы разобраться
в этом, рассмотрим герметичный контейнер, разделенный на две части пере-
городкой, в которой проделано отверстие . Молекулы газа летают в одной по-
ловине контейнера и чаще всего отскакивают от центральной перегородки,
однако периодически часть молекул пролетает сквозь отверстие на другую
половину . Можно предположить, например, что молекулы отскакивают от
перегородки в 995 случаях из 1000, но полпроцента из них при каждом стол-
кновении (которое случается, скажем, каждую секунду) умудряется пробрать-
ся в другую часть контейнера .
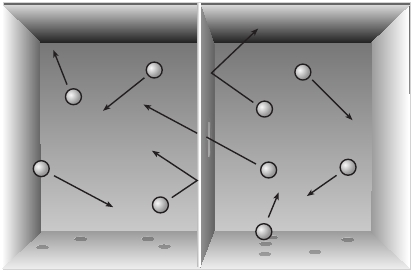
Рис . 8 .1 . Контейнер, полный молекул газа, посередине которого установлена перегородка
с отверстием . Каждую секунду у каждой молекулы есть крошечный шанс пролететь сквозь
отверстие на другую сторону 
|
Глава 8 . Энтропия и беспорядок
203
Этот пример весьма специфичен и тем удобен; мы можем в деталях изучить
каждый вариант развития событий и описать, что при этом происходит .1 Про
каждую молекулу в левой половине контейнера мы можем сказать, что каждую
секунду с вероятностью 99,5 % она останется в своей половине, а с вероятно-
стью 0,5 % переместится в противоположную; то же самое верно для правой
половины контейнера . Это правило абсолютно инвариантно относительно
обращения времени: если снять на пленку движение произвольной частицы,
подчиняющейся этому правилу, то при просмотре фильма невозможно будет
сказать, вперед или назад по времени воспроизводится запись . На уровне от-
дельных частиц прошлое и будущее совершенно идентичны .
На рис . 8 .2 мы изобразили один из возможных вариантов; как всегда,
значение времени увеличивается снизу вверх . В контейнере 2000 «молекул
воздуха», и в момент времени t = 1 в левой части находится 1600 молекул,
а в правой — только 400 . (Пока что вы не должны спрашивать, почему перво-
начальная конфигурация выбрана именно такой, хотя позже, когда мы заменим
«контейнер» на «Вселенную», мы начнем задавать подобные вопросы .)
Итак, мы наблюдаем за молекулами, летающими внутри контейнера и отска-
кивающими от стенок, и то, что происходит далее, нас совсем не удивляет .
Каждую секунду любая молекула с небольшой вероятностью может перелететь
на другую половину, но поскольку в самом начале в одной части контейнера
существенно больше молекул, чем в другой, в целом наблюдается тенденция
к выравниванию . (В точности как с температурами в формулировке второго
начала термодинамики, предложенной Клаузиусом .) Пока в левой части
контейнера молекул больше, общее количество молекул, пролетающих сквозь
отверстие слева направо, превышает количество молекул, перемещающихся
в обратном направлении . Через 50 секунд мы увидим, что количества молекул
в обеих частях начинают выравниваться, а через 200 секунд они станут прак-
тически равными .
Очевидно, что этот контейнер — еще одна иллюстрация существования
стрелы времени . Даже если бы мы не указали моменты времени на различных
конфигурациях, показанных на рисунке, большинство людей без труда угадали
бы, что было в начале, а чем все закончилось . Нас не удивляет тот факт, что
концентрация молекул воздуха выравнивается, но мы бы были поражены, если
бы все (или почти все) молекулы внезапно собрались в одной половине кон-
тейнера . «Прошлое» — это с той стороны стрелы времени, где объекты на-
ходятся в более разделенном состоянии, тогда как «будущее» — это там, где
они перемешались, а их концентрация выровнялась . То же самое происходит,
когда вы наливаете в чашку кофе ложку молока и две жидкости смешиваются . 
204
Часть III . Энтропия и ось времени
t = 200
t = 50
t =1
Рис . 8 .2 . Поведение 2000 молекул газа в контейнере с перегородкой . В самом начале 1600 мо-
лекул находятся в левой части контейнера и 400 молекул — в правой . Через 50 секунд
в левой половине остается около 1400 молекул, а в правой их число уже составляет 600 .
По истечении 200 секунд молекулы равномерно распределены между двумя половинами
контейнера
Конечно же, это всего лишь статистическая картина, а не абсолютная
действительность . Я хочу сказать, что вполне вероятна ситуация, когда вна-
чале слева и справа в контейнере будет одинаковое число молекул, а потом
по удивительному стечению обстоятельств большинство частиц соберется
в какой-то одной половине, образовав очень неравномерное распределение .
Как мы увидим далее, вероятность такого исхода невелика, и чем больше 
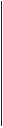







|
|
|
Глава 8 . Энтропия и беспорядок
205
частиц участвуют в процессе, тем она ниже; тем не менее нельзя сбрасывать
ее со счетов . Однако пока что мы можем смело игнорировать такие редкие
события и сконцентрироваться на наиболее вероятном варианте эволюции
системы .
Энтропия по Больцману
Нам хотелось бы сделать нечто большее, чем просто заявить: «Вполне очевид-
но, что молекулы, скорее всего, будут перемещаться до тех пор, пока равно-
мерно не распределятся по объему» . Мы хотели бы уметь обосновывать это
ожидание и заменять выражения типа «скорее всего» и «равномерно рас-
пределятся» строгими количественными характеристиками . Этим занимается
раздел науки под названием «статистическая механика» . Повторяя бессмерт-
ные слова Питера Венкмана: «С дороги, человек, я ученый!»
Первой крупной догадкой Больцмана было осознание того факта, что у мо-
лекул есть гораздо больше способов равномерно (более или менее) распреде-
литься по объему контейнера, чем всем вместе скопиться у одной из его стенок .
Представьте себе, что мы подсчитали имеющиеся молекулы и навесили на них
номера от 1 до 2000 . Нам интересно, сколько существует способов организовать
молекулы так, чтобы в левой и правой половинах контейнера оказалось ровно
требуемое число молекул . Например, сколько есть способов поместить 2000 мо-
лекул в левую часть и 0 в правую? Ровно один . Мы следим только за тем, в какой
половине контейнера находится каждая молекула, и нас не интересуют ее
точное положение и импульс, поэтому мы всего лишь берем и помещаем каждую
молекулу в левую часть контейнера .
Теперь попробуем ответить на вопрос: сколькими способами можно по-
делить молекулы так, чтобы в левой части оказалось 1999 молекул, а в правой —
ровно одна? Ответ: двумя тысячами способов, по одному на каждую молекулу,
которой посчастливилось попасть в правую половину . А если мы хотим, чтобы
в правой части всегда находилась пара молекул? Это можно сделать 1 999 000 спо-
собов . И в конце концов, если мы обнаглеем поместить в правую половину три
молекулы, оставляя в левой 1997, то обнаружим, что вариантов такого разме-
щения молекул целых 1 331 334 000 .2
Очевидно, что эти числа увеличиваются очень быстро: 2000 намного
больше 1, 1 999 000 намного больше 2000, а 1 331 334 000 еще больше . По
мере того как мы в ходе своего мысленного эксперимента перемещаем все
больше и больше молекул в правую половину, опустошая левую, они продол-
жают возрастать, а затем в определенный момент начинают уменьшаться . 
206
Часть III . Энтропия и ось времени
В конце концов, задавшись вопросом, много ли существует способов поме-
стить все 2000 молекул в правую часть контейнера, оставив в левой ровно
ноль, мы вновь вернемся к единственному уникальному варианту такой
конфигурации .
Ситуация, соответствующая наибольшему числу всевозможных конфигу-
раций, — очевидно, та, когда в каждой половине контейнера находится ровно
по 1000 молекул . Создать такую конфигурацию можно . . . в общем, очень боль-
шим количеством способов . Мы не будем приводить точное число; скажем
только, что оно примерно равно 2 ∙ 10600 — двойка, за которой следует шестьсот
нулей . И это всего лишь для двух тысяч частиц . Попробуйте вообразить при-
близительное число возможных конфигураций атомов в комнате с обычным
объемом воздуха или даже в стакане воды (предмет, который можно удержать
в руке, состоит где-то из 6 ∙ 1023 молекул — это число Авогадро) . Возраст Все-
ленной — всего лишь около 4 ∙ 1017 секунд, так что можете представить себе,
как быстро вам придется двигать молекулы туда и сюда, для того чтобы изучить
все возможные допустимые конфигурации .
Все это наводит на определенные мысли . Существует относительно не-
много способов собрать все молекулы в одной половине контейнера, но
огромное число вариантов более или менее равномерного распределения их
по доступному пространству . К тому же разумно ожидать, что очень неравно-
мерное распределение с легкостью будет переходить в относительно равно-
мерное, но не наоборот . Эти заявления похожи, но не эквивалентны . Следу-
ющим шагом Больцмана было предположение о том, что если у нас нет
какой-то особой информации о состоянии системы, то следует предполагать,
что она будет переходить от «специальных» конфигураций к «общим», то
есть от ситуаций, соответствующих относительно небольшому числу вари-
антов расположения частиц, к ситуациям, соответствующим множеству
способов их расположения .
Размышляя подобным образом, Больцман ставил целью объяснить на
атомном уровне второе начало термодинамики — утверждение, что энтропия
в замкнутой системе всегда увеличивается (или остается постоянной) . Фор-
мулировки второго начала уже были даны Клаузиусом и другими учеными,
однако Больцман хотел вывести их из некоего простого набора базовых
принципов . Вы уже заметили, что статистическое мышление движет нас
в правильном направлении: заявление о том, что «развитие систем проис-
ходит от специальных конфигураций к общим», весьма похоже на «развитие
систем происходит от конфигураций с низкой энтропией к конфигурациям
с высокой энтропией» . 
Глава 8 . Энтропия и беспорядок
207
Таким образом, напрашивается определение энтропии как «количества
перестановок микроскопических частей системы, при которых ее макроско-
пическое состояние не меняется» . В нашем примере с перегородкой внутри
контейнера это соответствует количеству способов разместить отдельные
молекулы внутри сосуда так, чтобы общее число молекул в каждой половине
осталось неизменным .
Мы почти подобрались к верному ответу, но все же не совсем . В действи-
тельности пионерам термодинамики было известно об энтропии не только то,
что «она обычно увеличивается» . Например, они знали, что если взять две
разные системы и заставить их взаимодействовать, то общая энтропия будет
равна простой сумме отдельных энтропий этих двух систем . Энтропия адди-
тивна, точно так же, как число частиц (в отличие, например, от температуры) .
Однако количество конфигураций совершенно точно свойством аддитивности
не обладает: если соединить два контейнера с газом, то общее количество
способов реорганизации молекул в двух контейнерах станет во много раз
больше, чем в пределах одной емкости .
Больцману удалось справиться с задачей формулировки определения эн-
тропии в терминах микроскопических перестановок . Мы будем использовать
букву W (от немецкого Wahrscheinlichkeit — «вероятность») для обозначения
количества перестановок микроскопических составляющих системы без из-
менения ее макроскопических свойств . Последним шагом Больцмана было
взятие логарифма от W и объявление о том, что результат пропорционален
энтропии .
Слово «логарифм» звучит очень по-научному, но это всего лишь способ
показать, как много цифр понадобится для написания числа . Если число пред-
ставляет собой степень 10, то его логарифм равен всего лишь этой степени,3 то
есть логарифм 10 равен 1, логарифм 100 равен 2, логарифм 1 000 000 равен
6 и т . д .
В приложении мы более подробно обсудим некоторые математические
тонкости . Они не очень важны для составления глобальной картины; если вы
притворитесь, что не замечаете слова «логарифм», то ничего особо не поте-
ряете . В действительности важно знать только лишь две вещи:
‹
‹
по мере увеличения чисел возрастают и их логарифмы;
но не слишком быстро; сами числа становятся неимоверно больше, однако
их логарифмы увеличиваются довольно медленно . Один миллиард намного
больше тысячи, однако 9 (логарифм миллиарда) не сильно больше 3 (лога-
рифм 1000) . 
208
Часть III . Энтропия и ось времени
Когда дело доходит до огромных чисел, например таких, с которыми мы
сталкиваемся в этой игре, последнее свойство здорово нам помогает . Поделить
2000 частиц поровну можно 2∙10600 способов — просто невообразимое число!
Но логарифм этого числа равен всего лишь 600,3 — с этим еще можно иметь
дело .
Формула Больцмана для энтропии, традиционно обозначаемой буквой S
(букву E мы использовать не хотим, потому что она обычно обозначает энер-
гию), гласит, что энтропия равна произведению некоторой константы k, кото-
рая называется постоянной Больцмана, на логарифм W, где W — число микро-
скопических состояний системы, неразличимых с макроскопической точки
зрения .4 Таким образом5,
S = k lg W .
Это, без сомнения, одно из важнейших уравнений за всю историю науки —
триумф физики XIX века, которое можно поставить в один ряд с ньютоновским
описанием динамики в XVII веке и революционными открытиями в области
теории относительности и квантовой механики в двадцатом . Посетив могилу
Больцмана в Вене, вы увидите, что это уравнение выгравировано на его над-
гробном камне (см . главу 2) .6
Взятие логарифма избавляет нас от основной проблемы, а формула Больц-
мана приводит как раз к тем свойствам, которые разумно ожидать от такого
явления, как энтропия . В частности, полная энтропия двух систем после
объединения равна всего лишь сумме энтропий этих систем . Это обманчиво
простое уравнение обеспечивает количественную связь между микроскопи-
ческим миром атомов и макроскопическим миром, который мы видим вокруг
себя .7