Для начала вообразим один-единственный бильярдный шар, катающийся по
столу (распространить правила игры сразу на несколько шаров будет совсем
нетрудно) . Мы считаем, что он никогда не теряет энергию и, наталкиваясь на
бортик, просто отскакивает . В целях нашей задачи «идеальный отскок» будет
частью «физических законов» данной замкнутой системы — бильярдного
шара . Так что же можно считать состоянием этого единственного шара?
На первый взгляд кажется, что логично считать состоянием шара в любой
момент времени его положение на столе . В конце концов, если сделать фото-
графию стола, то что мы увидим? Место, где в тот момент находился шар . Од-
нако выше мы определили состояние как полную информацию, требуемую для
предсказания движения системы; очевидно, что одного лишь положения нам
недостаточно . Если я скажу, что шар находится точно в центре стола (и больше
ничего), и попрошу вас предсказать, где он окажется секундой позже, то вы не
сможете дать мне точный ответ, ведь вам неизвестно, в какую сторону шар
катился .
Разумеется, для предсказания движения шара на основании информации,
имеющейся в наличии в конкретный момент времени, нам нужно знать как
положение, так и скорость объекта . Говоря «состояние шара», мы имеем
в виду его положение и скорость и — обратите внимание! — ничего более .
Нам неважно, например, с каким ускорением шар катится, какое сейчас вре-
мя суток, чем шар позавтракал в этот день и что еще происходит в его вну-
треннем мире .
Для описания движения частиц в классической механике вместо скорости
часто используют такое понятие, как импульс . История данного понятия вос-
ходит к тысячному году и связана с величайшим персидским философом Ибн
Синой (в латинизированном написании Авиценна) . Он предложил теорию
движения, в которой «влечение» — произведение массы и скорости — оста-
ется в отсутствие внешних воздействий постоянным . Импульс сообщает нам,
какой энергией обладает объект и в каком направлении он движется .13 В нью-
тоновской механике импульс равен произведению массы на скорость, а в теории
относительности формула слегка модифицируется с учетом того, что с при-
ближением скорости объекта к скорости света его импульс возрастает до бес-
конечности . Если вам известен импульс объекта с фиксированной массой, то
вы знаете его скорость, и наоборот . Следовательно, определить состояние
любой частицы можно, указав ее положение и импульс . 
178
Часть III . Энтропия и ось времени
t =1
t =2
t =0
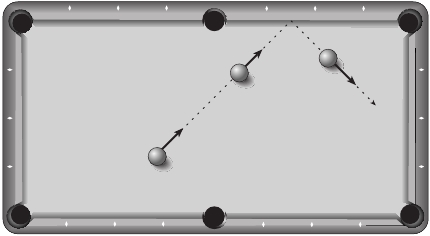
Рис . 7 .6 . Одинокий бильярдный шар, катающийся по столу без трения . Показаны состояния
в три разных момента времени . Стрелочки обозначают импульс шара; он остается постоян-
ным до тех пор, пока шар не отскочит от бортика
Зная положение и импульс бильярдного шара, вы можете полностью пред-
сказать всю траекторию, по которой он будет следовать, катаясь по столу . Пока
шар свободно катится, не касаясь стенок, импульс остается постоянным; ме-
няется лишь положение шара вдоль прямой линии, и происходит это с посто-
янной скоростью . Когда шар врезается в бортик, импульс мгновенно отража-
ется относительно линии бортика, после чего шар продолжает движение
с постоянной скоростью, то есть он отскакивает . Я описываю простые вещи
сложными словами, но это необходимо .
Вся суть ньютоновской механики в этом и заключается . Если по одному
и тому же столу катается много шаров, то полное состояние системы пред-
ставляет собой всего лишь набор положений и импульсов каждого из них .
Скажем, состояние Солнечной системы — это положения и импульсы всех
планет, а также Солнца . Или же, если вам хочется большей детальности и реа-
листичности, — то это положения и импульсы всех частиц, из которых состо-
ят эти объекты . А состояние вашего парня или девушки включает описание
положения и импульса каждого атома его или ее тела . Правила классической
механики позволяют однозначно предсказать, по какому пути пойдет развитие
системы, опираясь лишь на информацию о ее текущем состоянии . После того
как вы составили нужный список, дело берет в свои руки демон Лапласа, и ис-
ход предопределен . Однако вы не столь умны, как демон Лапласа, и у вас нет 
|
Глава 7 . Время, назад!
179
доступа к такому объему информации, поэтому парни и девушки навсегда
останутся загадками . Кроме того, они представляют собой открытые системы,
так что в любом случае вам потребовалась бы также информация и обо всем
остальном мире .
Во многих ситуациях удобно рассуждать обо «всех потенциально воз-
можных состояниях системы», называемых пространством состояний систе-
мы . Обратите внимание на то, что слово «пространство» употребляется
в двух, казалось бы, совершенно разных смыслах . У нас есть пространство —
физическая арена, на которой происходит движение реальных объектов во
Вселенной, а также абстрактное понятие пространства как математического
набора объектов (это почти то же самое, что и «множество», но с возмож-
ностью существования некой дополнительной структуры) . Пространство
состояний — это пространство, способное принимать разные формы в за-
висимости от рассматриваемых физических законов .
В ньютоновской механике пространство состояний называется фазовым
пространством, хотя причины такого именования не до конца ясны . Это
всего лишь набор всех возможных положений и импульсов всех присутству-
ющих в системе объектов . В мире шахматных досок пространство состояний
состоит из всевозможных последовательностей белых и серых квадратиков
в одной строке, а также может включать некоторую дополнительную инфор-
мацию в точках, где пересекаются диагональные линии . Когда мы окунемся
в квантовую механику, то столкнемся с пространством состояний, состоящим
из всех возможных волновых функций, описывающих квантовую систему; на
техническом языке это называется гильбертовым пространством . В любой
уважающей себя физической теории присутствует пространство состояний
и правила, описывающие эволюцию конкретных состояний с течением вре-
мени .
У пространства состояний может быть громадное количество измерений,
даже если обычное пространство всего лишь трехмерное . В этом контексте под
измерением понимается «число, необходимое для фиксации точки в простран-
стве» . В пространстве состояний есть по одному измерению для каждой
компоненты положения и по одному измерению для каждой компоненты
импульса для каждой частицы в системе . Если мы говорим о бильярдном шаре,
катающемся по плоскому двумерному столу, то нам требуется два числа для
описания его положения (так как сам стол двумерный) и два числа для описания
его импульса (величины и направления) . Таким образом, пространство состо-
яний одного бильярдного шара, привязанного к двумерному столу, четырех-
мерное: два числа для положения, два для импульса . 
180
Часть III . Энтропия и ось времени
(
)
}
(«
»)
(
-
)
(
;
)
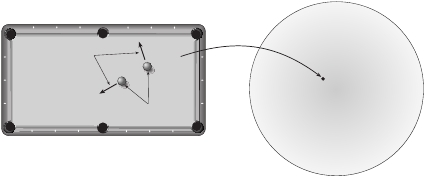
Рис . 7 .7 . Два шара на бильярдном столе и соответствующее пространство состояний . Для
обозначения положения каждого шара на столе требуется два числа, и еще два числа опи-
сывают его импульс . Полное состояние двух частиц представляет собой точку в восьмимер-
ном пространстве (справа) . Мы не можем нарисовать восемь измерений, так что постарай-
тесь вообразить, что они там действительно присутствуют . Каждый дополнительный шар
добавляет к пространству состояний четыре измерения
Если бы на столе было девять шаров, то нам потребовалось бы по два числа
на положение каждого шара и по два на их импульсы — итого тридцать шесть
измерений фазового пространства . Число измерений, требующихся для опи-
сания импульса и положения, всегда совпадает, так как в реальном пространстве
вдоль каждой из осей пространства направлено по одной компоненте импуль-
са . Если рассмотреть случай бейсбольного мяча, летящего в воздухе, что экви-
валентно задаче об одной частице, свободно движущейся в трехмерном про-
странстве, то пространство состояний для него будет шестимерным . Для
1000 частиц оно будет 6000-мерным .
В реалистичных задачах пространство состояний чрезвычайно велико . На-
стоящий бильярдный шар состоит примерно из 1025 атомов, а пространство
состояний представляет собой список положений и импульсов каждого из них .
Вместо того чтобы рассматривать эволюцию всех этих атомов, движущихся
сквозь трехмерное пространство со своими импульсами, мы можем с равным
успехом говорить о движении всей системы целиком как об одной точке (со-
стоянии), движущейся сквозь пространство состояний с громадным количе-
ством измерений . Это кардинальный способ перепаковки огромного объема
информации в другую форму; нисколько не упрощая описание (мы всего лишь
подменили огромное количество частиц огромным количеством измерений),
он позволяет взглянуть на вещи с новой точки зрения . 
|
Глава 7 . Время, назад!
181
Ньютоновская механика инвариантна относительно выбора направления
времени . Если вы снимете фильм о том, как наш одинокий бильярдный шар
катается по зеленому фетру и отскакивает от бортиков стола, то ни один зритель
не сможет сказать, смотрит он эту пленку в прямом или в обратном воспроиз-
ведении . В обоих случаях на экране происходит одно и то же: шар катится по
прямой линии с постоянной скоростью до тех пор, пока не врежется в бортик
и не отскочит от него .
Однако это далеко не конец истории . В нашем шахматном мире мы опре-
делили инвариантность относительно обращения времени как идею о том, что
последовательность состояний системы можно отразить во времени, и резуль-
тат все так же будет подчиняться сформулированным для этого мира законам
физики . На шахматной доске состоянием является строка белых и серых ква-
дратиков; для бильярдного шара это точка в пространстве состояний, задающая
положение и импульс шара .
Взгляните на первую часть траектории шара на рис . 7 .6 . Шар равномерно
и прямолинейно катится вверх и вправо, величина его импульса остается по-
стоянной, и направлен импульс также вверх и вправо . Если зеркально отразить
происходящее во времени, то мы получим последовательность положений
шара, движущегося из верхней правой области стола в нижнюю левую,
а также набор одинаковых импульсов, указывающих вверх и вправо . Но это
какое-то безумие . Если шар катится вдоль траектории с обратным направле-
нием времени — сверху и справа вниз и влево, то и направление его импуль-
са должно совпадать с направлением скорости . Очевидно, что самый простой
рецепт — взять исходный набор состояний, упорядоченный во времени,
и воспроизвести его в неизменном виде в обратную сторону — не работает .
Получившаяся траектория не отвечает законам физики . (Совершенно оче-
видно, что импульс никак не может быть направлен в сторону, противо-
положную направлению скорости, ведь он равен произведению скорости
и массы!14)
Эта дилемма хоть и кажется неразрешимой, в действительности довольно
проста . В классической механике мы можем определить операцию обращения
времени не просто как воспроизведение исходного набора состояний в об-
ратную сторону, но как составную операцию, включающую изменение направ-
ления импульсов на противоположное. И тогда действительно классическая ме-
ханика окажется идеально инвариантной относительно обращения времени .
Если вы предоставите мне описание эволюции системы с течением времени,
включающее положения и импульсы каждой ее части в каждый момент време-
ни, то я смогу развернуть эти импульсы в обратную сторону, воспроизвести 
182
Часть III . Энтропия и ось времени
последовательность в обратном порядке и получить новую траекторию, кото-
рая также будет представлять собой правильное решение ньютоновских урав-
нений движения .
Это более или менее отвечает здравому смыслу . Возьмем планету, вращаю-
щуюся вокруг Солнца . Предположим, что вам стало интересно, как этот процесс
будет выглядеть в «обратной перемотке», — вы мысленно меняете направле-
ние течения времени, и теперь планета движется по той же орбите, но в об-
ратную сторону . Наблюдая эту картину в течение какого-то времени, вы при-
ходите к выводу, что все выглядит вполне достоверно . Это происходит потому,
что ваш мозг автоматически меняет направление импульса на противополож-
ное, — вам даже не приходится задумываться об этом, в вашем воображении
планета совершенно естественным образом движется в обратную сторону . Мы
не придаем этому большого значения, потому что не можем увидеть импульс
так же, как видим положение . Тем не менее это такая же важная часть состояния
любой системы, как и положение входящих в нее частиц .
Следовательно, нельзя говорить, что ньютоновская механика инвариантна
относительно самого тривиального определения обращения времени: взять
упорядоченную по времени допустимую последовательность состояний, по-
менять порядок их следования на обратный и посмотреть, будет ли новая по-
следовательность отвечать действующим законам физики . При этом никого
это особо не волнует . Мы просто даем более усовершенствованное определе-
ние: в этой упорядоченной во времени допустимой последовательности со-
стояний нужно преобразовать каждое индивидуальное состояние некоторым
простым, но конкретным способом и только после этого менять порядок сле-
дования состояний на обратный . Под «преобразованием» мы понимаем всего
лишь изменение каждого состояния согласно заранее согласованному правилу;
в случае ньютоновской механики требуемой трансформацией будет «измене-
ние направления импульса на обратное» . Если мы найдем достаточно простой
способ преобразования отдельных состояний, обеспечивающий соблюдение
законов физики даже после обращения времени, то сможем с гордостью объ-
явить, что эти законы инварианты относительно изменения направления
времени .
Это заставляет вспомнить (по крайней мере должно заставлять, если мой
план удался) диагональные линии с шахматной доски C . Там мы обнаружили,
что показанный на панели C' результат простого зеркального отражения упо-
рядоченной по времени последовательности состояний не отвечает правилам
исходного шаблона . Следовательно, шахматная доска C не допускает тривиаль-
ного обращения времени . При этом если сначала отразить шахматную доску 
Глава 7 . Время, назад!
183
по горизонтали и только после этого поменять направление времени, то ре-
зультат будет удовлетворять первоначальным правилам . Таким образом, в этом
мире существует хорошо определенная процедура преобразования индивиду-
альных состояний (строк, состоящих из квадратиков), показывающая, что
шахматная доска C инвариантна относительно обращения времени, но в более
изощренном смысле .
Понятие об обращении времени, включающее преобразование состояний
в дополнение к непосредственному изменению направления времени, может
вызывать сомнения, но физики постоянно занимаются чем-то подобным . На-
пример, в теории электричества и магнетизма при обращении времени элек-
трическое поле остается неизменным, а направление магнитного поля меняет-
ся . Это всего лишь часть требуемого преобразования; прежде чем пускать
время в обратную сторону, изменениям должны быть подвергнуты как магнит-
ное поле, так и импульс .15
Урок, который мы должны извлечь из всего этого, заключается в следующем .
Фраза «данная теория инвариантна относительно обращения времени» не
означает «можно только лишь поменять направление времени, и теория как
работала, так и продолжит работать» . На самом деле все немного сложнее:
нужно каким-то простым способом преобразовать состояние в каждый момент
времени, а потом уже менять направление времени, и тогда теория продолжит
работать, как раньше . Очевидно, что выражения типа «каким-то простым
способом» в определениях фундаментальных физических понятий несколько
подрывают их авторитет . Кто вправе судить, что можно считать достаточно
«простым», а что нет?
В действительности это не так уж важно . Если существует какое-то пре-
образование, которое можно применить к состоянию некой системы в каж-
дой момент времени так, чтобы движение «назад во времени» подчинялось
исходным физическим законам, вы можете смело объявлять это инвариант-
ностью относительно изменения направления времени . Или другим видом
симметрии, связанным с обращением времени, но не в точности равным ему .
Название не играет роли; важно лишь понимание всевозможных симметрий
и того, соблюдаются они рассматриваемыми законами или нет . В стандарт-
ной модели физики элементарных частиц действительно существует преоб-
разование состояний, после которого они могут быть «прокручены назад
во времени» так, чтобы исходные уравнения движения по-прежнему соблю-
дались . Но физики предпочитают не называть это «инвариантностью от-
носительно изменения направления времени» . Давайте посмотрим, как это
работает . 
184
Часть III . Энтропия и ось времени