Смысл игры в том, чтобы разгадать шаблон . Видя перед собой некий массив
квадратиков, вы должны выделить закономерности и описать шаблон, или
правила расстановки белых и серых квадратиков . После этого для проверки
вам покажут другие части доски, и вы сможете сравнить свои предположения
с фактическим расположением клеток . Последний шаг на языке игры называ-
ется «проверкой гипотезы» .
Разумеется, у этой игры есть и другое название: «наука» . Мы всего лишь
описали, что делают настоящие ученые для понимания природы, — только
в сильно идеализированном контексте . В случае физики хорошая теория вклю-
чает три ингредиента: характеристики объектов, из которых сделана Вселенная, 
Глава 7 . Время, назад!
169
A
Рис . 7 .2 . Пример мира «шахматной доски» с простым шаблоном заливки
вертикальных столбцов
место действия, по которому распределены эти объекты, и правила, которым
подчиняется поведение объектов . К примеру, в качестве объектов могут вы-
ступать элементарные частицы или поля, местом действия можно считать че-
тырехмерное пространство—время, а правилами — законы физики . Мир
шахматной доски именно такой: в качестве объектов выступают биты (нули
и единицы, белые и серые квадратики), местом действия является сама шахмат-
ная доска, а правила — законы природы в этом игрушечном мире — это ша-
блоны, которые мы распознаем исходя из поведения квадратиков . Играя в эту
игру, мы ставим себя на место воображаемых физиков, живущих в одном из
подобных шахматных миров . Они проводят время, пытаясь разгадать законо-
мерности в композициях квадратиков и сформулировать глобальные законы
природы .6
На рис . 7 .2 изображен простейший пример игры, который мы будем на-
зывать «шахматная доска A» . Очевидно, что какой-то шаблон здесь присут-
ствует: квадратики раскрашены по определенной схеме . Можно сказать, что
«если взять любой произвольный столбец, то все квадратики в нем будут на-
ходиться в одном и том же состоянии» . Однако мы должны быть осторожны
и убедиться в том, что здесь случайно не затесались никакие другие шаблоны,
ведь если кто-то найдет больше шаблонов, чем мы, то мы проиграем, а нашим
соперникам достанется Нобелевская премия шахматного мира . Создается 




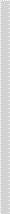













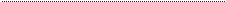



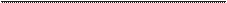


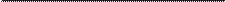
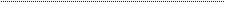

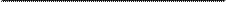




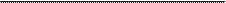


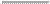






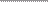


|
170
Часть III . Энтропия и ось времени
впечатление, что на шахматной доске A нет никаких
других очевидных шаблонов; мы пробежались глаза-
ми вдоль всей строки, но никаких идей, позволяющих
дополнительно упростить описание этого шахматно-
го мира, не возникло . Значит, мы закончили .
Каким бы простым этот пример ни казался, у шах-
матной доски A много общего с реальным миром .
Например, обратите внимание на то, что в найденном
нами шаблоне различаются «время» (направление
вверх по столбцам) и «пространство» (горизонталь-
ное направление вдоль строк ) . Различие между ними
состоит в том, что в строке может произойти все что
угодно; насколько мы можем судить, наличие инфор-
мации о состоянии одного конкретного квадратика
не позволяет сделать никаких выводов о состоянии
соседних . Аналогичным образом, в реальном мире мы
также можем стартовать с любой произвольной кон-
фигурации вещества в пространстве и предсказать,
что с этой конфигурацией будет происходить с тече-
Рис . 7 .3 . Физические за- нием времени, руководствуясь «законами физики» .
коны можно представлять Если у нас на коленях сидит кошка, то мы можем быть
себе как машину, которая уверены, что и мгновение спустя она будет где-то не-
исходя из текущего состо-
янии мира дает предска-
зание, каким мир станет
мгновением позже
Предположим, мы решили с нуля построить новую Вселенную . Кто сказал,
что в нашем творении между временем и пространством обязательно должно
существовать различие такого рода? Вполне возможно вообразить такой мир,
в котором вещи от момента к моменту будут меняться настолько же резко и не-
предсказуемо, как от места к месту . Однако в той Вселенной, где живем мы
с вами, данное различие действительно существует . Понятие времени, с ходом
которого вещи во Вселенной эволюционируют, не является логически неотъ-
емлемой частью мира; это всего лишь идея, которая внезапно оказывается
весьма удобной для размышлений о реальности, в которой мы живем .
Мы описали правило, действующее на шахматной доске A, так: «если взять
любой произвольный столбец, то все квадратики в нем будут находиться в од-
ном и том же состоянии» . Это глобальное описание, распространяющееся 



|
|
|
|
|
|
Глава 7 . Время, назад!
171
сразу же на весь столбец . Мы могли бы перефразировать его, сделав более ло-
кальным, чтобы можно было взять любую строку («момент во времени»)
и с помощью правила восстановить все остальные строки сверху или снизу .
Например, таким способом: «если мы знаем состояние любого конкретного
квадратика, то мы также знаем, что квадратик прямо над ним находится точно
в таком же состоянии» . Другими словами, мы описали шаблон в терминах раз-
вития с течением времени и теперь можем, начиная с какого-то конкретного
состояния в какой-то конкретный момент времени, продвигаться вперед (или
назад), восстанавливая состояние одной строки за раз . Это традиционный
способ применения законов физики к реальному миру, как показано на рис . 7 .3 .
Расскажите о состоянии всего мира (скажем, о положении и скорости каждой
частицы во Вселенной) в определенный момент времени, и законы физики
услужливо сообщат, каким мир станет мгновение спустя .7 Повторяя процесс,
можно построить полную картину будущего . А как насчет прошлого?
Ставя время с ног на голову
Для мира, существующего только в нашем воображении, шахматная доска уж
слишком однообразна и ограниченна . Невозможно представить, чтобы эти
маленькие квадратики могли закатить вечеринку или написать эпическую по-
эму . Тем не менее если бы на шахматных досках жили физики, то они нашли
бы, что обсудить после формулировки законов временной эволюции .
Физика шахматной доски A обладает определенной степенью симметрии,
например инвариантностью относительно сдвига по времени . Это означает,
что законы физики не меняются во времени от момента к моменту . Мы можем
сместить точку наблюдения вперед или назад во времени (вверх или вниз по
столбцам), но правило «квадратик прямо над текущим находится точно
в таком же состоянии» продолжит выполняться .8 Симметрии так и работают:
вы что-то делаете, но это ничего не меняет — правила продолжают действо-
вать, как и раньше . Мы уже говорили о том, что реальный мир также инвари-
антен относительно сдвига по времени: с течением времени законы физики
не меняются .
Кроме того, на шахматной доске A можно заметить еще один вид симме-
трии — инвариантность относительно обращения времени . Смысл такого вида
симметрии очевиден: мы заставляем время идти в обратную сторону и наблю-
даем за происходящим . Если результат «выглядит точно так же» — то есть
создается впечатление, что «перевернутая» система подчиняется тем же за-
конам физики, что и первоначальная расстановка, — то мы говорим, что дей- 
172
Часть III . Энтропия и ось времени
ствующие в системе правила инвариантны относительно обращения времени .
Для того чтобы проверить это на шахматной доске, нужно зеркально отразить
ее, выбрав осью симметрии какую-нибудь строку . При условии, что действую-
щие на шахматной доске правила также инвариантны относительно сдвига по
времени, совершенно неважно, какую строку мы выберем, так как они все
равны . Если правила, с помощью которых мы описывали исходную расстанов-
ку, так же действуют в новом шаблоне, то можно утверждать, что шахматная
доска инвариантна относительно обращения времени . Очевидно, что образец A,
в котором каждый столбец содержит квадратики только одного цвета, облада-
ет данным типом инвариантности: отраженный шаблон не только подчиняет-
ся тем же правилам, он еще и стопроцентно совпадает с исходным .
Для того чтобы лучше прочувствовать идею, давайте рассмотрим более
интересный пример . На рис . 7 .4 показан еще один мир шахматной доски, обо-
значенный B . Теперь мы видим два разных шаблона размещения серых квадра-
тиков: диагональные линии, идущие в обоих направлениях (получившийся
рисунок немного напоминает световые конусы, не правда ли?) . И снова мы
можем описать получившуюся схему размещения серых и белых квадратиков
в терминах развития от одного момента времени к следующему . Нужно только
не забывать о том, что в каждой конкретной строке нам недостаточно отсле-
живать цвет одного-единственного квадратика . Мы обязаны следить за тем,
какие типы диагональных линий из серых квадратиков проходят через эту
точку (и проходят ли вообще) . Каждую клетку можно пометить одним из че-
тырех состояний: «белая», «диагональная линия серых квадратиков проходит
вверх и вправо», «диагональная линия серых квадратиков проходит вверх
и влево», «диагональная линия серых квадратиков проходит в обе стороны» .
Если мы опишем любую произвольную строку всего лишь как последователь-
ность нулей и единиц, этого будет недостаточно, чтобы понять, как будет вы-
глядеть следующая строка .9 Все выглядит так, будто мы обнаружили в рассма-
триваемой Вселенной два типа «частиц»: одни движутся всегда только налево,
а другие — только направо, причем частицы разных типов никак не взаимодей-
ствуют между собой и не влияют друг на друга .
Что произойдет с шахматной доской B, если мы поменяем направление
времени на обратное? Суть этого шахматного мира останется прежней, одна-
ко фактическое расположение белых и серых квадратиков, разумеется, изме-
нится (в отличие от шахматной доски A, где вне зависимости от направления
времени мы получали один и тот же набор белых и серых клеток) . На второй
панели рис . 7 .4, обозначенной B', показан результат зеркального отражения
относительно одной из строк шахматной доски B . В частности, диагональные 
Глава 7 . Время, назад!
173
Рис . 7 .4 . Шахматная доска B (слева) характеризуется чуть более сложной динамикой, чем
шахматная доска A: в этом примере диагональные линии, состоящие из серых квадратиков,
следуют в обоих направлениях . Шахматная доска B' (справа) иллюстрирует результат об-
ращения времени на доске B относительно центральной строки
линии, проходившие из левого нижнего угла в правый верхний, теперь про-
тянулись из левого верхнего в правый нижний, и наоборот .
Инвариантен ли мир шахматной доски из примера B относительно обра-
щения времени? Определенно, это так . Пусть изменение направления времени
относительно произвольно выбранной строки и меняет индивидуальное рас-
пределение белых и серых клеток — это не важно . Важно то, что неизменными
остаются «законы физики», то есть правила, которым подчиняются схемы
закрашивания квадратиков . В исходном примере B, до изменения направления
времени, правила гласили, что существуют два типа диагональных линий, со-
держащих серые клетки . То же самое верно и для B' . И пусть два типа линий
обмениваются личинами; это не отменяет того факта, что как в состоянии «до»,
так и в состоянии «после» мы наблюдаем одни и те же два типа линий . Таким
образом, воображаемые физики из мира шахматной доски B объявили бы, что
законы природы инвариантны относительно изменения направления времени .
В Зазеркалье
Ну что, рассмотрим еще один мир шахматной доски? Теперь это будет шах-
матная доска C, показанная на рис . 7 .5 . И снова действующие в этом мире
правила кажутся довольно простыми: мы видим только диагональные линии, 

|
|
|
|
174
Часть III . Энтропия и ось времени
Рис . 7 .5 . В шахматном мире C присутствуют только диагональные линии серых квадратиков,
идущие из левого нижнего угла в правый верхний . Если изменить направление времени на
противоположное, то мы получим картинку C', на которой нет ничего, кроме диагональных
линий из правого нижнего угла в левый верхний . Строго говоря, шахматная доска C не
инвариантна относительно изменения направления времени — она инвариантна относи-
тельно одновременного отражения в пространстве и во времени
протянувшиеся из левого нижнего угла в правый верхний . Попробуем сфор-
мулировать правило «предсказания будущего» в терминах пошагового раз-
вития: «если мы знаем состояние любого конкретного квадратика, то мы
также знаем, что квадратик на один шаг выше и правее него находится в том
же самом состоянии» . Определенно, данное правило инвариантно относи-
тельно переноса во времени, так как результат его применения абсолютно не
зависит от того, с какой строки мы начнем .
Если изменить направление времени на шахматной доске C на противопо-
ложное, то мы получим конфигурацию, показанную на рис . 7 .5 на доске C' .
Очевидно, что эта ситуация отличается от ситуации с B и B' . Правила, которым
подчиняются клетки на доске C', отличаются от правил на доске C: вместо диа-
гональных линий, идущих из левого нижнего угла в правый верхний, мы теперь
видим линии, идущие в другую сторону . Физики, живущие в мирах C и C',
сказали бы, что наблюдаемые ими законы природы не обладают симметрией
относительно обращения времени . Мы безошибочно различаем направления
«вперед во времени» и «назад во времени»: «вперед» — это то направление,
в котором диагональные линии движутся вправо . Какое направление назначить
«будущим» — решать нам, но как только выбор сделан, «прошлое» и «буду-
щее» идентифицируются однозначно . 
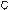

|
|
Глава 7 . Время, назад!
175
Однако это еще не конец истории . Хотя шахматная доска C, строго говоря,
не инвариантна относительно изменения направления времени (в том смысле,
как мы его определили), что-то «обратимое» в этом мире все же должно быть .
Давайте попробуем понять — что .
Помимо обращения времени, мы также могли бы рассмотреть вариант
«обращения» пространства . Для этого нам нужно отразить шахматную до-
ску по горизонтали относительно какого-то столбца . В реальном мире мы
получаем аналогичный результат, когда смотримся в зеркало, так что обраще-
нием пространства в данном случае можно считать обычное зеркальное от-
ражение . В физике это обычно называют преобразованием четности, которое
получается при одновременном обращении всех трех пространственных осей,
а не одной (как на шахматной доске) . Давайте тоже будем использовать этот
термин, чтобы у нас была возможность при необходимости сойти за настоя-
щих физиков .
Очевидно, что наша исходная шахматная доска A инвариантна относитель-
но преобразования четности: те правила поведения, которые мы на ней обна-
ружили, выполняются даже после горизонтального зеркального отражения .
В то же время на шахматной доске C мы сталкиваемся с ситуацией, аналогичной
той, которую мы получали, когда меняли направление времени на противопо-
ложное: четность — это не симметрия . Меняя «лево» на «право», мы пре-
вращаем мир с диагоналями «только вверх и вправо» в мир с диагоналями
«только вверх и влево» .
Тем не менее почему бы нам не взять шахматную доску C и не обратить
сразу и время и пространство? В получившемся мире будут действовать те же
правила, с которых все началось . При обращении времени первый тип диаго-
налей превращается во второй, а отражение в пространстве восстанавливает
исходную картинку . Все встает на свои места, а этот эксперимент иллюстри-
рует одну важную особенность изменения направления времени в фундамен-
тальной физике: очень часто бывает так, что определенная физическая теория
не инвариантна относительно «наивного инвертирования времени», при
котором меняется лишь направление времени и больше ничего . Однако та же
самая теория может быть инвариантной относительно некоторого правильно
обобщенного преобразования симметрии, которое не ограничивается лишь
обращением времени, а включает какие-то дополнительные преобразования .
В реальном мире это происходит по весьма изощренному сценарию, который
в изложении некоторых авторов учебников по физике становится еще сложнее
и запутаннее . Итак, давайте оставим наш дискретный мир шахматных досок
и бросим взгляд на настоящую Вселенную . 
176
Часть III . Энтропия и ось времени