Нормальная форма – это запись ЛФ в базисе И, ИЛИ, НЕ.
Запись булевой функции в СДНФ, заданной таблично, производится по следующему алгоритму:
· в таблице истинности выделяются строки, для которых значение функции равно единице;
· для выделенных строк записывают минтермы (конституенты 1), т. е. произведения аргументов, причем если какой-нибудь аргумент в строке равен нулю, то берется его отрицание;
· записывается логическая сумма полученных минтермов.
Представление булевой функции в СКНФ основано на понятии макстерма (конституенты 0).
Для записи булевой функции в СКНФ необходимо:
· в таблице истинности выделить строки, для которых значение функции равно нулю;
· для выделенных строк записывают макстермы, т. е. сумму аргументов, причем если какой-нибудь аргумент в строке равен единице, то берется его отрицание;
· записывается логическое произведение полученных макстремов.
Например, для функции неравнозначности y(x1, x2), заданной таблично (табл. 1.1), ее аналитическое представление будет иметь вид:
СДНФ 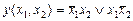 ,
,
СКНФ 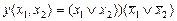 .
.
Таблица 1 .1
| Номер набора | x1 | x2 | y | Минтермы м i | Макстермы М i |
| 0 | 0 | 0 | 0 | 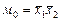
| 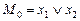
|
| 1 | 0 | 1 | 1 | 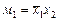
| 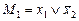
|
| 2 | 1 | 0 | 1 | 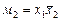
| 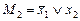
|
| 3 | 1 | 1 | 0 | 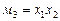
| 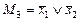
|
Булева функция, заданная таблично или аналитически, может быть изображена на карте Карно, представляющей собой прямоугольник, разбитый на 2m клеток, где m – число аргументов функции.
Если функция записана в СДНФ (наиболее употребляемой), то для отображения ее на карте Карно в клетки, «координаты» которых соответствуют минтермам, вписывают единицы, в остальные клетки записывают нули (и другие символы – для недоопределенных функций).
Если ЛФ задана в СКНФ, то в клетки карты Карно, соответствующие макстермам, вписывают нули, а в остальные – единицы и другие символы.
На рис. 1.2 показано отображение на картах Карно функции неравнозначности, заданной в СДНФ (а) и СКНФ (б).
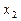
| 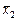
| 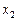
| 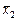
| |||
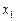
| 0 | 1 | 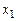
| 0 | 1 | |
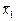
| 1 | 0 | 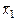
| 1 | 0 |
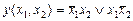
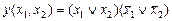
а б
Рис. 1.2
Минимизация булевых функций. Упрощение булевых функций или их минимизация – это нахождение из всех возможных форм представления ЛФ такой формы, при которой обеспечивается минимум целевой функции (аппаратных затрат, быстродействия, экономичности и т. д.). Из многочисленных методов минимизации на практике наибольшее распространение получили аналитический и минимизирующих карт.
Аналитический метод минимизации основан на использовании для упрощения заданной ЛФ аксиом и законов алгебры логики, алгоритма Квайна.
В процессе минимизации ЛФ, заданной в СДНФ, сначала находится сокращенная ДНФ (СкКНФ), затем она проверяется на лишние, не влияющие на истинность функции члены, и в результате получается тупиковая ДНФ (ТДНФ).
Если в испытуемой СкДНФ выявлено несколько лишних членов, то сразу их все исключать нельзя. В начале исключают один из избыточных членов, оставшееся выражение проверяют на лишние члены, в результате чего получают первую ТДНФ. Затем из СкДНФ удаляют второй лишний член, проводят испытание оставшихся членов, получают вторую ТДНФ и т. д. Таким образом, из всех полученных тупиковых форм можно выбрать минимальную ДНФ (МДНФ).
Метод минимизирующих карт основан на использовании карт Карно. Процесс минимизации сводится к заключению в контуры соседних клеток, содержащих единицы, и к считыванию с карты упрощенной функции.
Минимизированная ДНФ ЛФ представляет собой дизъюнкцию конъюнкций общих для каждого контура переменных. Число контуров должно быть минимальным, а их площадь максимальной. Площадь прямоугольника покрытия может быть Sпр.= 2m-i клеток, где i = {0, m} – целое число.
Если, например, m = 3, то возможно Sпр.= 1, 2, 4, 8.
В результате можно сразу получить тупиковую форму ЛФ.
На рис. 1.3 сплошными линиями показано оптимальное покрытие единиц, которое дает тупиковую форму исходной ЛФ в СДНФ 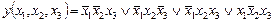 (таблица истинности – табл. 1.2) в виде
(таблица истинности – табл. 1.2) в виде 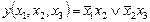 . Третий контур покрытия (пунктирный) соответствует члену
. Третий контур покрытия (пунктирный) соответствует члену 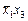 , который является лишним.
, который является лишним.
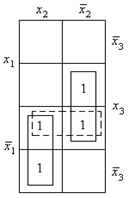
Рис. 1.3
Таблица 1.2
| Номер набора | x1 | x2 | x3 | y(x) |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 0 |
Опасные состязания в комбинационных схемах и способы их устранения. Под опасными состязаниями или гонками понимают нарушение заданного алгоритма функционирования логической схемы при смене входных наборов переменных, связанное с задержками сигналов в цепочках логических элементов.
При выявлении гонок обычно рассматривают соседние состояния (наборы), отличающиеся значением переменной только в одном разряде, так как одновременное изменение нескольких входных переменных может быть исключено методами противогоночного кодирования.
Различают статические и динамические состязания.
Статические состязания имеют место в случае, когда по алгоритму функционирования для двух соседних состояний значение ЛФ остается неизменным. Различают единичные и нулевые состязания.
Динамические состязания могут возникать при формировании на входе соседними состояниями алгоритмического перехода на выходе
от нуля к единице, и наоборот.
На практике больше внимания уделяют статическим состязаниям.
Для выявления опасных состязаний в логических схемах на практике используется критерий Хаффмена: статические состязания в устройстве с минимальной структурой имеют место, если на карте Карно при охвате соседних клеток контурами склеивания останутся хоты бы две клетки, не покрытые контуром.
В качестве примера выясним возможность появления опасных статических состязаний в цифровой логической схеме, реализующей функцию, МДНФ которой 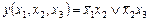 была найдена раньше.
была найдена раньше.
На карте Карно (рис. 1.2) имеются две соседние клетки с «координатами» 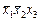 и
и 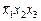 (переходы 1 « 3), не охваченные контуром покрытия единиц, и в соответствии с критерием Хаффмена в схеме могут появиться опасные 1-состязания. Их устранение достигается введением дополнительного контура покрытия (показан пунктиром), который оказался лишним при переходе от СкДНФ к ТДНФ.
(переходы 1 « 3), не охваченные контуром покрытия единиц, и в соответствии с критерием Хаффмена в схеме могут появиться опасные 1-состязания. Их устранение достигается введением дополнительного контура покрытия (показан пунктиром), который оказался лишним при переходе от СкДНФ к ТДНФ.
Для построения данной схемы на ЛЭ И–НЕ применим к ЛФ двойное отрицание и теорему де Моргана
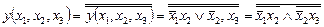 .
.
Полученная схема (рис. 1.4) не будет свободна от опасных 1-состязаний, но если ввести дополнительный ЛЭ И–НЕ (его подключение показано пунктиром), соответствующий третьему избыточному контуру покрытия единиц, то опасность появления гонок будет устранена.
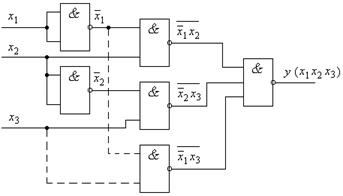
Рис. 1.4
Логическая функция с дополнительным ЛЭ примет вид
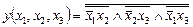 .
.
Идеализированные (без учета длительности фронтов) временные диаграммы, соответствующие переходам 1 « 3 (001 « 011), приведены на рис. 1.5. Пунктирными линиями и стрелками отмечены задержки сигналов в ЛЭ схемы. При переходе 1 ® 3 (001 ® 011) задержки не вызывают неалгоритмического перехода логической функции. Но при переходе 3 ® 1 (011 ® 001) в интервале Dt функция 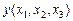 обращается в нуль, что противоречит таблице истинности (табл. 1.2). При подключении дополнительного ЛЭ на его выходе
обращается в нуль, что противоречит таблице истинности (табл. 1.2). При подключении дополнительного ЛЭ на его выходе 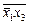 формируется уровень нуля, благодаря чему функция равна единице.
формируется уровень нуля, благодаря чему функция равна единице.
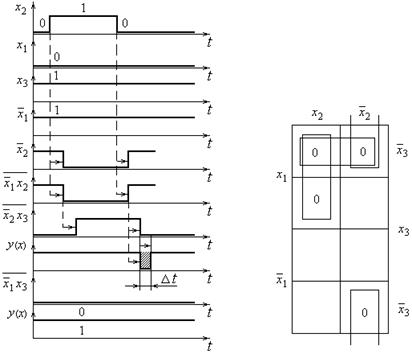
Рис. 1.5 Рис. 1.6
Для выявления опасных 0-состояний нужно перейти к покрытию на карте Карно нулей, что достигается инвертированием ЛФ и нанесением контуров и нулей в соответствии с выражением
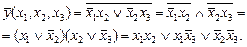
В этом случае (рис. 1.6) соседние клетки охвачены контурами покрытия и опасных 0-состязаний не будет. Таким образом, повышение функциональной надежности комбинационных логических схем достигается введением избыточных логических элементов, что усложняет схему и приводит к увеличению аппаратных затрат. На практике применяются и другие способы построения функционально-устойчивых схем: передача сигналов от одного устройства к другому с помощью специальных импульсов синхронизации, пауза между которыми выбирается такой, чтобы за ее время полностью закончились переходные процессы в ЛЭ и схемах.
Структурные схемы в отечественной литературе и документации логические элементы изображают прямоугольником (так называемое основное поле), в верхнем части которого указывают символ функции: & для И, 1 для ИЛИ. Входы показывают с левой стороны прямоугольника, выходы – с правой. Инверсные входы и выходы выделяются небольшим кружком у вывода.
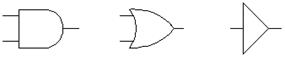
a b c
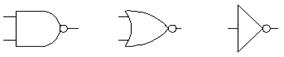
d e f
Рис. 1.7. Графические обозначения логических элементов
На рис. 1.7 показаны обозначения базовых логических элементов , принятые в программе EWB: a – элемент И (AND); b – элемент ИЛИ (OR); c – буферный логический элемент; d – элемент И-НЕ (NAND); e – элемент ИЛИ-НЕ (NOR); f – инвертор НЕ (NOT);
Для двухвходовых элементов можно увеличить количество входов до восьми, открывая двойным щелчком по значку компонента диалоговое окно «Number of inputs».
Моделирование логических схем в программе EWB целесообразно проводить с помощью логического преобразователя (ЛП).
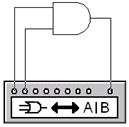
Рис.1.8. Схема для исследования логического элемента – И
На рис. 1.8 приведена схема логического преобразователя для исследования элемента – И. При наличии двух входов возможны только четыре комбинации входных сигналов, что отображается на экране преобразователя в виде таблицы истинности, которая генерируется после нажатия кнопки  . Для получения булева выражения исследуемого элемента необходимо нажать кнопку
. Для получения булева выражения исследуемого элемента необходимо нажать кнопку  . Для упрощения выражения следует нажать кнопку
. Для упрощения выражения следует нажать кнопку 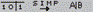 . Выражения приводятся на дополнительном дисплее, расположенном в нижней части лицевой панели. Причем логическое сложение отражается символом «+», отрицание – символом «'». При умножении двух аргументов они пишутся друг за другом без каких-либо символов. При нажатии кнопки
. Выражения приводятся на дополнительном дисплее, расположенном в нижней части лицевой панели. Причем логическое сложение отражается символом «+», отрицание – символом «'». При умножении двух аргументов они пишутся друг за другом без каких-либо символов. При нажатии кнопки  на рабочем поле EWB мы получаем схему, реализующую данную ЛФ в базисе И-ИЛИ-НЕ, а при нажатии кнопки
на рабочем поле EWB мы получаем схему, реализующую данную ЛФ в базисе И-ИЛИ-НЕ, а при нажатии кнопки  – схем в базисе И-НЕ. При работе с конвертором следует помнить, что самым старшим является разряд А, а самым младшим – разряд Н.
– схем в базисе И-НЕ. При работе с конвертором следует помнить, что самым старшим является разряд А, а самым младшим – разряд Н.
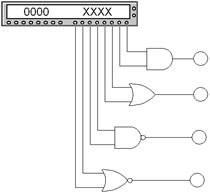
Рис. 1.9. Схема исследование логических элементов с
помощью генератора слова. Выходы логических элементов
подключены к светоиндикаторам логических уровней
ЛАБОРАТОРНОЕ ЗАДАНИЕ
1. Ознакомиться с программой моделирования “Electronics Work- bench” (EWB)5.12 Руководство пользователю) ”.
2. Установить экспериментально функциональную полноту ЛЭ ИЛИ–НЕ, И–НЕ выполнив на их основе логические схемы, реализующие операции НЕ, И, ИЛИ с помощью логического преобразователя (Л.П.) в EWB с помощью схемы на рис. 1.8 и установите для каждого из них соответствие таблицы истинности и булева выражения.
3. Синтезировать минимизированную функционально-устойчивую комбинационную логическую схему, алгоритм функционирования которой задан следующей таблицей истинности (табл. 1.3) (по вариантам):
Таблица 1.3
Варианты заданий
| Вариант | Функция алгебры логики | Вариант | Функция алгебры логики |
| 1. | 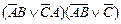
| 16. | 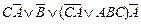
|
| 2. | 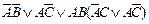
| 17. | 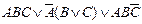
|
| 3. | 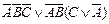
| 18. | 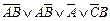
|
| 4. | 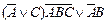
| 19. | 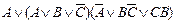
|
| 5. | 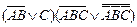
| 20. | 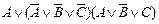
|
| 6. | 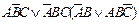
| 21. | 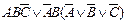
|
| 7. | 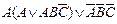
| 22. | 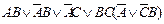
|
| 8. | 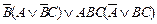
| 23. | 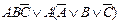
|
| 9. | 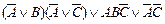
| 24. | 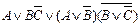
|
| 10. | 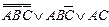
| 25. | 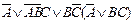
|
| 11. | 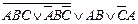
| 26. | 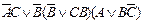
|
| 12. | 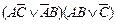
| 27. | 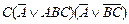
|
| 13. | 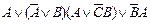
| 28. | 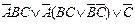
|
| 14. | 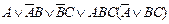
| 29. | 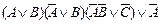
|
| 15. | 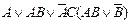
| 30. | 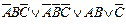
|
3.1. Построить при помощи программы EWB дискретную схему без ее упрощения по формуле, взятой из таблицы 1.3, в соответствии с заданным вариантом.
3.2. Получить таблицу истинности (ТИ) построенной схемы, используя ЛП.
3.3. По ТИ, используя соответствующее свойство ЛП, найти СДНФ.
3.4. На основе СДНФ построить схему дискретного устройства в базисе И-ИЛИ-НЕ и базисе И-НЕ.
3.5. Провести минимизацию ЛФ по карте Карно.
3.6. Пользуясь критерием Хаффмена, определить возможность появления статических опасных состязаний (единичных и нулевых), предложить меры для их устранения.
3.7. Построить свободную от статических опасных состязаний минимизированную функцию в базе И–НЕ используя ЛП, упростить СДНФ и построить схему дискретного устройства в базе И-НЕ и ИЛИ-НЕ
3.8. Сравнить схемы дискретного устройства пункта 3.1, 3.4, 3.7.
3.9. Нарисовать идеализированные временные диаграммы для опасных переходов входных сигналов.
Содержание отчета
Наименование и цель работы; краткие сведения из теории; полученные результаты на основании выполненного задания, а также результаты проведенных исследований схем, которые должны быть приведены в отчете вместе с описанием их работы; выводы по работе.








